Gamma function

The gamma function is a mathematical function that extends the domain of factorials to non-integers. The factorial of a positive integer n, written n!, is the product 1·2·3···n. The gamma function, denoted by $\Gamma$, is defined to satisfy $\Gamma (n)=(n-1)!$ for all positive integers n and to smoothly interpolate the factorial between the integers. The gamma function is one of the most commonly occurring examples of a nonelementary function; that is, a function that cannot be expressed in finite terms using algebraic operations, exponentials, and logarithms. Its study dates back to Leonhard Euler, who gave a formula for its calculation in 1729.

Motivation

It is easy to graphically interpolate the factorial to non-integer values, but is there a formula that describes the resulting curve?

Is there a "closed-form expression" for the product 1·2·3···n? To be in closed form, the number of arithmetic operations should not depend on the size of n. Such an expression would have several uses; first of all, we could calculate n! in a less tedious manner than by performing (n-1) multiplications. As a famous anecdote tells, Carl Friedrich Gauss found as a child that the sum $1+2+...+n$ can be written as $n(n+1)/2$ — and was thereby able to quickly sum all the integers between 1 and 100, to the astonishment of his teacher. But a closed-form expression has more benefits than just computational convenience. If a formula does not depend on the size of n, it is also irrelevant whether the n is precisely an integer, and the formula should work for fractional numbers. Gauss's formula for sums of consecutive integers (such sums are now called triangular numbers) is obviously valid for non-integer values of n — in fact, when plotted for a continuously changing variable n, it describes a parabola.

Does it at all make sense to define the factorial of a fraction? Whether or not such numbers are useful, it is easy to see that they could at least be defined. By plotting the factorial of a few small integers, it becomes apparent that the dots can be connected with a smooth curve. We could, very roughly, calculate fractional factorials by just inspecting the graph. The problem is that it is not so easy to find a formula that exactly describes the curve. In fact, we now know that no simple such formula exists — "simple" meaning that no finite combination of elementary functions such as the usual arithmetic operations and the exponential function will do. Considering the simple solution for triangular numbers, it may come as surprise that changing "+" to "·" makes such a difference. But it is possible to find a general formula for factorials, if we deploy tools from calculus. As it turns out, the idea of a fractional factorial makes a lot of sense.

Defining the gamma function

The problem of extending the factorial to non-integer arguments was apparently first considered by Daniel Bernoulli and Christian Goldbach in the 1720s, and was solved at the end of the same decade by the Swiss mathematician Leonhard Euler. The gamma function is commonly defined by a definite integral due to Euler,

$\Gamma (z)=\int _{0}^{\infty }e^{-t}t^{z-1}dt,$

where $t^{z-1}$ is interpreted as $e^{(z-1)\log t}$ if $z$ is not an integer. Using standard theorems from mathematical analysis, it can be shown that Euler's integral defines $\Gamma$ to be a continuous function if $z$ is positive, or indeed any complex number with positive real part. To see that it corresponds to the factorial at integers, we can insert $z+1$ instead of $z$ and perform an integration by parts to obtain

$\Gamma (z+1)=\left[-e^{-t}t^{z}\right]_{0}^{\infty }+z\int _{0}^{\infty }e^{-t}t^{z-1}dt=z\Gamma (z).$

This relation is called the recurrence formula or recurrence relation of the gamma function. The equation $f(z+1)=zf(z)$ is an example of a functional equation — an equation to be solved for the function $f$ for all values of $z$. It is analogous to the recurrence satisfied by factorials, $n!=n(n-1)!$, the only difference being that the function argument has been shifted by 1. A repeated application of the gamma function's recurrence formula gives

$\Gamma (z+n)=z(z+1)(z+2)\cdots (z+n-1)\Gamma (z),$

which together with the initial value $\textstyle \Gamma (1)=\int _{0}^{\infty }e^{-t}dt=1$ establishes that

$\Gamma (n)=1\cdot 2\cdot 3\ldots (n-1)=(n-1)!$

for positive integers $n$. We can of course equivalently write $\Gamma (n+1)=n!$. We may use these formulas to explicitly calculate $\Gamma (n)$ or, conversely, to define $z!$ for non-integers in terms of the gamma function.

Uniqueness

This establishes that it is possible to define a continuous extension of the factorial, but an important question needs to be addressed: is the gamma function as we have defined it the unique such extension? The answer is no: there are infinitely many ways to connect any discrete set of points with a smooth curve. Infinitely many solutions remain if we demand that $\Gamma (z+1)=z\Gamma (z)$ must hold for all numbers z, not just integers, so this extra criterion is not strong enough.

The pragmatic reason for using Euler's particular extension of the factorial is that his integral often turns up in applications, whereas other extensions do not.

The first page of Euler's paper "De progressionibus transcendentibus seu quarum termini generales algebraice dari nequeunt".

There is a complication, however: although Euler's function is arguably the most natural extension of the factorial, his integral is not the only formula that can be used to represent it. Other mathematicians who studied the gamma function have used different formulas as definitions, and although those formulas describe the same function, it is not entirely straightforward to prove the equivalence. Euler himself gave two different definitions: the first was not his integral but an infinite product,

$n!=\prod _{k=1}^{\infty }{\frac {\left(1+{\frac {1}{k}}\right)^{n}}{1+{\frac {n}{k}}}},$

of which he informed Goldbach in a letter dated October 13, 1729. He wrote to Goldbach again on January 8, 1730, to announce his discovery of the integral representation

$n!=\int _{0}^{1}(-\log s)^{n}\,ds,$

which is valid for $n>0$. By the change of varibles $t=-\log s$, this becomes the familiar Euler integral. Euler published his results in the paper "De progressionibus transcendentibus seu quarum termini generales algebraice dari nequeunt" ("On transcendental progressions, that is, those whose general terms cannot be given algebraically"), submitted to the St. Petersburg Academy on November 28, 1729.

A contemporary of Euler, James Stirling, also attempted to find a continuous expression for the factorial, using an entirely different approach. In his Methodus Differentialis (1730), he published the famous Stirling's formula

$n!\approx {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}$

Although Stirling's formula gives a good estimate of n!, also for non-integers, it does not provide the exact value. Stirling made several attempts to refine his approximation, and eventually found a solution, although he never managed to prove that the extended version of his formula indeed corresponds exactly to Euler's gamma function. A proof was first given by Charles Hermite in 1900.

A definite and generally applicable characterization of the gamma function was not given until 1922. Harald Bohr and Johannes Mollerup then proved what is known as the Bohr-Mollerup theorem: that the gamma function is the unique solution to the factorial recurrence relation that is also logarithmically convex for positive z. That is, if a function interpolates the factorial, and its logarithm is a convex function for positive $z$, it must be the gamma function. The gamma function is also uniquely defined for negative numbers, and everywhere else in the complex plane, since it can be shown to be an analytic function and analytic functions are uniquely defined by analytic continuation from any region of the complex plane.

The Bohr-Mollerup theorem is useful because it is relatively easy to prove logarithmic convexity for any of the different formulas used to define the gamma function. Taking things further, instead of defining the gamma function by any particular formula, we can choose the conditions of the Bohr-Mollerup theorem as the definition, and then pick any formula we like that satisfies the conditions as a starting point for studying the gamma function. This approach was used by the Bourbaki group.

Notation

The name gamma function and the symbol $\Gamma$ were introduced by Adrien-Marie Legendre around 1811; Legendre also rewrote Euler's integral definition in its modern form. Although the symbol is an upper-case Greek Gamma, there is no accepted standard for whether the function name should be written "Gamma function" or "gamma function" (some authors simply write "$\Gamma$-function"). The alternative "Pi function" notation $\Pi (z)=z!$ due to Gauss is sometimes encountered in older literature, but Legendre's notation is dominant in modern works.

It is justified to ask why we distinguish between the "ordinary factorial" and the gamma function by using distinct symbols, and particularly why the gamma function should be normalized to $\Gamma (n+1)=n!$ instead of simply using "$\Gamma (n)=n!$". Legendre's motivation for the normalization does not appear to be known, and has been criticized as cumbersome by some (the 20th-century mathematician Cornelius Lanczos, for example, called it "void of any rationality" and would instead use $z!$). The normalization does simplify some formulas, but complicates others.

Main properties

Real and complex numbers

The behavior of $\Gamma (z)$ for an increasing positive variable is simple: it grows quickly — faster than an exponential function, asymptotically as in Stirling's formula as $z\to \infty$.

The behavior for nonpositive $z$ is more intricate. Euler's integral is the most common form encountered for the gamma function in applications, but it does not converge for $z\leq 0$, so a product representation is more convenient in this case. One way is to use Euler's integral for positive arguments and extend the domain to negative numbers by repeated application of the recurrence formula,

$\Gamma (z)={\frac {\Gamma (z+n)}{z(z+1)\cdots (z+n-1)}},$

choosing $n$ such that $z+n$ is positive. Alternatively, we can start directly from either of the formulas

$\Gamma (z)=\lim _{m\to \infty }{\frac {m^{z}m!}{z(z+1)(z+2)\cdots (z+m)}}$

and

$\Gamma (z)={\frac {e^{-\gamma z}}{z}}\prod _{k=1}^{\infty }\left(1+{\frac {z}{k}}\right)^{-1}e^{z/k},\,\!$

where $\gamma \approx 0.577216$ is Euler's constant. Both representations can be derived from Euler's product representation by algebraic manipulation; the first was used by Gauss in 1811 and the second by Karl Weierstrass.

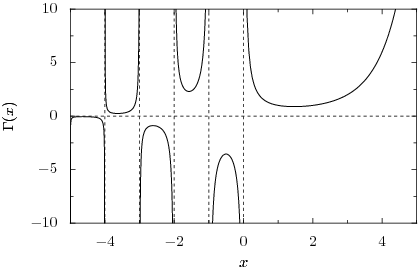
Whichever product we choose, we find that it contains a factor that blows up due to division by zero as $z$ approaches any of the integers $0,-1,-2,\ldots$. Thus, the gamma function must be undefined at those points; it is a meromorphic function with poles at the nonpositive integers. The following image shows the graph of the gamma function along the real line:

The gamma function is nonzero everywhere along the real line, although it comes arbitrarily close as $z\to -\infty$. There is in fact no complex number z for which $\Gamma (z)=0$, and hence the reciprocal gamma function $1/\Gamma$ is an entire function, with zeros at $z=0,-1,-2,\ldots$. We see that the gamma function has a local minimum at $x_{\mathrm {min} }\approx 1.46163$ where it attains the value $\Gamma (x_{\mathrm {min} })\approx 0.885603$. The gamma function must alternate sign between the poles because the product in the forward recurrence contains an odd number of negative factors if the number of poles between z and z+n is odd, and an even number if the number of poles is even.

Weierstrass originally wrote his product as one for $1/\Gamma$, in which case it is taken over the function's zeros rather than its poles. Inspired by this result, he proved what is known as the Weierstrass factorization theorem — that any entire function can be written as a product over its zeros; a generalization of the Fundamental Theorem of Algebra.

The gamma function on the real line

Interval	Sign	Local extreme xm	Γ(xm)
(0, ∞)	+	1.4616321449683623413	0.88560319441088870028
(-1, 0)	-	-0.50408300826445540926	-3.5446436111550050891
(-2, -1)	+	-1.5734984731623904588	2.3024072583396801358
(-3, -2)	-	-2.6107208684441446500	-0.88813635840124192010
(-4, -3)	+	-3.6352933664369010979	0.24512753983436625044

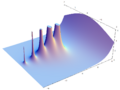
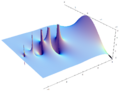
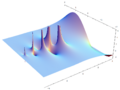
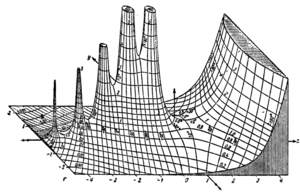
Although Euler was a pioneer in the theory of complex variables, he does not appear to have considered the factorial of a complex numbers, as instead Gauss first did. Plotting the gamma function in the complex plane yields beautiful graphs:

• 

  Absolute value

• 

  Real part

• 

  Imaginary part

Reflection, multiplication and rational arguments

The recurrence relation is not the only functional equation satisfied by the gamma function. Another important property is the reflection formula

$\Gamma (z)\Gamma (1-z)={\frac {\pi }{\sin \pi z}}$

which gives a concise relation between the gamma function of positive and negative numbers. The division by a sine, which is periodically zero, again indicates the existence of the gamma function's periodically occurring poles. Further, inserting z = 1/2 reveals the surprising fact that

$\Gamma (1/2)={\sqrt {\pi }}.$

Hence, by the recurrence formula, the gamma function or factorial of any half-integer is a rational multiple of ${\sqrt {\pi }}$. Both results were discovered by Euler, and are most easily derived by comparing his product representation with his product formula for the sine function. The value of $\Gamma (1/2)$ can also be calculated from Euler's integral, by changing variables to obtain a Gaussian integral.

A third functional equation is given by Gauss's multiplication theorem

$\prod _{n=0}^{k-1}\Gamma \left(z+{\frac {n}{k}}\right)=(2\pi )^{(k-1)/2}\;k^{1/2-kz}\;\Gamma (kz),$

of which Legendre's duplication formula

$\Gamma (z)\;\Gamma \left(z+{\frac {1}{2}}\right)=2^{1-2z}\;{\sqrt {\pi }}\;\Gamma (2z),\,\!$

is a special case.

It follows from the recurrence relation that $\Gamma (r+n)/\Gamma (r)$ is a rational function of $r$ whenever $n$ is an integer, and a rational number whenever $r$ is rational. From the multiplication formula, it is also possible to derive exotic-looking results such as

$2\pi ={\sqrt {3}}\;\Gamma \left({\begin{matrix}{\frac {1}{3}}\end{matrix}}\right)\Gamma \left({\begin{matrix}{\frac {2}{3}}\end{matrix}}\right)={\sqrt {2}}\;\Gamma \left({\begin{matrix}{\frac {1}{4}}\end{matrix}}\right)\Gamma \left({\begin{matrix}{\frac {3}{4}}\end{matrix}}\right).$

Given the curious appearance of ${\sqrt {\pi }}$ in the formula for the gamma function of half an integer, it may be tempting to look for a formula for other individual values $\Gamma (r)$ where $r$ is rational. However, these numbers are not known to be expressible in any simple way in terms of the elementary mathematical constants $\pi$ and $e$. It has been proved that $\Gamma (n+r)$ is algebraically independent of $\pi$ and itself a transcendental number for any integer $n$ and each of the fractions $r$ = 1/6, 1/4, 1/3, 2/3, 3/4, and 5/6; many more esoteric transcendence results are also known. Values of the gamma function at rational points have geometrical significance similar to that of $\pi$: they correspond to special values of elliptic integrals, which are used to calculate the circumference of ellipses ($\pi$, of course, comes from the special case of an ellipse with equal axes).

Derivatives

It is useful to think of the gamma function as the solution to its functional equations, particularly the recurrence relation. Most important special functions in applied mathematics arise as solutions to the continuous counterpart of recurrence relations: differential equations, which relate a function to its derivatives, but the gamma function does not appear to satisfy any simple differential equation. Otto Hölder proved in 1887 that the gamma function at least does not satisfy any algebraic differential equation by showing that a solution to such an equation could not satisfy the gamma function's recurrence formula. This result is known as Hölder's theorem.

Although the derivatives of the gamma function do not pop out of any simple differential equation, they exist and are analytic functions since the gamma function is analytic; they have been named polygamma functions. Polygamma functions at integers can be evaluated in terms of the Riemann zeta function, and hence the gamma function can be given a Taylor series expansion involving the zeta function around any integer.

Applications

Opening a random page in an advanced table of formulas, one may be as likely to spot a gamma function as a sine. One author describes the gamma function as "Arguably, the most common special function, or the least 'special' of them. The other transcendental functions listed below are called 'special' because you could conceivably avoid some of them by staying away from many specialized mathematical topics. On the other hand, the Gamma function $y=\Gamma (x)$ is most difficult to avoid."

Instead of attempting to give a comprehensive list of applications, we will now give a few prominent examples and identify some of the main reasons for the gamma function's frequent appearance.

Products involving the gamma function

The gamma function's ability to and generalize factorial products immediately leads to applications in many areas of mathematics; in combinatorics, and by extension in areas such as probability theory and the calculation of power series. Many expressions involving products of successive integers can be written as some combination of factorials, the most important example perhaps being that of the binomial coefficient

${n \choose k}={\frac {n!}{k!(n-k)!}}.$

We can replace the factorial by a gamma function to extend any such formula to the complex numbers. More generally, any product where each factor is a rational function of the index variable is susceptible to the same treatment. If $P$ and $Q$ are monic polynomials of degree $m$ and $n$ with respective roots $p_{1}\ldots p_{m}$ and $q_{1}\ldots q_{n}$, we have

$\prod _{i=a}^{b}{\frac {P(i)}{Q(i)}}=\left(\prod _{j=1}^{m}{\frac {\Gamma (b-p_{j}+1)}{\Gamma (a-p_{j})}}\right)\left(\prod _{k=1}^{n}{\frac {\Gamma (a-q_{k})}{\Gamma (b-q_{k}+1)}}\right).$

If we have a way to calculate the gamma function numerically, it is a breeze to calculate numerical values of such products. The number of gamma functions in the right-hand side depends only on the degree of the polynomials, so it does not matter whether $b-a$ equals 5 or $10^{5}$.

By taking limits, infinite products of rational functions can be evaluated in terms of the gamma function as well. Due to the Weierstrass factorization theorem, many simple analytic functions can be written as infinite products of rational factors, and hence can be represented as finite products or quotients of the gamma function. We have already seen one striking example: the reflection formula essentially represents the sine function as the product of two gamma functions. Starting from this formula, the exponential function as well as all the trigonometric and hyperbolic functions can be expressed in terms of the gamma function.

More functions yet, including the hypergeometric function and special cases thereof, can be represented by means of complex contour integrals of products and quotients of the gamma function, called Mellin-Barnes integrals.

Use in integration

A second reason for the gamma function's importance is that it permits close-form evaluation of many types of integrals that appear in both pure and applied mathematics.

As an elementary example, the gamma function is frequently useful when integrating a power of a function, $f(x)^{n}$. A strategy that sometimes works is to consider $n$ an integer, repeatedly integrate by parts to obtain an expression involving a factorial of $n$, and generalize with the gamma function to let $n$ be an arbitrary complex number.

Further, it is common to encounter integrals that can be rewritten as Euler's integral by a suitable change of variables. Many integral transforms involve multiplying a function by an exponential and integrating over the real line; for instance, the Laplace transform of the power function $f(t)=t^{c}$ is given by

${\mathcal {L}}\left\{f(t)\right\}=\int _{0}^{\infty }e^{-st}t^{c}\,dt={\frac {\Gamma (s+1)}{s^{c+1}}}.$

Such integrals also appear in the calculation of cumulative distribution functions and moment-generating functions in statistics; notably of the gamma distribution whose probability density function is given by

$g(t)={\frac {\lambda ^{\alpha }}{\Gamma (\alpha )}}e^{-\lambda t}t^{\alpha -1}\;\;(t\geq 0).$

The gamma function in front of the expression ensures that the cumulative density, generated by integrating $e^{-\lambda t}t^{\alpha -1}$, gets normalized to unity as $t\to \infty$. When choosing integration limits other than 0 and $\infty$, one obtains a generalization of the gamma function called an incomplete gamma function; there is also a multivariate gamma function that finds use in multivariate statistics.

Another commonly encountered generalization is the beta function

$\mathrm {\mathrm {B} } (x,y)={\frac {\Gamma (x)\,\Gamma (y)}{\Gamma (x+y)}}.$

Analytic number theory

The fact that the gamma function can be expanded in power series using the Riemann zeta function can be useful in the study of the gamma function, but a more important fact is that the gamma function can be used in the study of the zeta function. A fundamental property of the Riemann zeta function is its functional equation:

$\Gamma \left({\frac {s}{2}}\right)\zeta (s)\pi ^{-s/2}=\Gamma \left({\frac {1-s}{2}}\right)\zeta (1-s)\pi ^{(1-s)/2}.$

Among other things, this provides an explicit form for the analytic continuation of the zeta function to a meromorphic function in the complex plane and leads to an immediate proof that the zeta function has infinitely many so-called "trivial" zeros on the real line. Borwein et al. call this formula "one of the most beautiful findings in mathematics". Another champion for that title might be

$\zeta (z)\;\Gamma (z)=\int _{0}^{\infty }{\frac {t^{z-1}}{e^{t}-1}}\;dt.$

Both formulas were derived by Bernhard Riemann in his seminal 1859 paper "Über die Anzahl der Primzahlen unter einer gegebenen Grösse" ("On the Number of Prime Numbers less than a Given Quantity"), one of the milestones in the development of analytic number theory — the branch of mathematics that studies prime numbers using the tools of mathematical analysis. Factorial numbers, considered as discrete objects, are an important concept in classical number theory due to their compositeness properties, but Riemann found a use for their continuous extension that arguably turned out to be even more important.

Numerical calculation

Algorithms

It is a relatively convenient business to numerically calculate the gamma function for small arguments: given an approximation that holds on some interval of unit width, say for $1\leq z\leq 2$, or a complex strip with real part in such an interval, the value anywhere else can be computed easily via the recurrence and reflection formulas, using only a few multiplications or an evaluation of the sine in the reflection formula. In advanced numerical software that computes the gamma function with double precision (16 digits), the unit-interval approximation is usually an optimally chosen rational function, but for moderate precision an approximating polynomial works just as well. The gamma function can also be computed from any of several series representation, or even by direct numerical integration of Euler's integral, but either approach is generally less efficient than using a pre-computed approximation if a fixed precision is used.

For large arguments, say $|z|>10$, it is best to use an asymptotic expansion; the most popular is Stirling's series

$\Gamma (z+1)\sim {\sqrt {2\pi z}}\left({\frac {z}{e}}\right)^{z}\left(1+{\frac {1}{12z}}+{\frac {1}{288z^{2}}}-\cdots \right).$

This is Stirling's formula multiplied by a series that corrects the error. The series coefficients can be calculated in terms of Bernoulli numbers. The "$\sim$" sign denotes an asymptotic equality: the series diverges for every z, but yields arbitrarily accurate approximations of the gamma function as $z\to \infty$ if the series is truncated at the smallest term. We can use Stirling's series to calculate the gamma function for small numbers as well, using the recurrence relation. Taking $n=10$ and calculating $\Gamma (z)$ from $\Gamma (z+n)$, using the three first terms in Stirling's series, we obtain $\Gamma (1)$ ≈ 1.000003 and $\Gamma (2)$ ≈ 1.000002; this particular approximation is good to five decimal places on the interval $1\leq z\leq 2$. With larger $n$ and more terms, Stirling's series permits calculating the gamma function with arbitrary precision.

Other practical methods for high-precision calculation include the Lanczos approximation and Spouge's approximation, which are both similar in form to Stirling's series but have different convergence characteristics.

It should be noted that it may be convenient to work with the logarithm of the gamma function instead of the gamma function itself, since the raw gamma function grows quickly and can cause overflow in computer arithmetic. It is common to encounter a quotient of two large gamma function values, which is most safely computed by subtracting two logarithms. Stirling's, Lanczos's and Spouge's approximations can all be calculated directly in logarithmic form.

A hand-drawn graph of the absolute value of the complex gamma function, from Tables of Higher Functions by Jahnke and Emde.

Available software and tables

Double-precision floating-point implementations of the gamma function and its logarithm are available in most scientific computing software and special functions libraries, for example Matlab, GNU Octave, and the GNU Scientific Library. The gamma function was also added to the C mathematics library (math.h) as part of the C99 standard, but is not implemented by all C compilers. Arbitrary-precision implementations are available in most computer algebra systems, such as Mathematica and Maple. Pari/GP, MPFR and MPFUN contain free arbitrary-precision implementations.

Although the gamma function can be calculated virtually as easily as any mathematically simpler function with a modern computer — even with a programmable pocket calculator — this was of course not always the case. Until the mid-20th century, mathematicians relied on hand-made tables, notably a table computed by Gauss in 1813 and another by Legendre from 1825. Tables as well as hand-drawn graphs of the complex gamma function can be found in Tables of Higher Functions by Jahnke and Emde, first published in Germany in 1909.

There was in fact little practical need for anything but real values of the gamma function until the 1930s, when applications for the complex gamma function were discovered in theoretical physics. As electronic computers became available for the production of tables in the 1950s, several extensive tables for the complex gamma function were published to meet the demand, including a table accurate to 12 decimal places from the U.S. National Bureau of Standards.

Concluding remarks

The theory of the gamma function and its applications is rich enough to fill books — indeed, such books have been written. A recommended reading, although the book is now out of print, is Emil Artin's 38-page exposition The Gamma Function from 1931 (English translation from 1964). Artin, who argues that "the gamma function can be thought of as one of the elementary functions", develops the theory of the gamma function of a real variable in a thorough way using only elementary methods. Numerous books on the general topic of complex analysis devote a chapter to the gamma function, as does virtually every book on special functions.

The gamma function has caught the interest of some of the most prominent mathematicians of all time. Its history, researched for instance by P. J. Davis, reflects many of the major developments within mathematics since the 18th century. In the words of Davis, "each generation has found something of interest to say about the gamma function. Perhaps the next generation will also." The Nobel Prize-winning physicist Gerard 't Hooft, mentioning the gamma function, urges prospective students of physics to "enjoy studying its properties".