Fuzzy subset: Difference between revisions
imported>Giangiacomo Gerla |
imported>Giangiacomo Gerla |
||
| Line 17: | Line 17: | ||
=== Some set-theoretical notions for fuzzy subsets === | === Some set-theoretical notions for fuzzy subsets === | ||
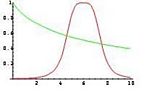
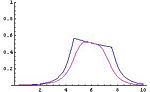
{{Image|Fuzzy2.JPG|right|150px|the intersection of the fuzzy subset of small number with the fuzzy subset of numbers close to 6 (obtained by the minimum and the product).}} | |||
In classical mathematics the definitions of union, intersection and complement are related with the interpretation of the basic logical connectives <math>\vee, \wedge, \neg</math>. In order to define the same operations for fuzzy subsets, we have to fix suitable operations <math> \oplus, \otimes</math> and ~ in [0,1] to interpret these connectives. Once this was done, we can set | In classical mathematics the definitions of union, intersection and complement are related with the interpretation of the basic logical connectives <math>\vee, \wedge, \neg</math>. In order to define the same operations for fuzzy subsets, we have to fix suitable operations <math> \oplus, \otimes</math> and ~ in [0,1] to interpret these connectives. Once this was done, we can set | ||
| Line 31: | Line 33: | ||
In such a case <math>([0,1]^F, \cup, \cap, -, \emptyset, S)</math> is a complete, completely distributive lattice with an involution. Several authors prefer to consider different operations, as an example to assume that <math>\otimes</math> is a [[triangular norm]] in [0,1] and that <math>\oplus </math> is the corresponding [[triangular co-norm]]. | In such a case <math>([0,1]^F, \cup, \cap, -, \emptyset, S)</math> is a complete, completely distributive lattice with an involution. Several authors prefer to consider different operations, as an example to assume that <math>\otimes</math> is a [[triangular norm]] in [0,1] and that <math>\oplus </math> is the corresponding [[triangular co-norm]]. | ||
For example, the picture represents the intersection of the fuzzy subset of small number with the fuzzy subset of numbers close to 6 obtained by the minimum and the product. | |||
In all the cases the interpretation of a logical connective is ''conservative'' in the sense that its restriction to {0,1} coincides with the classical one. This entails that the map associating any subset ''X'' of a set ''S'' with the related characteristic function is an embedding of the Boolean algebra <math>(\{0,1\}^S, \cup, \cap, -, \emptyset, S)</math> into the algebra <math>(L^S, \cup, \cap, -, \emptyset, S)</math>. | In all the cases the interpretation of a logical connective is ''conservative'' in the sense that its restriction to {0,1} coincides with the classical one. This entails that the map associating any subset ''X'' of a set ''S'' with the related characteristic function is an embedding of the Boolean algebra <math>(\{0,1\}^S, \cup, \cap, -, \emptyset, S)</math> into the algebra <math>(L^S, \cup, \cap, -, \emptyset, S)</math>. | ||
Revision as of 13:46, 5 January 2009
To be Completed !! Template:TOC-right
Introduction
The term fuzzy subset is a generalization of the subset concept from set theory. Observe that we can obtain a subset of a given set S by considering the extension of a well defined property P in S. Indeed, the axiom of comprehension reads that a subset B of S exists whose members are precisely those objects in S satisfying P. For example if S is the set of natural numbers and P is the property "to be prime", then the subset B of prime numbers is defined. Assume that P is a vague property as "to be big", "to be young": is there a way to define the extension of P ? For example:
- is there a precise definition of the notion of set of big numbers ?
The notion of fuzzy subset
An attempt to give an answer to such a question was proposed in 1965 by Lotfi Zadeh and at the same time, by Dieter Klaua in the framework of multi-valued logic. Now recall that the characteristic function of a classical subset X of S is the map cX : → {0,1} such that cX(x) = 1 if x is an element in X and cX(x) = 0 otherwise. Obviously, it is possible to identify every subset X with its characteristic function cX and therefore the extension of a property with a suitable characteristic function. This suggests that we can define the subset of big elements by a generalized characteristic function in which instead of the Boolean algebra {0,1} we can consider, for example, the interval [0,1]. The following is a precise definition.
Definition. Let S be a nonempty set, then a fuzzy subset of S is a map s from S into [0,1]. We denote by [0,1]S the class of all the fuzzy subsets of S. If S1,...Sn are nonempty sets then a fuzzy subset of S1×. . .×Sn is called an n-ary L-relation.
The elements in [0,1] are interpreted as truth values and, in accordance, for every x in S, the number s(x) is interpreted as the membership degree of x to s. We say that a fuzzy subset s is crisp if s(x) is in {0,1} for every x in S. By associating every classical subsets of S with its characteristic function, we can identify the subsets of S with the crisp fuzzy subsets. In particular we call "empty subset" of S the fuzzy subset of S constantly equal to 0. Notice that in such a way there is not a unique empty subsets.
Some set-theoretical notions for fuzzy subsets
In classical mathematics the definitions of union, intersection and complement are related with the interpretation of the basic logical connectives . In order to define the same operations for fuzzy subsets, we have to fix suitable operations and ~ in [0,1] to interpret these connectives. Once this was done, we can set
- ,
- ,
- .
In such a way an algebraic structure is defined and this structure is the direct power of the structure ~,0 ,1) with index set S. In Zadeh's original papers the operations , ~ are defined by setting for every x and y in [0,1]:
- = min(x, y) ; = max(x,y) ; = 1-x.
In such a case is a complete, completely distributive lattice with an involution. Several authors prefer to consider different operations, as an example to assume that is a triangular norm in [0,1] and that is the corresponding triangular co-norm. For example, the picture represents the intersection of the fuzzy subset of small number with the fuzzy subset of numbers close to 6 obtained by the minimum and the product. In all the cases the interpretation of a logical connective is conservative in the sense that its restriction to {0,1} coincides with the classical one. This entails that the map associating any subset X of a set S with the related characteristic function is an embedding of the Boolean algebra into the algebra .
L-subsets
The notion of fuzzy subset can be extended by substituting the interval [0,1] by any bounded lattice L. Again one assumes that in L suitable operations are defined to interpret the logical connectives. This extension was done mainly in the framework of fuzzy logic.
See also
- Fuzzy logic
- Fuzzy control system
- Neuro-fuzzy
- Fuzzy subalgebra
- Fuzzy associative matrix
- FuzzyCLIPS expert system
- Paradox of the heap
- Pattern recognition
- Rough set
Bibliography
- Cox E., The Fuzzy Systems Handbook (1994), ISBN 0-12-194270-8
- Elkan C.. The Paradoxical Success of Fuzzy Logic. November 1993. Available from Elkan's home page.
- Gerla G., Fuzzy logic: Mathematical Tools for Approximate Reasoning, Kluwer, 2001.
- Gottwald S., A treatase on Multi-Valued Logics, Research Studies Press LTD, Baldock 2001.
- Hájek P., Metamathematics of fuzzy logic. Kluwer 1998.
- Höppner F., Klawonn F., Kruse R. and Runkler T., Fuzzy Cluster Analysis (1999), ISBN 0-471-98864-2.
- Klaua D., Über einen Ansatz zur mehrwertigen Mengenlehre, Monatsberichte der Deutschen Akademie der Wissenschaften Berlin, vol 7 (1965), pp 859-867.
- Klir G. and Folger T., Fuzzy Sets, Uncertainty, and Information (1988), ISBN 0-13-345984-5.
- Klir G. , UTE H. St. Clair and Bo Yuan Fuzzy Set Theory Foundations and Applications,1997.
- Klir G. and Bo Yuan, Fuzzy Sets and Fuzzy Logic (1995) ISBN 0-13-101171-5
- Kosko B., Fuzzy Thinking: The New Science of Fuzzy Logic (1993), Hyperion. ISBN 0-7868-8021-X
- Novák V., Perfilieva I, Mockor J., Mathematical Principles of Fuzzy Logic, Kluwer Academic Publishers, Dordrecht, (1999).
- Yager R. and Filev D., Essentials of Fuzzy Modeling and Control (1994), ISBN 0-471-01761-2
- Zimmermann H., Fuzzy Set Theory and its Applications (2001), ISBN 0-7923-7435-5.
- Zadeh L.A., Fuzzy Sets, Information and Control, 8 (1965) 338-353.





![{\displaystyle ([0,1]^{S},\cup ,\cap ,-,\emptyset ,S)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2c3527a01030236ef22bc844e1d84e265470e6b)
![{\displaystyle ([0,1],\oplus ,\otimes ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a578615e200bb0fe3e715b9d50d32107f5ff5841)



![{\displaystyle ([0,1]^{F},\cup ,\cap ,-,\emptyset ,S)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8187875116d25b16cd1e44f84a9eb119a1446af)



