Legendre-Gauss Quadrature formula: Difference between revisions
imported>Dmitrii Kouznetsov (→Example: describe figure) |
imported>Gareth Leng No edit summary |
||
| Line 1: | Line 1: | ||
{{ | {{Subpages}} | ||
'''Legendre-Gauss Quadratude formiula''' is the approximation of the integral | '''Legendre-Gauss Quadratude formiula''' is the approximation of the integral | ||
:(1) <math>\int_{-1}^1 f(x)\,dx \approx \sum_{i=1}^N w_i f(x_i).</math> | :(1) <math>\int_{-1}^1 f(x)\,dx \approx \sum_{i=1}^N w_i f(x_i).</math> | ||
with special choice of nodes <math>x_i</math> and weights <math>w_i</math>, characterised in that, if the finction <math>f</math> is [[polynomial]] of order | with special choice of nodes <math>x_i</math> and weights <math>w_i</math>, characterised in that, if the finction <math>f</math> is [[polynomial]] of order smaller than <math>2N</math>, then the exact equality takes place in equation (1). | ||
Legendre-Gauss quadratude formula is special case of [[Gaussian quadratures]] of more general kind, which allow efficient approximation of a function with known asymptotic behavior at the edges of the interval of integration. | |||
==Nodes and weights== | ==Nodes and weights== | ||
Nodes <math>x_i</math> in equation (1) are zeros of the [[Polynomial of Legendre]] <math>P_N</math>: | Nodes <math>x_i</math> in equation (1) are zeros of the [[Polynomial of Legendre]] <math>P_N</math>: | ||
| Line 11: | Line 12: | ||
: (3) <math> -1<x_1<x_2< ... <x_N <1</math> | : (3) <math> -1<x_1<x_2< ... <x_N <1</math> | ||
Weight <math>w_i</math> in | Weight <math>w_i</math> in equation (1) can be expressed with | ||
: (4) <math> w_i = \frac{2}{\left( 1-x_i^2 \right) (P'_N(x_i))^2} </math> | : (4) <math> w_i = \frac{2}{\left( 1-x_i^2 \right) (P'_N(x_i))^2} </math> | ||
| Line 42: | Line 43: | ||
==Example== | ==Example== | ||
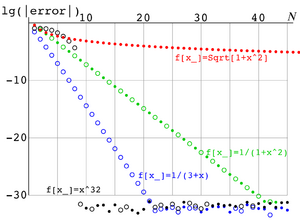
[[Image:GaulegExample.png|right|300px|thumb|Fig.1. Example of estimate of precision: Logarithm of residual versus number <math>N</math> of terms in the right hand side of equation (1) for various integrands <math>f(x)</math>.]] | [[Image:GaulegExample.png|right|300px|thumb|Fig.1. Example of estimate of precision: Logarithm of residual versus number <math>N</math> of terms in the right hand side of equation (1) for various integrands <math>f(x)</math>.]] | ||
In Fig.1, the [[decimal logarithm]] of the modulus of the residual of the appdoximation of integral with Gaussian quadrature is shown versus number of terms in the sum, for four examples of the integrand. | In Fig.1, the [[decimal logarithm]] of the modulus of the residual of the appdoximation of integral with Gaussian quadrature is shown versus number of terms in the sum, for four examples of the integrand. | ||
| Line 56: | Line 54: | ||
==Extension to other interval== | ==Extension to other interval== | ||
is straightforward. Should I copypast the obvious formulas here? | is straightforward. Should I copypast the obvious formulas here? | ||
==References== | ==References== | ||
<references/> | <references/> | ||
Revision as of 06:50, 24 January 2009
Legendre-Gauss Quadratude formiula is the approximation of the integral
- (1)
with special choice of nodes and weights , characterised in that, if the finction is polynomial of order smaller than , then the exact equality takes place in equation (1).
Legendre-Gauss quadratude formula is special case of Gaussian quadratures of more general kind, which allow efficient approximation of a function with known asymptotic behavior at the edges of the interval of integration.
Nodes and weights
Nodes in equation (1) are zeros of the Polynomial of Legendre :
- (2)
- (3)
Weight in equation (1) can be expressed with
- (4)
There is no straightforward espression for the nodes ; they can be approximated with many decimal digits through only few iterations, solving numerically equation (2) with initial approach
- (5)
These formulas are described in the books [1] [2]
Precision of the approximation
Example
In Fig.1, the decimal logarithm of the modulus of the residual of the appdoximation of integral with Gaussian quadrature is shown versus number of terms in the sum, for four examples of the integrand.
- (black)
- (red)
- (green)
- (blue)
The first of these functions is integrated "exactly" at , and the residual is determined by the rounding errors at the long double arithmetic. The second function (red) has branch points at the end of the interval; therefore, the approximation does not improve quickly at the increase of number terms in the sum. The last two functions are analytic within the range of integration; the residual decreases exponentially, and the precision of evaluation of the integral is limited only by the rounding errors.
Extension to other interval
is straightforward. Should I copypast the obvious formulas here?
References
- ↑ Abramovitz, Milton; I. Stegun (1964). Handbook of mathematical functions. National Bureau of Standards. ISBN 0-486-61272-4.
- ↑ W.H.Press, S.A.Teukolsky, W.T.Vetterling, B.P.Flannery (1988). Numerical Resipes in C. Cambridge University Press. ISBN 0-521-43108-5.