Legendre-Gauss Quadrature formula: Difference between revisions
imported>Dmitrii Kouznetsov (New. Fig.1 does not load as follows, problem with caption...) |
imported>Dmitrii Kouznetsov |
||
| Line 33: | Line 33: | ||
==Example== | ==Example== | ||
[[Image:GaulegExample.png|right| | <!-- | ||
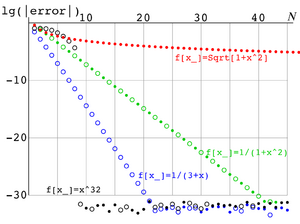
[[Image:GaulegExample.png|right|300px|thumb|Fig.1. Example of evaluation of integral (1) with different functions <math>f</math>, lg(|error|) versus number <math>N</math> of terms in the right hand side of equation (1).]] | |||
!--> | |||
[[Image:GaulegExample.png|right|300px|thumb|Fig.1. Example of estimate of precision: Logarithm of residual versus number <math>N</math> of terms in the right hand side of equation (1) for various integrands <math>f(x)</math>.]] | |||
==Extension to other interval== | ==Extension to other interval== | ||
is straightforward. Should I copypast the obvious formulas here? | is straightforward. Should I copypast the obvious formulas here? | ||
Revision as of 08:10, 27 May 2008
Template:Copyedit Legendre-Gauss Quadratude formiula is the approximation of the integral
- (1)
with special choice of nodes and weights , characterised in that, if the finction is polynomial of order smallet than , then the exact equality takes place in equation (1).
Legendre-Gauss quadratude formula is special case of Gaussian quadratures of more general kind, which allow efficient approximation of a function with known asumptiotic behavior at the edges of the interval of integration.
Nodes and weights
Nodes in equation (1) are zeros of the Polunomial of Lehendre :
- (2)
- (3)
Weight in equaiton (1) can be expressed with
- (4)
There is no straightforward espression for the nodes ; they can be approximated with many decimal digits through only few iterations, solving numerically equation (2) with initial approach
- (5)
These formulas are described in the books [1] [2]
Precision of the approximation
Example
Extension to other interval
is straightforward. Should I copypast the obvious formulas here?
References
- ↑ (1980) Handbook on special functions.
- ↑ Numerical Resipes in C. Do not forget to type data of the ref. here!.