imported>Paul Wormer |
imported>Paul Wormer |
| (41 intermediate revisions by the same user not shown) |
| Line 1: |
Line 1: |
| In [[molecular physics]], the '''Jahn-Teller effect''' is the distortion of a highly symmetric—but non-linear—[[molecule]] to lower symmetry and lower energy. The effect occurs if the molecule is in a degenerate state of definite energy, that is, if more than one [[wave function]] of the same energy is [[eigenfunction]] of the [[molecular Hamiltonian]]. When energy degeneracy of a molecular state arises—i.e., two or more orthogonal wave functions describe the same molecular state—the molecule will distort such that these wave functions will get different energies. By Jahn-Teller distortion, the molecule is lowered in symmetry and energy degeneracy is lifted. Some of the wave functions that have the same energy in the highly symmetric geometry obtain lower energy, while others obtain higher energy.
| | ==Parabolic mirror== |
| | {{Image|Refl parab.png|right|350px|Fig. 2. Reflection in a parabolic mirror}} |
| | Parabolic mirrors concentrate incoming vertical light beams in their focus. We show this. |
|
| |
|
| The effect is named after [[Hermann Arthur Jahn|H. A. Jahn]] and [[Edward Teller|E. Teller]] who predicted it in 1937.<ref>H. A. Jahn and E. Teller, ''Stability of Polyatomic Molecules in Degenerate Electronic States'', Proc. Royal Soc. vol. '''161''', pp. 220–235 (1937)</ref> It took some time before the effect was experimentally observed, because it was masked by other molecular interactions. However, there are now numerous unambiguous observations that agree well with theoretical predictions. These range from the excited states of the simplest non-linear molecule H<sub>3</sub>, through moderate sized organic molecules, like [[cation]]s of substituted [[benzene]], to [[transition metal]] complexes and localized impurity centers in solids.
| | Consider in figure 2 the arbitrary vertical light beam (blue, parallel to the ''y''-axis) that enters the parabola and hits it at point ''P'' = (''x''<sub>1</sub>, ''y''<sub>1</sub>). The parabola (red) has focus in point ''F''. The incoming beam is reflected at ''P'' obeying the well-known law: incidence angle is angle of reflection. The angles involved are with the line ''APT'' which is tangent to the parabola at point ''P''. It will be shown that the reflected beam passes through ''F''. |
|
| |
|
| <font style = "font-size: 85%; font-style: oblique; font-weight: bolder" >
| | Clearly ∠''BPT'' = ∠''QPA'' (they are vertically opposite angles). Further ∠''APQ'' = ∠''FPA'' because the triangles ''FPA'' and ''QPA'' are congruent and hence ∠''FPA'' = ∠''BPT''. |
| :The Jahn-Teller effect has a quantum mechanical origin and there is no classical-physics explanation of it. Therefore, some knowledge of quantum mechanics is prerequisite to the reading of this article. Further [[Schönflies]] notation for [[point group]]s and [[Mulliken]] notation for their irreducible representations is used. </font>
| |
| ==Explanation==
| |
| The Jahn-Teller effect is best explained by an example. Consider to that end the square homonuclear molecule in the middle of Fig. 1. Its symmetry group is D<sub>4h</sub>. Let there be two—in principle exact—electronic wave functions that together span the irreducible representation ''E''<sub>''u''</sub> of this group and assume that they describe the electronic state of the molecule. One wave function transforms as an ''x''-coordinate under D<sub>4h</sub> and is denoted by |''X'' ⟩. Its partner transforms as a ''y''-coordinate and is denoted by |''Y'' ⟩. In the case of the perfect square both wave functions have the same energy denoted by <math>\varepsilon_{E_u}</math>.
| |
|
| |
|
| To be more concrete, it may be helpful to mention that a simple approximate model for the wave functions is obtained from two degenerate [[molecular orbital]]s |''x''⟩ and |''y''⟩ (carrying ''E''<sub>''u''</sub>) that are outside a closed-shell and share a single unpaired electron. A closed-shell wave function (a many-electron wave function consisting of doubly occupied molecular orbitals) is invariant under the group operations. The wave function |''X'' ⟩ is modeled by the closed-shell wave function times orbital |''x''⟩ containing the electron, while |''Y'' ⟩ is modeled by the closed-shell wave function times molecular orbital |''y''⟩. The orbital |''x''⟩ transforming as an ''x''-coordinate has the ''yz''-plane—a mirror plane—as a nodal plane, that is, the orbital vanishes in this plane and has plus sign to the right and minus sign to the left of the plane. Similarly the orbital |''y''⟩ has the ''xz''-plane as a nodal plane.
| | We prove the congruence of the triangles: By the definition of the parabola the line segments ''FP'' and ''QP'' are of equal length, because the length of the latter segment is the distance of ''P'' to the directrix and the length of ''FP'' is the distance of ''P'' to the focus. The point ''F'' has the coordinates (0,''f'') and the point ''Q'' has the coordinates (''x''<sub>1</sub>, −''f''). The line segment ''FQ'' has the equation |
| | | :<math> |
| In the middle of Fig.1 an in-plane vibrational [[normal mode]] ''Q'' of the planar molecule is indicated by red arrows. Explicitly, the red arrows represent the mode
| | \lambda\begin{pmatrix}0\\ f\end{pmatrix} + (1-\lambda)\begin{pmatrix}x_1\\ -f\end{pmatrix}, \quad 0\le\lambda\le 1. |
| | </math> |
| | The midpoint ''A'' of ''FQ'' has coordinates (λ = ½): |
| | :<math> |
| | \frac{1}{2}\begin{pmatrix}0\\ f\end{pmatrix} + \frac{1}{2}\begin{pmatrix}x_1\\ -f\end{pmatrix} = |
| | \begin{pmatrix}\frac{1}{2} x_1\\ 0\end{pmatrix}. |
| | </math> |
| | Hence ''A'' lies on the ''x''-axis. |
| | The parabola has equation, |
| | :<math> |
| | y = \frac{1}{4f} x^2. |
| | </math> |
| | The equation of the tangent at ''P'' is |
| :<math> | | :<math> |
| Q = -\Delta x_1 - \Delta x_3 + \Delta y_2 + \Delta y_4,\,
| | y = y_1 + \frac{x_1}{2f} (x-x_1)\quad \hbox{with}\quad y_1 = \frac{x_1^2}{4f}. |
| </math> | | </math> |
| where the deviations of the atoms are all of the same length ''|q|''.<ref>For the record: ''Q'' transforms as ''B''<sub>''1g''</sub> of D<sub>4h</sub> and is a ''ν''<sub>2</sub> mode.</ref> When ''q'' is positive, the molecule is elongated along the ''y''-axis; this is the leftmost molecule in Fig. 1. Similarly, negative ''q'' implies a compression along the ''y''-axis and an elongation along the ''x''-axis (the rightmost molecule). The case ''q'' = 0 corresponds to the perfect square.
| | This line intersects the ''x''-axis at ''y'' = 0, |
| | |
| Both distorted molecules are of D<sub>2h</sub> symmetry; D<sub>2h</sub> is an [[Abelian group]] that has—as any Abelian group—only one-dimensional irreducible representations. Hence all electronic states of the distorted molecules are non-degenerate. The function |''X'' ⟩ transforms as ''B<sub>3u</sub>'' and |''Y'' ⟩ transforms as ''B<sub>2u</sub>'' of D<sub>2h</sub>. Let the respective energies be written as <math>\varepsilon_{X}</math> and <math>\varepsilon_{Y}</math>. Group theory tells us that these energies are different, but without explicit calculation it is not a priori clear which of the two energies is higher. Let us assume that for positive ''q'' : <math>\varepsilon_{X} < \varepsilon_{Y}</math>. This is shown in the energy level scheme in the bottom part of Fig. 1. An important observation now is that the leftmost and rightmost distorted molecules are essentially the same, they follow from each other by rotation over ±90° around the ''z''-axis (a rotation of the molecules in the ''xy''-plane). The ''x'' and ''y'' direction are interchanged between the left- and rightmost molecules by this rotation. Hence the molecule distorted with negative ''q''-value has the energies satisfying: <math>\varepsilon_{X} > \varepsilon_{Y}</math>. Summarizing,
| |
| :<math> | | :<math> |
| \varepsilon_X(q) = \varepsilon_Y(-q)\quad \hbox{and}\quad \varepsilon_X(-q) = \varepsilon_Y(q)\quad \hbox{with}\quad \varepsilon_X(q) <\varepsilon_Y(q)\quad\hbox{for}\quad q > 0.
| | 0 = \frac{x_1^2}{4f} - \frac{x_1^2}{2f} + \frac{x_1}{2f} x |
| | \Longrightarrow \frac{x_1}{2f} x = \frac{x_1^2}{4f} \longrightarrow x = \tfrac{1}{2}x_1. |
| </math> | | </math> |
| For small ''q''-values it is reasonable to assume that both <math>\varepsilon_{X}(q)</math> and <math>\varepsilon_{Y}(q)</math> are quadratic functions of ''q''. The parabolic energy curves are shown in Fig. 2. For ''q'' = 0 the energy curves cross and <math>\varepsilon_{X}(0) = \varepsilon_{Y}(0) \equiv \varepsilon_{E_u}</math>. The crossing point, corresponding to the perfect square, is clearly not an absolute minimum; therefore, the totally square symmetric configuration of the molecule will not be a stable equilibrium for the degenerate electronic state. At equilibrium, the molecule will be distorted along a normal mode away from square, and its energy will be lowered. This is the Jahn-Teller effect.
| | The intersection of the tangent with the ''x''-axis is the point ''A'' = (½''x''<sub>1</sub>, 0) that lies on the midpoint of ''FQ''. The corresponding sides of the triangles ''FPA'' and ''QPA'' are of equal length and hence the triangles are congruent. |
| | |
| The above arguments are not restricted to square molecules. With the exception of linear molecules, which show [[Renner-Teller effect]]s, all polyatomic molecules of sufficiently high symmetry to possess spatially degenerate electronic states will be subject to the Jahn-Teller instability. The proof, as given by Jahn and Teller, proceeds by application of point group symmetry | |
| principles; it rests on inspection of all molecular symmetry groups
| |
| | |
| ==Reference==
| |
| <references />
| |
| * R. Englman, ''The Jahn-Teller Effect in Molecules and Crystals'', Wiley, London (1972). ISBN-10: 0471241687 ISBN-13: 78-0471241683
| |
| * Isaac B. Bersuker, ''The Jahn-Teller Effect'', Cambridge University Press (2006). ISBN-10: 0521822122 ISBN-13: 9780521822121
| |
Parabolic mirror
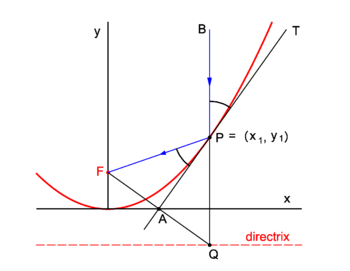
PD Image Fig. 2. Reflection in a parabolic mirror
Parabolic mirrors concentrate incoming vertical light beams in their focus. We show this.
Consider in figure 2 the arbitrary vertical light beam (blue, parallel to the y-axis) that enters the parabola and hits it at point P = (x1, y1). The parabola (red) has focus in point F. The incoming beam is reflected at P obeying the well-known law: incidence angle is angle of reflection. The angles involved are with the line APT which is tangent to the parabola at point P. It will be shown that the reflected beam passes through F.
Clearly ∠BPT = ∠QPA (they are vertically opposite angles). Further ∠APQ = ∠FPA because the triangles FPA and QPA are congruent and hence ∠FPA = ∠BPT.
We prove the congruence of the triangles: By the definition of the parabola the line segments FP and QP are of equal length, because the length of the latter segment is the distance of P to the directrix and the length of FP is the distance of P to the focus. The point F has the coordinates (0,f) and the point Q has the coordinates (x1, −f). The line segment FQ has the equation

The midpoint A of FQ has coordinates (λ = ½):

Hence A lies on the x-axis.
The parabola has equation,

The equation of the tangent at P is

This line intersects the x-axis at y = 0,

The intersection of the tangent with the x-axis is the point A = (½x1, 0) that lies on the midpoint of FQ. The corresponding sides of the triangles FPA and QPA are of equal length and hence the triangles are congruent.





