imported>Paul Wormer |
imported>Paul Wormer |
| (31 intermediate revisions by the same user not shown) |
| Line 1: |
Line 1: |
| In [[molecular physics]], the '''Jahn-Teller effect''' is the distortion of a highly symmetric—but non-linear—[[molecule]] to lower symmetry and lower energy. The effect occurs if the high-symmetric molecule would be in a degenerate state of definite energy, that is, if more than one [[wave function]] of the same energy would be [[eigenfunction]] of the [[molecular Hamiltonian]]. When energy degeneracy of a molecular state would arise—i.e., two or more orthogonal wave functions would describe the same molecular-energy eigenstate—it appears that a distorted, lower-symmetry, molecule will have lower, and accordingly more favorable, energy. Hence, by Jahn-Teller distortion, the molecule is lowered in symmetry and the energy degeneracy is lifted. Wave functions that would belong to the same energy in the high-symmetric molecule obtain different energies, some energies are lower, some higher.
| | ==Parabolic mirror== |
| | {{Image|Refl parab.png|right|350px|Fig. 2. Reflection in a parabolic mirror}} |
| | Parabolic mirrors concentrate incoming vertical light beams in their focus. We show this. |
|
| |
|
| The effect is named after [[Hermann Arthur Jahn|H. A. Jahn]] and [[Edward Teller|E. Teller]] who predicted it in 1937.<ref>H. A. Jahn and E. Teller, ''Stability of Polyatomic Molecules in Degenerate Electronic States'', Proc. Royal Soc. vol. '''161''', pp. 220–235 (1937)</ref> It took some time before the effect was experimentally observed, because it was masked by other molecular interactions. However, there are now numerous unambiguous observations that agree well with theoretical predictions. These range from the excited states of the simplest non-linear molecule H<sub>3</sub>, through moderate sized organic molecules, like [[cation]]s of substituted [[benzene]], to [[transition metal]] complexes and localized impurity centers in solids.
| | Consider in figure 2 the arbitrary vertical light beam (blue, parallel to the ''y''-axis) that enters the parabola and hits it at point ''P'' = (''x''<sub>1</sub>, ''y''<sub>1</sub>). The parabola (red) has focus in point ''F''. The incoming beam is reflected at ''P'' obeying the well-known law: incidence angle is angle of reflection. The angles involved are with the line ''APT'' which is tangent to the parabola at point ''P''. It will be shown that the reflected beam passes through ''F''. |
|
| |
|
| <font style = "font-size: 85%; font-style: oblique; font-weight: bold;" >
| | Clearly ∠''BPT'' = ∠''QPA'' (they are vertically opposite angles). Further ∠''APQ'' = ∠''FPA'' because the triangles ''FPA'' and ''QPA'' are congruent and hence ∠''FPA'' = ∠''BPT''. |
| :The Jahn-Teller effect has a quantum mechanical origin and there is no classical-physics explanation of it. Therefore, some knowledge of quantum mechanics is prerequisite to the reading of this article. Further [[Schönflies]] notation for [[point group]]s and [[Mulliken]] notation for their irreducible representations is used without further explanation. </font>
| |
| ==Explanation==
| |
| {{Image|Jahn-Teller.png|right|400px|Fig. 1 <small> The middle molecule at the top is square planar (point group D<sub>4h</sub>). The red arrows indicate a stretch-type normal mode and the rhombus-shaped molecules on either side are obtained by deforming the middle molecule along the normal mode. The degenerate electronic energy <math>\scriptstyle \mathcal{E}_\mathrm{E}</math> is split by the deformation as shown at the bottom.</small>}}
| |
| The Jahn-Teller effect is best explained by an example. Consider to that end the square homonuclear molecule in the middle of the top row of Fig. 1. The plane of the figure is the ''xy''-plane, with the ''y''-axis vertical and the ''x''-axis horizontal. The ''z''-axis points towards the reader.
| |
| The symmetry group of the middle molecule is D<sub>4h</sub>. Let there be two—in principle exact—electronic wave functions that together span the irreducible representation E<sub>''u''</sub> of this group. One wave function transforms as an ''x''-coordinate under D<sub>4h</sub> and is denoted by |X ⟩. Its partner transforms as a ''y''-coordinate and is denoted by |Y ⟩. In the case of the perfect square both wave functions have the same energy denoted by <math>\mathcal{E}_\mathrm{E}</math>.
| |
|
| |
|
| It may be helpful to mention that approximations for the wave functions can be obtained from two degenerate [[molecular orbital]]s |''x'' ⟩ and |''y'' ⟩ (together carrying E<sub>''u''</sub>) that are outside a closed-shell and share a single unpaired electron. A closed-shell wave function (a many-electron wave function consisting of doubly occupied molecular orbitals) is invariant under the group operations. The exact wave function |X ⟩ is then approximated by the closed-shell wave function times orbital |''x'' ⟩ containing the single electron, while |Y ⟩ is approximated by the closed-shell wave function times molecular orbital |''y''⟩ containing the electron. The orbital |''x'' ⟩ transforming as an ''x''-coordinate has the ''yz''-plane—a mirror plane—as a nodal plane, that is, the orbital vanishes in this plane and has plus sign to the right and minus sign to the left of the ''yz''-plane. Similarly the orbital |''y'' ⟩ has the ''xz''-plane as a nodal plane.
| | We prove the congruence of the triangles: By the definition of the parabola the line segments ''FP'' and ''QP'' are of equal length, because the length of the latter segment is the distance of ''P'' to the directrix and the length of ''FP'' is the distance of ''P'' to the focus. The point ''F'' has the coordinates (0,''f'') and the point ''Q'' has the coordinates (''x''<sub>1</sub>, −''f''). The line segment ''FQ'' has the equation |
| | |
| In the middle molecule shown in Fig. 1 an in-plane vibrational stretching [[normal mode]] ''Q'' of the planar molecule is indicated by red arrows. Explicitly, with respect to local, parallel, right-handed systems of axes, the red arrows represent the mode
| |
| :<math>
| |
| Q = -\Delta x_1 + \Delta x_3 + \Delta y_2 - \Delta y_4,\,
| |
| </math>
| |
| where the deviations of the atoms are all of the same length ''|q|''.<ref>For the record: ''Q'' transforms as B<sub>''1g''</sub> of D<sub>4h</sub> and is a ''ν''<sub>2</sub> mode.</ref> When ''q'' is positive, the molecule is elongated along the ''y''-axis and compressed along the ''x''-axis; this is the rightmost molecule in Fig. 1. Similarly, negative ''q'' implies a compression along the ''y''-axis and an elongation along the ''x''-axis (the leftmost molecule). The case ''q'' = 0 corresponds to the perfect square.
| |
| | |
| Both distorted [[rhombus]]-shaped molecules are of D<sub>2h</sub> symmetry; D<sub>2h</sub> is an [[Abelian group]] that has—as any Abelian group—only one-dimensional irreducible representations. Hence all electronic states of the distorted molecules are non-degenerate. The function |X ⟩ transforms as B<sub>3''u''</sub> and |Y ⟩ transforms as B<sub>2''u''</sub> of D<sub>2h</sub>. Let the respective energies be written as <math>\mathcal{E}_\mathrm{X}</math> and <math>\mathcal{E}_\mathrm{Y}</math>. Group theory tells us that these energies are different, but without explicit calculation it is not a priori clear which of the two energies is higher. Let us assume that for positive ''q'' : <math>\mathcal{E}_\mathrm{X} < \mathcal{E}_\mathrm{Y}</math>. This is shown in the energy level scheme in the bottom part of Fig. 1. An important observation now is that the leftmost and rightmost distorted molecules are essentially the same, they follow from each other by an in-plane rotation over ±90° around the ''z''-axis. The ''x'' and ''y'' direction are interchanged between the left- and rightmost molecules by this rotation. Hence the molecule distorted with negative ''q''-value has the energies satisfying: <math>\mathcal{E}_\mathrm{X} > \mathcal{E}_\mathrm{Y}</math>.
| |
| {{Image|J-T pot.png|left|300px|Fig. 2. Energies of state <nowiki>|X ⟩</nowiki> and state <nowiki>|Y ⟩</nowiki> as function of nuclear displacement ''q''. The case ''q'' <nowiki> = </nowiki>0 corresponds to the highly symmetric middle molecule of Fig. 1. }}
| |
| | |
| Summarizing,
| |
| :<math>
| |
| \mathcal{E}_\mathrm{X}(q) = \mathcal{E}_\mathrm{Y}(-q)
| |
| \quad
| |
| \hbox{and}
| |
| \quad
| |
| \mathcal{E}_\mathrm{X}(-q) = \mathcal{E}_\mathrm{Y}(q)
| |
| </math>
| |
| with
| |
| :<math>
| |
| \mathcal{E}_\mathrm{X}(q) <\mathcal{E}_\mathrm{Y}(q)\quad\hbox{for}\quad q > 0.
| |
| </math>
| |
| | |
| For small ''q''-values it is reasonable to assume that both <math>\mathcal{E}_\mathrm{X}(q)</math> and <math>\mathcal{E}_\mathrm{Y}(q)</math> are quadratic functions of ''q''. The quadratic energy curves are shown in Fig. 2. For ''q'' = 0 the energy curves cross and <math>\mathcal{E}_\mathrm{X}(0) = \mathcal{E}_\mathrm{Y}(0) \equiv \mathcal{E}_\mathrm{E}</math>. The crossing point, corresponding to the perfect square, is clearly not an absolute minimum; therefore, the totally square symmetric configuration of the molecule will not be a stable equilibrium for the degenerate electronic state. At equilibrium, the molecule will be distorted along a normal mode away from square, and its energy will be lowered. This is the Jahn-Teller effect.
| |
| | |
| The above arguments are not restricted to square molecules. With the exception of linear molecules, which show [[Renner-Teller effect]]s, all polyatomic molecules of sufficiently high symmetry to possess spatially degenerate electronic states will be subject to the Jahn-Teller instability. The proof, as given by Jahn and Teller and reproduced in the next section, proceeds by application of point group symmetry principles; it rests on inspection of all molecular symmetry groups
| |
| <br><br>
| |
| | |
| ==Jahn-Teller proof==
| |
| The proof given by Jahn and Teller in 1937 is based on first-order [[perturbation theory]] and application of [[point group]] symmetry.
| |
| | |
| Let us write '''r''' for the electronic coordinates and '''R''' for the nuclear coordinates of a molecule. The highly symmetric configuration (the one that is deformed by the Jahn-Teller effect) is designated by '''R'''<sub>0</sub>. The clamped nuclei Hamiltonian that arises in the first step of the [[Born-Oppenheimer approximation]] is
| |
| :<math>
| |
| H(\mathbf{r}, \mathbf{R}_0+\Delta\mathbf{R}) \approx H(\mathbf{r}, \mathbf{R}_0)
| |
| + \left( \frac{\partial H(\mathbf{r}, \mathbf{R})}{\partial \mathbf{R}}\right)_{\mathbf{R}_0}\Delta\mathbf{R},
| |
| </math>
| |
| where Δ'''R''' is a small deformation of the nuclear framework away from the symmetric case. The displacements are assumed to be infinitesimally small, i.e., |Δ'''R'''|<sup>2</sup> << |Δ'''R'''|. This means that the expansion of ''H'' can be truncated after the second term, but also that a first-order perturbation approximation is valid; higher-order approximations contain terms non-linear in the displacements.
| |
|
| |
| The first term on the right-hand side in the previous expression is the zeroth-order Hamiltonian, which by assumption has a degenerate set of electronic eigenstates spanning an irreducible representation μ of the point group of the (undeformed) molecule:
| |
| :<math>
| |
| H(\mathbf{r}, \mathbf{R}_0)\; \Phi^{(\mu)}_i(\mathbf{r}) = \mathcal{E}^{(0)}\; \Phi^{(\mu)}_i(\mathbf{r}), \quad i=1,\ldots,f_\mu,
| |
| </math>
| |
| where ''f''<sub>μ</sub> is the dimension of μ (the degree of degeneracy of <font style = "vertical-align: top;"><math>\mathcal{E}^{(0)}</math></font>). The second term is the perturbation
| |
| :<math> | | :<math> |
| V(\mathbf{r},\Delta\mathbf{R}) \equiv \left( \frac{\partial H(\mathbf{r}, \mathbf{R})}{\partial \mathbf{R}}\right)_{\mathbf{R}_0}\Delta\mathbf{R}.
| | \lambda\begin{pmatrix}0\\ f\end{pmatrix} + (1-\lambda)\begin{pmatrix}x_1\\ -f\end{pmatrix}, \quad 0\le\lambda\le 1. |
| </math> | | </math> |
| | | The midpoint ''A'' of ''FQ'' has coordinates (λ = ½): |
| In accordance with first-order perturbation theory the electronic energies of the slightly deformed molecule are given by
| |
| :<math> | | :<math> |
| \mathcal{E}^{(0)} + \mathcal{E}^{(1)}_i,\quad i=1,\ldots,f_\mu, | | \frac{1}{2}\begin{pmatrix}0\\ f\end{pmatrix} + \frac{1}{2}\begin{pmatrix}x_1\\ -f\end{pmatrix} = |
| | \begin{pmatrix}\frac{1}{2} x_1\\ 0\end{pmatrix}. |
| </math> | | </math> |
| where the first-order energies are the eigenvalues of the ''f''<sub>μ</sub>×''f''<sub>μ</sub> matrix with general element
| | Hence ''A'' lies on the ''x''-axis. |
| | The parabola has equation, |
| :<math> | | :<math> |
| \langle \Phi^{(\mu)}_i |V| \Phi^{(\mu)}_j \rangle, | | y = \frac{1}{4f} x^2. |
| </math> | | </math> |
| and the angular brackets imply integration over the electronic coordinates '''r'''.
| | The equation of the tangent at ''P'' is |
| | |
| In order to predict whether these matrix elements are vanishing, Jahn and Teller transformed the nuclear Cartesian displacement coordinates Δ''R''<sub>Aα</sub> to symmetry adapted coordinates ''Q''<sub>''k''</sub> by a linear non-singular transformation '''L'''
| |
| :<math> | | :<math> |
| Q_k = \sum_{A=1}^{N_\mathrm{nuc}}\sum_{\alpha =x,y,z} L_{k;A\alpha} \Delta R_{A\alpha},\quad k=1,\ldots,3N_\mathrm{nuc},
| | y = y_1 + \frac{x_1}{2f} (x-x_1)\quad \hbox{with}\quad y_1 = \frac{x_1^2}{4f}. |
| </math> | | </math> |
| where ''A'' runs over the ''N''<sub>nuc</sub> nuclei of the molecule and α over the Cartesian coordinates of '''R'''<sub>''A''</sub>. The elements of the matrix '''L''' can be determined by group theoretical projection (an example of a symmetry coordinate ''Q'' was given in the previous section; the example specifies one of the twelve rows of '''L'''). Jahn and Teller tabulate the irreducible representations carried by the nuclear coordinates for all possible point groups. They consider also the overall rotation and translation of the molecules.
| | This line intersects the ''x''-axis at ''y'' = 0, |
| | |
| For instance, they list that for the group D<sub>4h</sub> (the group of four nuclei on the corners of a square) the components of the translation vector span A<sub>2''u''</sub> and E<sub>1''u''</sub>. The rotation generators (components of the [[rigid rotor]] angular momentum) span A<sub>2''g''</sub> and E<sub>1''g''</sub>, and the internal (vibrational) coordinates span A<sub>1''g''</sub>, B<sub>1''g''</sub>, B<sub>2''g''</sub>, B<sub>2''u''</sub>, and E<sub>''u''</sub>. The twelve rows of the matrix '''L''' are labeled by these irreducible representations (and in the case of a more-dimensional representation μ by a further subindex running from 1 to to ''f''<sub>μ</sub>).
| |
| | |
| By a simple application of the chain rule it follows that
| |
| :<math> | | :<math> |
| V = \left( \frac{\partial H(\mathbf{r}, \mathbf{R})}{\partial \mathbf{R}}\right)_{\mathbf{R}_0}\Delta\mathbf{R} = \sum_{k=1}^{3N_\mathrm{nuc}-6}
| | 0 = \frac{x_1^2}{4f} - \frac{x_1^2}{2f} + \frac{x_1}{2f} x |
| \left( \frac{\partial H(\mathbf{r}, \mathbf{R}_0+\mathbf{Q})} {\partial Q_k}\right)_{\mathbf{Q}=\mathbf{0}} Q_k \equiv \sum_{k=1}^{3N_\mathrm{nuc}-6} V_k(\mathbf{r}) Q_k,
| | \Longrightarrow \frac{x_1}{2f} x = \frac{x_1^2}{4f} \longrightarrow x = \tfrac{1}{2}x_1. |
| </math> | | </math> |
| where it is assumed that the molecule moves in a homogeneous and isotropic space so that ''V'' does not depend on the 3 translational and 3 rotational symmetry coordinates. For the groups of interest ∂/∂''Q''<sub>''k''</sub> transforms as ''Q''<sub>''k''</sub> and hence ''V''<sub>''k''</sub>('''r''') is an operator that transforms according to the same irreducible representation as ''Q''<sub>''k''</sub>. It is a multiplicative operator, i.e.,
| | The intersection of the tangent with the ''x''-axis is the point ''A'' = (½''x''<sub>1</sub>, 0) that lies on the midpoint of ''FQ''. The corresponding sides of the triangles ''FPA'' and ''QPA'' are of equal length and hence the triangles are congruent. |
| :<math>
| |
| \Phi^{(\mu)}_i(\mathbf{r}) V_k(\mathbf{r}) \Phi^{(\mu)}_j(\mathbf{r}) = \Phi^{(\mu)}_i(\mathbf{r})\Phi^{(\mu)}_j(\mathbf{r}) V_k(\mathbf{r}),
| |
| </math>
| |
| since the electronic kinetic energy terms are contained in the zeroth-order Hamiltonian ''H''('''r''', '''R'''<sub>0</sub>). The groups of interest all have real irreducible representation matrices, which implies that the zeroth-order wave functions are real.
| |
| | |
| The product <font style="vertical-align: text-top;"><math>\Phi^{\mu}_i\Phi^{\mu}_j</math></font> spans the symmetrized representation [μ<sup>2</sup>], which is of dimension ''f''<sub>μ</sub>(''f''<sub>μ</sub> + 1)/2 and reducible if ''f''<sub>μ </sub> > 1. Jahn and Teller tabulate the decompositions of all symmetrized representations of all pertinent groups in irreducible components. For instance for D<sub>4h</sub>:
| |
| :<math>
| |
| [\mathrm{E}^2_{g}] = [\mathrm{E}^2_{u}] = \mathrm{A}_{1g} \oplus \mathrm{B}_{1g} \oplus \mathrm{B}_{2g}.
| |
| </math>
| |
| | |
| Group theory tells us that a perturbation matrix element
| |
| :<math>
| |
| \langle \Phi^{(\mu)}_i| V_k | \Phi^{(\mu)}_j \rangle = 0
| |
| </math>
| |
| ''unless the irreducible representation of'' ''V''<sub>''k''</sub> ''is contained in the decomposition of'' [μ<sup>2</sup>]. By inspection of their tables Jahn and Teller found that all symmetry groups of all non-linear molecules have at least one (but usually more) non-vanishing perturbation matrix elements.
| |
| | |
| For instance, assume that a molecule with D<sub>4h</sub> symmetry has a zeroth-order electronic state belonging to E<sub>''u''</sub>. One needs to inspect
| |
| :<math>
| |
| (\mathrm{A}_{1g}\oplus\mathrm{B}_{1g}\oplus\mathrm{B}_{2u}\oplus\mathrm{E}_{u}) \otimes (\mathrm{A}_{1g}\oplus\mathrm{B}_{1g} \oplus \mathrm{B}_{2g}),
| |
| </math>
| |
| where the first factor corresponds to ''V'' and the second to [E<sub>''u''</sub><sup>2</sup>]. Non-vanishing cases are A<sub>1''g''</sub>⊗A<sub>1''g''</sub> and B<sub>1''g''</sub>⊗B<sub>1''g''</sub>
| |
| | |
| Say a matrix element of ''V''<sub>''k''</sub> ≠ 0. Then the corresponding displacement ''Q''<sub>''k''</sub> appears linearly in the lowest first-order energy correction (lowest eigenvalue of the perturbation matrix); terms of higher order in the infinitesimal coordinate ''Q''<sub>''k''</sub> can be ignored. Suppose this lowest first-order energy correction contains ''CQ''<sub>''k''</sub> with some real constant ''C''. If ''C'' > 0 then a displacement along −''Q''<sub>''k''</sub> lowers the electronic energy and the molecule will deform in that direction. If ''C'' < 0 then a displacement along ''Q''<sub>''k''</sub> decreases the electronic energy. The case ''C'' = 0 only arises when the whole perturbation matrix is zero and this case is excluded.
| |
| | |
| In the previous example for D<sub>4h</sub>, the case A<sub>1g</sub>⊗A<sub>1g</sub> corresponds to a symmetric stretch that does not lower the symmetry of the molecule. During this "breathing" vibration the molecule alternately expands and shrinks, but keeps its shape. The other non-zero case is B<sub>1g</sub>⊗B<sub>1g</sub>. This corresponds to a deformation of the molecule along a coordinate ''Q'' of B<sub>1g</sub> symmetry. This corresponds to a deformation of the square molecule to a rhombus-shaped molecule, as was shown in the previous section.
| |
| | |
| ==Reference==
| |
| <references />
| |
| * R. Englman, ''The Jahn-Teller Effect in Molecules and Crystals'', Wiley, London (1972). ISBN-10: 0471241687 ISBN-13: 78-0471241683
| |
| * Isaac B. Bersuker, ''The Jahn-Teller Effect'', Cambridge University Press (2006). ISBN-10: 0521822122 ISBN-13: 9780521822121
| |
Parabolic mirror
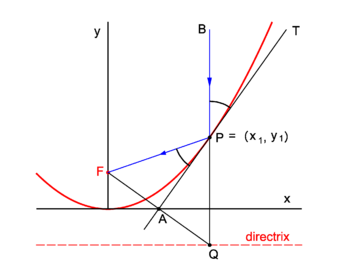
PD Image Fig. 2. Reflection in a parabolic mirror
Parabolic mirrors concentrate incoming vertical light beams in their focus. We show this.
Consider in figure 2 the arbitrary vertical light beam (blue, parallel to the y-axis) that enters the parabola and hits it at point P = (x1, y1). The parabola (red) has focus in point F. The incoming beam is reflected at P obeying the well-known law: incidence angle is angle of reflection. The angles involved are with the line APT which is tangent to the parabola at point P. It will be shown that the reflected beam passes through F.
Clearly ∠BPT = ∠QPA (they are vertically opposite angles). Further ∠APQ = ∠FPA because the triangles FPA and QPA are congruent and hence ∠FPA = ∠BPT.
We prove the congruence of the triangles: By the definition of the parabola the line segments FP and QP are of equal length, because the length of the latter segment is the distance of P to the directrix and the length of FP is the distance of P to the focus. The point F has the coordinates (0,f) and the point Q has the coordinates (x1, −f). The line segment FQ has the equation

The midpoint A of FQ has coordinates (λ = ½):

Hence A lies on the x-axis.
The parabola has equation,

The equation of the tangent at P is

This line intersects the x-axis at y = 0,

The intersection of the tangent with the x-axis is the point A = (½x1, 0) that lies on the midpoint of FQ. The corresponding sides of the triangles FPA and QPA are of equal length and hence the triangles are congruent.





