User talk:Paul Wormer/scratchbook1: Difference between revisions
imported>Paul Wormer No edit summary |
imported>Paul Wormer No edit summary |
||
| Line 10: | Line 10: | ||
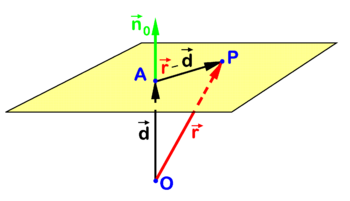
is a unit (length 1) vector normal (perpendicular) to the plane. Evidently ''a'' is the distance of ''O'' to the plane. The following relation holds for an arbitrary point ''X'' in the plane | is a unit (length 1) vector normal (perpendicular) to the plane. Evidently ''a'' is the distance of ''O'' to the plane. The following relation holds for an arbitrary point ''X'' in the plane | ||
:<math> | :<math> | ||
\left(\vec{\mathbf{r}}-\vec{\mathbf{a}}\right)\cdot \hat{\mathbf{n}} = 0 \quad\hbox{with}\quad \vec{\mathbf{r}} \equiv\overrightarrow{OX} . | \left(\vec{\mathbf{r}}-\vec{\mathbf{a}}\right)\cdot \hat{\mathbf{n}} = 0 \quad\hbox{with}\quad \vec{\mathbf{r}} \equiv\overrightarrow{OX}\quad\hbox{and}\quad \overrightarrow{AX} = \vec{\mathbf{r}}-\vec{\mathbf{a}} . | ||
</math> | </math> | ||
Revision as of 05:06, 30 March 2010
In analytic geometry several closely related algebraic equations are known for a plane in three-dimensional Euclidean space. One such equation is illustrated in the figure. Point X is an arbitrary point in the plane and O (the origin) is outside the plane. The point A in the plane is chosen such that vector
is orthogonal to the plane. The collinear vector
is a unit (length 1) vector normal (perpendicular) to the plane. Evidently a is the distance of O to the plane. The following relation holds for an arbitrary point X in the plane
This equation for the plane can be rewritten in terms of coordinates with respect to a Cartesian frame with origin in O. Dropping arrows and hat for component vectors (real triples), we find
with
Conversely, given the following equation for a plane
writing
it follows that
Hence
where f , a, and n are collinear.