User:John R. Brews/Fourier series: Difference between revisions
imported>John R. Brews |
No edit summary |
||
| (9 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
{{AccountNotLive}} | |||
==Fourier series (music)== | ==Fourier series (music)== | ||
{{Image|Sound envelope of a musical note.png|right|180px|The amplitude of a musical note varies in time according to its sound envelope.<ref name=Alten/>}} | {{Image|Sound envelope of a musical note.png|right|180px|The amplitude of a musical note varies in time according to its sound envelope.<ref name=Alten/>}} | ||
The ideas of [[Fourier series]] have interesting application in [[music]], for example, in illuminating the differences in [[ | The ideas of [[Fourier series]] have interesting application in [[music]], for example, in illuminating the differences in [[tone]] between [[musical instrument]]s and in the construction of [[music synthesizer]]s.<ref name=Gunther/> A laboratory determination of [[Pitch (music)|pitch]] is made by a subject listening to a note and to the tone of a single sinusoidal wave of a variable frequency, and identifying at what frequency the note and the sinusoid sound alike.<ref name=Rossing/> However, the tone of an instrument is determined only partially by pitch. | ||
The [[frequency spectrum]] of a musical instrument playing a particular note varies with the instrument and with the way that it is played. The manner of playing determines the [[Envelope function|sound envelope]] of a note, and therefore the amplitude of its harmonics.<ref name=Alten/> | |||
Some instruments (like the [[flute]] or the [[violin]]) exhibit a fundamental frequency and its harmonics in varying amplitudes and phase, and others (like the [[cymbal]] or the [[drum]]) do not.<ref name=Gunther/><ref name=Hopkin/> | Some instruments (like the [[flute]] or the [[violin]]) exhibit a fundamental frequency and its harmonics in varying amplitudes and phase, and others (like the [[cymbal]] or the [[drum]]) do not.<ref name=Gunther/><ref name=Hopkin/> | ||
| Line 10: | Line 13: | ||
|<font face="Gill Sans MT">It is well known that this union of several simple tones into one compound tone, which is naturally effected in the tones produced by most musical instruments, is artificially imitated on the organ by peculiar mechanical contrivances. The tones of organ-pipes are comparatively poor in upper partials. When it is desirable to use a stop of incisive penetrating quality of tone and great power, the wide pipes (''principal register'' and ''weithgedackt'') are not sufficient; their tone is too soft too defective in upper partials; and the narrow pipes (''geigen-register'' and ''quintaten'') are also unsuitable, because, although more incisive, their tone is weak. For such occasions, then, as in accompanying congregational singing, recourse is had to the ''compound stops''. In these stops every key is connected with a large or smaller series of pipes, which it opens simultaneously, and which give the prime tone and a certain number of the first upper partials of the compound tone of the note in question.</font> Helmholtz, p. 91<ref name=Helmholtz/> | |<font face="Gill Sans MT">It is well known that this union of several simple tones into one compound tone, which is naturally effected in the tones produced by most musical instruments, is artificially imitated on the organ by peculiar mechanical contrivances. The tones of organ-pipes are comparatively poor in upper partials. When it is desirable to use a stop of incisive penetrating quality of tone and great power, the wide pipes (''principal register'' and ''weithgedackt'') are not sufficient; their tone is too soft too defective in upper partials; and the narrow pipes (''geigen-register'' and ''quintaten'') are also unsuitable, because, although more incisive, their tone is weak. For such occasions, then, as in accompanying congregational singing, recourse is had to the ''compound stops''. In these stops every key is connected with a large or smaller series of pipes, which it opens simultaneously, and which give the prime tone and a certain number of the first upper partials of the compound tone of the note in question.</font> Helmholtz, p. 91<ref name=Helmholtz/> | ||
|} | |} | ||
These words identify the organ as a form of mechanical rather than | These words identify the organ as a form of mechanical rather than electronic music synthesizer. They also lay out the characterization of a musical note by its constituent frequency components, in the same way that a Fourier series expresses a periodic waveform in terms of its harmonic components. | ||
==Fourier series== | ==Fourier series== | ||
{{Main|Fourier series}} | {{Main|Fourier series}} | ||
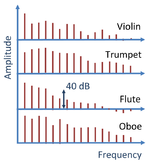
A musical note is a a periodic function in time and in space, modulated by a sound envelope. That is, the note can be expressed as: | {{Image|Instrument spectra (A4-440Hz).png|right|150px|Approximate spectrum of four instruments playing A4: 440 Hz}} | ||
As the remarks of Helmholtz suggest, the sound of a note played upon each instrument is characterized by not only its fundamental tone or frequency, which is the same for all instruments, but by the higher partial tones or harmonics in the note, which are different in amplitude and in phase for each instrument, making them sound different. | |||
A musical note is a a periodic function in time and in space, modulated by a sound envelope. That is, the note can be expressed in one spatial dimension as: | |||
:<math>n(x,\ t) = s(x-vt)f(x-vt) \ , </math> | :<math>n(x,\ t) = s(x-vt)f(x-vt) \ , </math> | ||
where ''s'' is the sound envelope that expresses the duration of the note at a fixed location or its extent in space at a fixed time, and ''f'' is a periodic function of its argument: | where ''s'' is the sound envelope that expresses the duration of the note at a fixed location or its extent in space at a fixed time, and ''f'' is a periodic function of its argument: | ||
:<math>f(x+\lambda -vt)=f\left(x-v(t+T)\right) = f(x-vt) \ , </math> | :<math>f(x+\lambda -vt)=f\left(x-v(t+T)\right) = f(x-vt) \ , </math> | ||
with ''λ'' the ''wavelength'' of ''f'' and ''T = λ/v'' the ''period'' of ''f'' and ''v'' the ''speed of propagation'' of ''f'' through space. | with ''λ'' the ''wavelength'' of ''f'' and ''T = λ/v'' the ''period'' of ''f'' and ''v'' the ''speed of propagation'' of ''f'' through space. | ||
The periodic factor in such a wave can be analyzed using a [[Fourier series]] to show it is made up of a summation of sinusoidal waves, each with their own frequency. These frequency components are useful in distinguishing the different characteristics of the same note played upon different instruments, as shown approximately in the figure. The spectrum is altered somewhat by the sound envelope, so the musician has some control over the tone. | |||
Naturally, besides the tone produced by the instrument, the musical experience also depends upon how the ear responds to the tone, and how the tone is modified by the auditorium where it propagates.<ref name= Howard/> | |||
where | |||
==References== | ==References== | ||
| Line 43: | Line 36: | ||
{{cite book |title=Audio in Media |author=Stanley R. Alten |url=http://books.google.com/books?id=ix4ok8ZQVFIC&pg=PA13 |chapter=Sound envelope |isbn= 049557239X |edition=12th ed |publisher=Cengage Learning |year=2010|pages=p. 13}} | {{cite book |title=Audio in Media |author=Stanley R. Alten |url=http://books.google.com/books?id=ix4ok8ZQVFIC&pg=PA13 |chapter=Sound envelope |isbn= 049557239X |edition=12th ed |publisher=Cengage Learning |year=2010|pages=p. 13}} | ||
</ref> | </ref> | ||
| Line 70: | Line 57: | ||
</ref> | </ref> | ||
<ref name=Howard> | |||
{{cite book |title=Acoustics and Psychoacoustics |author=David Martin Howard, Jamie Angus |chapter=§3.1.2 Musical notes and their harmonics |url=http://books.google.com/books?id=qgsst2OQYJEC&pg=PA124 |isbn=0240521757 |publisher=Focal Press |year=2009 |pages=pp. 124 ''ff'' |edition=4rth ed}} | |||
</ref> | |||
<ref name= | <ref name=Rossing> | ||
{{cite book |title= | {{cite book |title=Springer Handbook of Acoustics |author=Thomas D. Rossing |url=http://books.google.com/books?id=4ktVwGe_dSMC&pg=PA477 |pages=p. 477 |isbn=0387304460 |year=2007 |publisher=Springer}} | ||
| | |||
</ref> | </ref> | ||
}} | }} | ||
Latest revision as of 03:07, 22 November 2023
The account of this former contributor was not re-activated after the server upgrade of March 2022.
Fourier series (music)
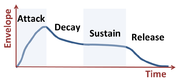
The amplitude of a musical note varies in time according to its sound envelope.[1]
The ideas of Fourier series have interesting application in music, for example, in illuminating the differences in tone between musical instruments and in the construction of music synthesizers.[2] A laboratory determination of pitch is made by a subject listening to a note and to the tone of a single sinusoidal wave of a variable frequency, and identifying at what frequency the note and the sinusoid sound alike.[3] However, the tone of an instrument is determined only partially by pitch.
The frequency spectrum of a musical instrument playing a particular note varies with the instrument and with the way that it is played. The manner of playing determines the sound envelope of a note, and therefore the amplitude of its harmonics.[1]
Some instruments (like the flute or the violin) exhibit a fundamental frequency and its harmonics in varying amplitudes and phase, and others (like the cymbal or the drum) do not.[2][4]
Helmholtz' theory
A single note is often referred to as a tone, the lowest frequency present as the fundamental or prime partial tone and harmonics of this frequency that appear when a note is played on an instrument as harmonic upper partial tones or upper tones or partial tones. Where only one frequency is present, as with a tuning fork, it is called a simple tone:[5]
| It is well known that this union of several simple tones into one compound tone, which is naturally effected in the tones produced by most musical instruments, is artificially imitated on the organ by peculiar mechanical contrivances. The tones of organ-pipes are comparatively poor in upper partials. When it is desirable to use a stop of incisive penetrating quality of tone and great power, the wide pipes (principal register and weithgedackt) are not sufficient; their tone is too soft too defective in upper partials; and the narrow pipes (geigen-register and quintaten) are also unsuitable, because, although more incisive, their tone is weak. For such occasions, then, as in accompanying congregational singing, recourse is had to the compound stops. In these stops every key is connected with a large or smaller series of pipes, which it opens simultaneously, and which give the prime tone and a certain number of the first upper partials of the compound tone of the note in question. Helmholtz, p. 91[5] |
These words identify the organ as a form of mechanical rather than electronic music synthesizer. They also lay out the characterization of a musical note by its constituent frequency components, in the same way that a Fourier series expresses a periodic waveform in terms of its harmonic components.
Fourier series
As the remarks of Helmholtz suggest, the sound of a note played upon each instrument is characterized by not only its fundamental tone or frequency, which is the same for all instruments, but by the higher partial tones or harmonics in the note, which are different in amplitude and in phase for each instrument, making them sound different.
A musical note is a a periodic function in time and in space, modulated by a sound envelope. That is, the note can be expressed in one spatial dimension as:
where s is the sound envelope that expresses the duration of the note at a fixed location or its extent in space at a fixed time, and f is a periodic function of its argument:
with λ the wavelength of f and T = λ/v the period of f and v the speed of propagation of f through space.
The periodic factor in such a wave can be analyzed using a Fourier series to show it is made up of a summation of sinusoidal waves, each with their own frequency. These frequency components are useful in distinguishing the different characteristics of the same note played upon different instruments, as shown approximately in the figure. The spectrum is altered somewhat by the sound envelope, so the musician has some control over the tone.
Naturally, besides the tone produced by the instrument, the musical experience also depends upon how the ear responds to the tone, and how the tone is modified by the auditorium where it propagates.[6]
References
- ↑ 1.0 1.1 Stanley R. Alten (2010). “Sound envelope”, Audio in Media, 12th ed. Cengage Learning, p. 13. ISBN 049557239X.
- ↑ 2.0 2.1 Leon Gunther (2011). The Physics of Music and Color. Springer, p. 47 ff. ISBN 1461405564.
- ↑ Thomas D. Rossing (2007). Springer Handbook of Acoustics. Springer, p. 477. ISBN 0387304460.
- ↑ Bart Hopkin (1996). “Figure 2-4”, Musical Instrument Design: Practical Information for Instrument Making. See Sharp Press, p. 110. ISBN 1884365086.
- ↑ 5.0 5.1 Hermann Ludwig F. von Helmholtz (1875). On the sensations of tone as a physiological basis for the theory of music, Translation by Alexander John Ellis. Oxford University Press, p. 33.
- ↑ David Martin Howard, Jamie Angus (2009). “§3.1.2 Musical notes and their harmonics”, Acoustics and Psychoacoustics, 4rth ed. Focal Press, pp. 124 ff. ISBN 0240521757.
- Thomas D. Rossing (2007). Springer Handbook of Acoustics. Springer, p. 541. ISBN 0387304460.