imported>Felipe Ortega Gutiérrez |
|
| (5 intermediate revisions by 3 users not shown) |
| Line 1: |
Line 1: |
| '''Artificial neurons''' are processing units based on the biological neural model. The first artificial neuron model was created by McCullough and Pitts, and then newer and more complex models have appeared. Since the connectivity in the biological neurons is higher, artificial neurons must be considered as only an approximation to the biological model.
| | {{subpages}} |
|
| |
|
| Artificial neurons can be organized and connected in order to create [[Artificial Neural Network|artificial neural networks]], which process the data carried through the neural connections in different layers. Learning algorithms can also be applied to artificial neural networks in order to modify their behavior. | | '''Artificial neurons''' are processing units based on a neural model, often inspired on the biological neurons. The first artificial neuron model was created by McCullough and Pitts, since when newer and more realistic models have appeared. |
|
| |
|
| [[Image:artificialneuron.png|thumb|450px|McCullough-Pitts neuron with 4 inputs.]] | | Artificial neurons can be associated in order to create [[Artificial Neural Network|artificial neural networks]], which process the data carried through the neural connections. |
| | |
| | [[Image:artificialneuron.png|thumb|450px|Artificial neuron with 4 inputs.]] |
|
| |
|
| ==Behavior== | | ==Behavior== |
| A neuron may have multiple inputs, each input has an assigned value called ''weight'', which represents the strength of the connection between the source and destination neuron. The input signal value is multiplied by the ''weight'' <math>w \in \left[0 \dots 1\right]</math>.
| | Neural processing involves the following operations: |
| | |
| | |
| The sum of all input values multiplied by their respective weights is called ''activation'', or ''weighted-sum''. It represents the sum of all the input values, considering the strength each input connection.
| |
| | |
| <center><math>a = \sum_{i=0}^n w_i x_i</math></center>Where <math>w_i</math> is the weight of the connection between the current neuron and the ith neuron, and <math>x_i</math> is the value coming from the ith neuron.
| |
| | |
| After the activation is produced, a function modifies it, producing an output. That function is often called ''transfer function'' and its purpose is to filter the activation. The output value <math>y</math> can be expressed as:
| |
| | |
| <center><math>y = \varphi \left( \sum_{i=0}^n w_i x_i \right)</math></center>
| |
| | |
| ==Transfer Functions==
| |
| '''Transfer function''' is the name given for the functions which filter the activation value. This functions can be discrete or continuous. Some of the most used transfer functions are:
| |
| | |
| ===Step function===
| |
| The step function (also called hard-limiter) is [[piecewise defined function]] used to produce [[binary]] outputs. In this function, the result is 0 if the activation is less than a value called ''threshold'', often symbolized with theta (<math>\theta</math>). Otherwise, the result is 1.
| |
| | |
| | |
| <center><math>y = \left\{ \begin{matrix} 1 & \mbox{if }a \ge \theta \\ 0 & \mbox{if }a < \theta \end{matrix} \right.</math></center>
| |
| | |
| ===Ramping function===
| |
| The ramping function is also a piecewise defined function, shaped as a ramp. It's mathematically defined as follows:
| |
| | |
| | |
| <center><math>y = \left\{ \begin{matrix} 0 & \mbox{if }a<0 \\ a & \mbox{if } a \ge 0 \\ 1 & \mbox{if }a \ge 1 \end{matrix}\right.</math></center>
| |
| | |
| ===Sigmoid===
| |
| The sigmoid function is used to produce continuous values. It's an S-shaped curve, and it's used when the inputs are between 0 and 1.
| |
| | |
| <center><math>\sigma \left( a \right) = \frac{1}{1+\exp\bigg(\frac{-a-\theta}{\rho}\bigg)}</math></center>
| |
| | |
| | |
| Where <math>a</math> is the activation, <math>\theta</math> is the ''threshold'' (that can be zero, simplifying the equation), and <math>\rho</math> is a value which defines the curvature of the sigmoid.
| |
| | |
| ===Hyperbolic Tangent===
| |
| The hyperbolic tangent is an [[hyperbolic trigonometric function]], used when the activation values are between -1 and 1. Its shape is very similar to the shape of the sigmoid.
| |
| | |
| <center><math>y = \tanh \left( a \right)</math></center>
| |
| | |
| | |
| ===Other functions===
| |
| There are even more functions used as transfer functions, such as: sine, cosine, linear combination, and others.
| |
| | |
| ==Pattern classification==
| |
| The space in which the inputs belong is the pattern space. The number of dimensions of the pattern space is defined by the number of inputs of the neuron. For this reason, when the number of inputs is greater than three, the pattern space is called '''pattern hyperspace'''.
| |
|
| |
|
| The pattern hyperspace can be separated by decision hypersurfaces, which performs '''classification''' (separation of different portions of the pattern hyperspace into "classes").
| | a) Synaptic operation. Processes incoming data, considering the strength of each connection (often represented as a value called ''weight''). |
|
| |
|
| ==Analogy to Biological Neurons==
| | b) Somatic operation. Provides operations such as thresholding, aggregation, non-linear activation and dynamic processing to the synaptic inputs. Most of these operations are used to implement a threshold effect. |
| In biological neurons there is a similar behavior. Inputs are electrical pulses transmitted to the [[synapses]] (terminals in the dendrites). Electrical pulses produce a release of [[neurotransmitter|neurotransmitters]] which may alter the dendritic membrane potential (''Post Synaptic Potential''). The Post Synaptic Potential travels over the axon, reaching another neuron, which will sum all the Post Synaptic Potentials received, and fire an output if the total sum of the Post Synaptic Potentials in the axon hillock received exceeds a threshold.
| |
|
| |
|
| [[Category:CZ Live]] | | ==Analogy to biological neurons== |
| [[Category:Computers Workgroup]] | | In biological neurons there is a similar behavior. Inputs are electrical pulses transmitted to the [[synapses]] (terminals in the dendrites). Electrical pulses produce a release of [[neurotransmitter|neurotransmitters]] which may alter the dendritic membrane potential (''post-synaptic potential''). The post-synaptic potential travels over the axon, reaching another neuron, which will sum all the post-synaptic potentials received, and fire an output if the total sum of the post-synaptic potentials in the axon hillock received exceeds a threshold.[[Category:Suggestion Bot Tag]] |
Artificial neurons are processing units based on a neural model, often inspired on the biological neurons. The first artificial neuron model was created by McCullough and Pitts, since when newer and more realistic models have appeared.
Artificial neurons can be associated in order to create artificial neural networks, which process the data carried through the neural connections.
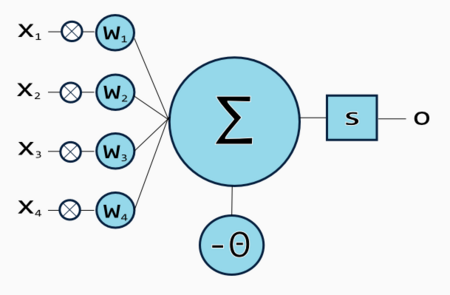
Artificial neuron with 4 inputs.
Behavior
Neural processing involves the following operations:
a) Synaptic operation. Processes incoming data, considering the strength of each connection (often represented as a value called weight).
b) Somatic operation. Provides operations such as thresholding, aggregation, non-linear activation and dynamic processing to the synaptic inputs. Most of these operations are used to implement a threshold effect.
Analogy to biological neurons
In biological neurons there is a similar behavior. Inputs are electrical pulses transmitted to the synapses (terminals in the dendrites). Electrical pulses produce a release of neurotransmitters which may alter the dendritic membrane potential (post-synaptic potential). The post-synaptic potential travels over the axon, reaching another neuron, which will sum all the post-synaptic potentials received, and fire an output if the total sum of the post-synaptic potentials in the axon hillock received exceeds a threshold.
