Gamma function: Difference between revisions
imported>Fredrik Johansson |
mNo edit summary |
||
| (114 intermediate revisions by 10 users not shown) | |||
| Line 1: | Line 1: | ||
{{subpages}} | |||
The '''gamma function''' is a mathematical function that extends the domain of [[factorial]]s to non-integers. The factorial of a positive integer ''n'', written ''n''!, is the product 1·2·3···''n''. The gamma function, denoted by <math>\Gamma</math>, is defined to satisfy <math>\Gamma(n) = (n-1)!</math> for all positive integers ''n'' and to smoothly interpolate the factorial between the integers. The gamma function is one of the most commonly occurring examples of a nonelementary function; that is, a function that cannot be expressed in finite terms using algebraic operations, exponentials, and logarithms. Its study dates back to [[Leonhard Euler]], who gave a formula for its calculation in 1729. | The '''gamma function''' is a mathematical function that extends the domain of [[factorial]]s to non-integers. The factorial of a positive integer ''n'', written ''n''!, is the product 1·2·3···''n''. The gamma function, denoted by <math>\Gamma</math>, is defined to satisfy <math>\Gamma(n) = (n-1)!</math> for all positive integers ''n'' and to smoothly interpolate the factorial between the integers. The gamma function is one of the most commonly occurring examples of a nonelementary function; that is, a function that cannot be expressed in finite terms using algebraic operations, exponentials, and logarithms. Its study dates back to [[Leonhard Euler]], who gave a formula for its calculation in 1729. | ||
| Line 5: | Line 7: | ||
[[Image:Factorial interpolation.png|thumb|250px|It is easy to graphically interpolate the factorial to non-integer values, but is there a formula that describes the resulting curve?]] | [[Image:Factorial interpolation.png|thumb|250px|It is easy to graphically interpolate the factorial to non-integer values, but is there a formula that describes the resulting curve?]] | ||
The gamma function can be seen as a solution to the following [[interpolation]] problem: find a smooth curve that connects the points given by <math>\scriptstyle y = 1 \cdot 2 \cdots x = x!</math> at the positive integers. A plot of the first few factorials makes clear that such a curve can be drawn (for example by hand), but it would be preferable to have a formula that precisely describes the curve. The formula for the factorial <math>n!</math> cannot be used directly for fractional values of <math>n</math> since the number of factors depends on <math>n</math> and only is valid when <math>n</math> is an integer. The solution would have to be a [[closed-form expression]], in which the number of operations does not depend on the size of <math>n</math>. | |||
There is a quite analogous problem for which the solution is simple. A famous anecdote goes that [[Carl Friedrich Gauss]], as a child, found that the sum <math>1+2+...+n</math> can be calculated as <math>n(n+1)/2</math> and that he thereby was able to quickly sum all the integers between 1 and 100, to the astonishment of his teacher. The formula <math>y = x(x+1)/2</math> is of course valid for fractional values of <math>x</math> and describes the simple shape known as a [[parabola]]. | |||
The analogy is that simply changing the "+" sign in <math>1+2+...+n</math> to a "<math>\cdot</math>" gives the factorial interpolation problem; however, Gauss's closed-form solution to the one problem cannot be translated to the other. There is in fact no such simple solution for factorials. Any combination of sums, products, powers, [[exponential function]]s or [[logarithm]]s with a fixed number of terms will not suffice to express <math>n!</math>: with more precise terminology, the factorial is not an [[elementary function]]. But it is possible to find a general formula for factorials with some more work, by deploying tools such as [[integral]]s and [[limit (mathematics)|limit]]s from [[calculus]]. It is this non-elementary solution that is called the gamma function. | |||
It must be noted that there are actually infinitely many extensions of the factorial to non-integers (each of them non-elementary): infinitely many curves can be drawn through any set of isolated points. The gamma function is distinguished by uncontestedly being the most useful solution in practice. The question of the gamma function's uniqueness will be discussed in more detail later on; we will first give the exact definition of the gamma function and state its fundamental properties. | |||
==Basic properties of the gamma function== | |||
===Euler's integral definition=== | |||
The gamma function is commonly defined by a [[definite integral]] due to [[Leonhard Euler]], | |||
to | |||
:<math>\Gamma(z | :<math>\Gamma(z)=\int_{0}^{\infty}e^{-t}t^{z-1}dt,</math> | ||
where <math>t^{z-1}</math> is interpreted as <math>e^{(z-1) \log t}</math> if <math>z</math> is not an integer.<ref>Everywhere in this article, "log" denotes the [[natural logarithm]].</ref> Using standard theorems from [[mathematical analysis]], it can be shown that Euler's integral defines <math>\Gamma</math> to be a [[continuous function]] if <math>z</math> is positive. In fact, Euler's integral is valid for any [[complex number]] <math>z</math> with a positive real part and defines the gamma function to be an [[analytic function]] in the positive complex half-plane.<ref>In the remainder of this article, "positive" will be understood to mean either a positive real number or a complex number with positive real part.</ref> | |||
To see that the gamma function corresponds to the factorial at integers, we can insert <math>z+1</math> instead of <math>z</math> and perform an [[integration by parts]] to obtain | |||
:<math>\Gamma(z+1)=\left[-e^{-t}t^{z}\right]_{0}^{\infty}+z\int_{0}^{\infty}e^{-t}t^{z-1}dt=z\Gamma(z).</math> | |||
This relation is called the ''recurrence formula'' or ''recurrence relation'' of the gamma function. The equation <math>f(z+1) = z f(z)</math> is an example of a [[functional equation]] — an equation to be solved for the function <math>f</math> for all values of <math>z</math>. It is analogous to the recurrence satisfied by factorials, <math>n!=n(n-1)!</math>, the only difference being that the function argument has been shifted by 1. A repeated application of the gamma function's recurrence formula gives | |||
:<math>\Gamma(z+n)=z(z+1)(z+2)\cdots(z+n-1)\Gamma(z),</math> | |||
which together with the initial value <math>\textstyle \Gamma(1)=\int_{0}^{\infty}e^{-t}dt=1</math> establishes that | |||
:<math>n | :<math>\Gamma(n)=1\cdot2\cdot3\ldots(n-1)=(n-1)!</math> | ||
for positive integers <math>n</math>. We can of course equivalently write <math>\Gamma(n+1)=n!</math>. We may use these formulas to explicitly calculate <math>\Gamma(n)</math> or, conversely, to define <math>z!</math> for non-integers in terms of the gamma function. | |||
===Real and complex numbers=== | |||
The behavior of <math>\Gamma(z)</math> for an increasing positive variable is simple: it grows quickly — faster than an exponential function. Asymptotically as <math>z\to\infty</math>, the magnitude of the gamma function is given by [[Stirling's formula]] | |||
:<math>\Gamma(z+1)\sim\sqrt{2\pi z}\left(\frac{z}{e}\right)^{z},</math> | |||
where the symbol ~ means that the quotient of both sides converges to 1. | |||
The behavior for nonpositive ''z'' is more intricate. Euler's integral does not converge for ''z'' ≤ 0, but the function it defines in the positive complex half-plane has a unique [[analytic continuation]] to the negative half-plane. One way to find that analytic continuation is to use Euler's integral for positive arguments and extend the domain to negative numbers by repeated application of the recurrence formula, | |||
does not | |||
:<math>\Gamma(z)=\frac{\Gamma(z+n)}{z(z+1)\cdots(z+n-1)},</math> | :<math>\Gamma(z)=\frac{\Gamma(z+n)}{z(z+1)\cdots(z+n-1)},</math> | ||
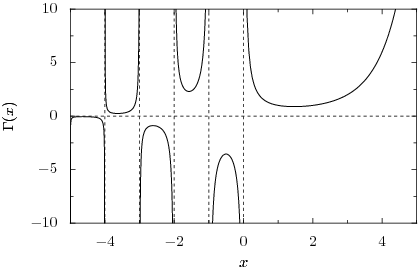
choosing ''n'' such that ''z'' + ''n'' is positive. The product in the denominator is zero when ''z'' equals any of the integers 0, −1, −2,... . Thus, the gamma function must be undefined at those points due to division by zero; it is a [[meromorphic function]] with [[pole (complex analysis)|pole]]s at the nonpositive integers. The following image shows the graph of the gamma function along the real line: | |||
[[Image:Gamma function.png|center]] | [[Image:Gamma function.png|center]] | ||
The gamma function is nonzero everywhere along the real line, although it comes arbitrarily close as <math>z\to-\infty</math>. There is in fact no complex number ''z'' for which <math>\Gamma(z) = 0</math>, and hence the ''reciprocal gamma function'' <math>1/\Gamma</math> is an [[entire function]], with zeros at | The gamma function is nonzero everywhere along the real line, although it comes arbitrarily close as <math>z\to-\infty</math>. There is in fact no complex number ''z'' for which <math>\Gamma(z) = 0</math>, and hence the ''reciprocal gamma function'' <math>1/\Gamma</math> is an [[entire function]], with zeros at ''z'' = 0, −1, −2,.... We see that the gamma function has a local minimum at <math>x_{\mathrm{min}}\approx1.46163</math> where it attains the value <math>\Gamma(x_{\mathrm{min}})\approx0.885603</math>. The gamma function must alternate sign between the poles because the product in the forward recurrence contains an odd number of negative factors if the number of poles between <math>z</math> and <math>z+n</math> is odd, and an even number if the number of poles is even. | ||
Plotting the gamma function in the complex plane yields beautiful graphs: | Plotting the gamma function in the complex plane yields beautiful graphs: | ||
<center> | |||
<gallery> | <gallery> | ||
Image:Complex gamma function abs.png|Absolute value | Image:Complex gamma function abs.png|Absolute value | ||
| Line 107: | Line 65: | ||
Image:Complex gamma function Im.png|Imaginary part | Image:Complex gamma function Im.png|Imaginary part | ||
</gallery> | </gallery> | ||
</center> | |||
===Reflection and rational arguments=== | |||
The recurrence relation is not the only functional equation satisfied by the gamma function. Another important property is the ''reflection formula'' | |||
:<math>\Gamma(z)\Gamma(1-z)=\frac{\pi}{\sin\pi z}</math> | :<math>\Gamma(z)\Gamma(1-z)=\frac{\pi}{\sin\pi z}</math> | ||
| Line 118: | Line 79: | ||
Hence, by the recurrence formula, the gamma function or factorial of any half-integer is a rational multiple of <math>\sqrt{\pi}</math>. | Hence, by the recurrence formula, the gamma function or factorial of any half-integer is a rational multiple of <math>\sqrt{\pi}</math>. | ||
[[ | There are many cases in which products or quotients of the gamma function can be evaluated. For example, it follows from the recurrence relation that <math>\Gamma(r+n)/\Gamma(r)</math> is a rational function of <math>r</math> whenever <math>n</math> is an integer, and a rational number whenever <math>r</math> is rational.<ref>Assuming that no poles are encountered</ref> A third functional equation is the ''[[multiplication theorem]]'' | ||
:<math>n | :<math>\prod_{n=0}^{k-1} \Gamma\left(z+\frac{n}{k}\right) = (2 \pi)^{(k-1)/2} \; k^{1/2 - kz} \; \Gamma(kz),</math> | ||
which | of which the ''duplication formula'' | ||
:<math> | :<math> | ||
\Gamma(z) \; \Gamma\left(z + \frac{1} | \Gamma(z) \; \Gamma\left(z + \frac{1}{2}\right) = 2^{1-2z} \; \sqrt{\pi} \; \Gamma(2z), \,\! | ||
</math> | </math> | ||
is a special case. | |||
From the multiplicative properties of the gamma function, it is possible to derive exotic-looking results such as | |||
:<math>2 \pi = \sqrt 3 \; | :<math>2 \pi = \sqrt 3 \; | ||
| Line 152: | Line 103: | ||
</math> | </math> | ||
It might be tempting to generalize the result that <math>\Gamma(1/2) = \sqrt \pi</math> by looking for a formula for other individual values <math>\Gamma(r)</math> where <math>r</math> is rational. However, these numbers are not known to be expressible by themselves in terms of elementary functions. It has been proved that <math>\Gamma(n+r)</math> is a transcendental number and [[algebraic independence|algebraically independent]] of <math>\pi</math> for any integer <math>n</math> and each of the fractions <math>r</math> = 1/6, 1/4, 1/3, 2/3, 3/4, and 5/6.<ref>Waldschmidt, M. (2006). "[http://www.math.jussieu.fr/~miw/articles/pdf/TranscendencePeriods.pdf Transcendence of Periods: The State of the Art]". ''Pure and Applied Mathematics Quarterly'', Volume 2, Number 2, 435—463 (PDF copy published by the author)</ref> In general, when computing values of the gamma function, we must settle for numerical approximations. | |||
===Numerical methods=== | |||
It is easy to approximate the gamma function given a known approximation that holds on some interval of unit width, say for <math>1 \le z \le 2</math>; the value anywhere else can then be computed via the recurrence and reflection formulas, using only a few multiplications or an evaluation of the sine in the reflection formula. Listings of [[polynomial]]s and [[rational function]]s that approximate the gamma function in a unit interval are available in various reference works.<ref>For instance, ''Abramowitz & Stegun'', [http://www.math.sfu.ca/~cbm/aands/page_257.htm page 257]</ref> | |||
For large arguments, say <math>|z| > 10</math>, it is best to use an asymptotic expansion; the most popular is ''Stirling's series'' | |||
:<math>\Gamma(z+1) \sim \sqrt{2\pi z}\left(\frac{z}{e}\right)^{z}\left(1+\frac{1}{12z}+\frac{1}{288z^{2}}-\cdots\right).</math> | |||
This is Stirling's formula multiplied by a series that corrects the error. The series coefficients can be calculated in terms of [[Bernoulli number]]s. The "<math>\sim</math>" sign denotes an asymptotic equality: the series diverges for every ''z'', but yields arbitrarily accurate approximations of the gamma function as <math>z\to+\infty</math> if the series is truncated at the smallest term. We can use Stirling's series to calculate the gamma function for small numbers as well, using the recurrence relation. Taking <math>n=10</math> and calculating <math>\Gamma(z)</math> from <math>\Gamma(z+n)</math>, using the three first terms in Stirling's series, we obtain <math>\Gamma(1)</math> ≈ 1.000003 and <math>\Gamma(2)</math> ≈ 1.000002; this particular approximation is good to five decimal places on the interval <math>1 \le z \le 2</math>. With larger <math>n</math> and more terms, Stirling's series permits calculating the gamma function with arbitrary precision. | |||
Other practical methods for high-precision calculation include the [[Lanczos approximation]] and [[Spouge's approximation]], which are both similar in form to Stirling's series but have different convergence characteristics. | |||
It should be noted that it may be convenient to work with the logarithm of the gamma function instead of the gamma function itself, since the raw gamma function grows quickly and can cause overflow in computer arithmetic. It is common to encounter a quotient of two large gamma function values, which is most safely computed by subtracting two logarithms. Stirling's, Lanczos's and Spouge's approximations can all be calculated directly in logarithmic form. | |||
==Applications== | |||
Opening a random page in an advanced table of formulas, one may be as likely to spot the gamma function as a trigonometric function. One author describes the gamma function as "Arguably, the most common special function, or the least 'special' of them. The other transcendental functions listed below are called 'special' because you could conceivably avoid some of them by staying away from many specialized mathematical topics. On the other hand, the Gamma function <math>y = \Gamma(x)</math> is most difficult to avoid."<ref>Michon, G. P. "[http://home.att.net/~numericana/answer/functions.htm Trigonometry and Basic Functions]". ''Numericana''. Retrieved May 5, 2007.</ref> | |||
===Integration problems=== | |||
The gamma function finds application in such diverse areas as [[quantum physics]], [[astrophysics]] and [[fluid dynamics]].<ref>Chaudry, M. A. & Zubair, S. M. (2001). ''On A Class of Incomplete Gamma Functions with Applications''. p. 37</ref> The [[gamma distribution]], which is formulated in terms of the gamma function, is used in [[statistics]] to model a wide range of processes; for example, the time between occurrences of earthquakes.<ref>Rice, J. A. (1995). ''Mathematical Statistics and Data Analysis'' (Second Edition). p. 52–53</ref> | |||
The primary reason for the gamma function's usefulness in such contexts is the prevalence of expressions of the type <math>f(t)\,e^{-g(t)}</math> which describe processes that decay exponentially in time or space. Integrals of such expressions can occasionally be solved in terms of the gamma function when no elementary solution exists. For example, if <math>f</math> is a power function and <math>g</math> is a linear function, a simple change of variables gives the evaluation | |||
:<math>\int_0^\infty t^b e^{-at} \,dt = \frac{\Gamma(a+1)}{a^{b+1}}.</math> | |||
The fact that the integration is performed along the entire positive real line might signify that the gamma function describes the cumulation of a time-dependent process that continues indefinitely, or the value might be the total of a distribution in an infinite space. | |||
It is of course frequently useful to take limits of integration other than 0 and <math>\infty</math> to describe the cumulation of a finite process, in which case the ordinary gamma function is no longer a solution; the solution is then called an [[incomplete gamma function]]. (The ordinary gamma function, obtained by integrating across the entire positive real line, is sometimes called the ''complete gamma function'' for contrast). | |||
An important category of exponentially decaying functions is that of [[Gaussian function]]s <math>ae^{-(x-b)^2/c^2}</math> and integrals thereof, such as the [[error function]]. There are many interrelations between these functions and the gamma function; notably, the square root of <math>\pi</math> we obtained by evaluating <math>\Gamma(1/2)</math> is the "same" as that found in the normalizing factor of the error function and the [[normal distribution]]. | |||
The integrals we have discussed so far involve transcendental functions, but the gamma function also arises from integrals of purely algebraic functions. In particular, the [[arc length]]s of [[ellipse]]s and of the [[lemniscate]], which are curves defined by algebraic equations, are given by [[elliptic integral]]s that in special cases can be evaluated in terms of the gamma function. The gamma function can also be used to calculate "volume" and "area" of <math>n</math>-dimensional [[hypersphere]]s. | |||
Another important special case is that of the [[beta function]] | |||
:<math>\mathrm{\Beta}(x,y) = \int_0^1 t^{x-1}(1-t)^{y-1}\,dt = \frac{\Gamma(x)\,\Gamma(y)}{\Gamma(x+y)}.</math> | |||
== | ===Calculating products=== | ||
The gamma function's ability to and generalize factorial products immediately leads to applications in many areas of mathematics; in [[combinatorics]], and by extension in areas such as [[probability theory]] and the calculation of [[power series]]. Many expressions involving products of successive integers can be written as some combination of factorials, the most important example perhaps being that of the [[binomial coefficient]] | |||
:<math>{n \choose k} = \frac{n!}{k!(n-k)!}.</math> | |||
The example of binomial coefficients motivates why the properties of the gamma function when extended to negative numbers are natural. A binomial coefficient gives the number of ways to choose <math>k</math> elements from a set of <math>n</math> elements; if <math>k > n</math>, there are of course no ways. If <math>k > n</math>, <math>(n-k)!</math> is the factorial of a negative integer and hence infinite if we use the gamma function definition of factorials — dividing by infinity gives the expected value of 0. | |||
We can replace the factorial by a gamma function to extend any such formula to the complex numbers. Generally, this works for any product wherein each factor is a [[rational function]] of the index variable, by factoring the rational function into linear expressions. If <math>P</math> and <math>Q</math> are monic polynomials of degree <math>m</math> and <math>n</math> with respective roots <math>p_1 \ldots p_m</math> and <math>q_1 \ldots q_n</math>, we have | |||
:<math>\prod_{i=a}^b \frac{P(i)}{Q(i)} = \left( \prod_{j=1}^m \frac{\Gamma(b-p_j+1)}{\Gamma(a-p_j)} \right) \left( \prod_{k=1}^n \frac{\Gamma(a-q_k)}{\Gamma(b-q_k+1)} \right).</math> | |||
If we have a way to calculate the gamma function numerically, it is a breeze to calculate numerical values of such products. The number of gamma functions in the right-hand side depends only on the degree of the polynomials, so it does not matter whether <math>b-a</math> equals 5 or <math>10^5</math>. Moreover, due to the poles of the gamma function, the equation also holds (in the sense of taking limits) when the left-hand product contain zeros or poles. | |||
By taking limits, certain rational products with infinitely many factors can be evaluated in terms of the gamma function as well. Due to the [[Weierstrass factorization theorem]], analytic functions can be written as infinite products, and these can sometimes be represented as finite products or quotients of the gamma function. We have already seen one striking example: the reflection formula essentially represents the sine function as the product of two gamma functions. Starting from this formula, the exponential function as well as all the trigonometric and hyperbolic functions can be expressed in terms of the gamma function. | |||
More functions yet, including the [[hypergeometric function]] and special cases thereof, can be represented by means of complex [[contour integral]]s of products and quotients of the gamma function, called [[Mellin-Barnes integral]]s. | |||
===Analytic number theory=== | |||
An elegant and deep application of the gamma function is in the study of the [[Riemann zeta function]]. A fundamental property of the Riemann zeta function is its [[functional equation]]: | |||
:<math>\ | :<math>\Gamma\left(\frac{s}{2}\right)\zeta(s)\pi^{-s/2} = \Gamma\left(\frac{1-s}{2}\right)\zeta(1-s)\pi^{-(1-s)/2}.</math> | ||
Among other things, this provides an explicit form for the [[analytic continuation]] of the zeta function to a meromorphic function in the complex plane and leads to an immediate proof that the zeta function has infinitely many so-called "trivial" zeros on the real line. Borwein ''et al''. call this formula "one of the most beautiful findings in mathematics".<ref>{{cite book | author = Borwein, J., Bailey, D. H. & Girgensohn, R. | date = 2003 | title = Experimentation in Mathematics | publisher = A. K. Peters | pages = 133 | isbn = 1-56881-136-5}}</ref> Another champion for that title might be | |||
:<math>\zeta(z) \; \Gamma(z) = \int_0^\infty \frac{t^{z-1}}{e^t-1} \; dt.</math> | |||
Both formulas were derived by [[Bernhard Riemann]] in his seminal 1859 paper "Über die Anzahl der Primzahlen unter einer gegebenen Grösse" ("On the Number of Prime Numbers less than a Given Quantity"), one of the milestones in the development of [[analytic number theory]] — the branch of mathematics that studies [[prime number]]s using the tools of mathematical analysis. Factorial numbers, considered as discrete objects, are an important concept in classical number theory because they contain many prime factors, but Riemann found a use for their continuous extension that arguably turned out to be even more important. | |||
==History== | |||
The gamma function has caught the interest of some of the most prominent mathematicians of all time. Its history, notably documented by [[Philip J. Davis]] in an article that won him the 1963 [[Chauvenet Prize]], reflects many of the major developments within mathematics since the 18th century. In the words of Davis, "each generation has found something of interest to say about the gamma function. Perhaps the next generation will also."<ref name="Davis">Davis, P. J. (1959). "Leonhard Euler's Integral: A Historical Profile of the Gamma Function", ''The American Mathematical Monthly'', Vol. 66, No. 10 (Dec., 1959), pp. 849-869</ref> | |||
===18th century: Euler and Stirling=== | |||
: | |||
[[Image:Euler factorial paper.png|thumb|250px|The first page of Euler's paper "De progressionibus transcendentibus seu quarum termini generales algebraice dari nequeunt".]] | |||
The problem of extending the factorial to non-integer arguments was apparently first considered by [[Daniel Bernoulli]] and [[Christian Goldbach]] in the 1720s, and was solved at the end of the same decade by Leonhard Euler. Euler gave two different definitions: the first was not his integral but an [[infinite product]], | |||
:<math>n! = \prod_{k=1}^\infty \frac{\left(1+\frac{1}{k}\right)^n}{1+\frac{n}{k}},</math> | |||
of which he informed Goldbach in a letter dated October 13, 1729. He wrote to Goldbach again on January 8, 1730, to announce his discovery of the integral representation | |||
= | :<math>n!=\int_{0}^{1}(-\log s)^{n}\, ds,</math> | ||
which is valid for <math>n>0</math>. By the change of variables <math>t = -\log s</math>, this becomes the familiar Euler integral. Euler published his results in the paper "De progressionibus transcendentibus seu quarum termini generales algebraice dari nequeunt" ("On transcendental progressions, that is, those whose general terms cannot be given algebraically"), submitted to the [[St. Petersburg Academy]] on November 28, 1729.<ref>Euler's paper was published in ''Commentarii academiae scientiarum Petropolitanae'' 5, 1738, 36—57. See [http://math.dartmouth.edu/~euler/pages/E019.html E19 -- De progressionibus transcendentibus seu quarum termini generales algebraice dari nequeunt], from The Euler | |||
Archive, which includes a scanned copy of the original article. An [http://home.sandiego.edu/~langton/eg.pdf English translation] by S. Langton is also available.</ref> Euler further discovered some of the gamma function's important functional properties, including the reflection formula. | |||
[[James Stirling]], a contemporary of Euler, also attempted to find a continuous expression for the factorial and came up with what is now known as Stirling's formula. Although Stirling's formula gives a good estimate of <math>n!</math>, also for non-integers, it does not provide the exact value. Extensions of his formula that correct the error were given by Stirling himself and by [[Jacques Philippe Marie Binet]]. | |||
: | ===19th century: Gauss, Weierstrass and Legendre=== | ||
[[Carl Friedrich Gauss]] rewrote Euler's product as | |||
:<math>\ | :<math>\Gamma(z) = \lim_{m\to\infty}\frac{m^{z}m!}{z(z+1)(z+2)\cdots(z+m)}</math> | ||
and used this formula to discover new properties of the gamma function. Although Euler was a pioneer in the theory of complex variables, he does not appear to have considered the factorial of a complex number, as instead Gauss first did.<ref name="Remmert">{{cite book | author = Remmert, R., Kay, L. D. (translator) | title = Classical Topics in Complex Function Theory | publisher = Springer | date = 2006 | isbn = 0387982213}}</ref> Gauss also proved the [[multiplication theorem]] of the gamma function and investigated the connection between the gamma function and elliptic integrals. | |||
[[Karl Weierstrass]] further established the role of the gamma function in [[complex analysis]], starting from yet another product representation, | |||
:<math>\Gamma(z) = \frac{e^{-\gamma z}}{z} \prod_{k=1}^\infty \left(1 + \frac{z}{k}\right)^{-1} e^{z/k}, \,\!</math> | |||
where <math>\gamma \approx 0.577216</math> is [[Euler's constant]]. Weierstrass originally wrote his product as one for <math>1/\Gamma</math>, in which case it is taken over the function's zeros rather than its poles. Inspired by this result, he proved what is known as the [[Weierstrass factorization theorem]] — that any entire function can be written as a product over its zeros in the complex plane; a generalization of the [[fundamental theorem of algebra]]. | |||
The gamma function | The name gamma function and the symbol <math>\Gamma</math> were introduced by [[Adrien-Marie Legendre]] around 1811; Legendre also rewrote Euler's integral definition in its modern form. Although the symbol is an upper-case Greek Gamma, there is no accepted standard for whether the function name should be written "Gamma function" or "gamma function" (some authors simply write "<math>\Gamma</math>-function"). The alternative "Pi function" notation <math>\Pi(z)=z!</math> due to Gauss is sometimes encountered in older literature, but Legendre's notation is dominant in modern works. | ||
It is justified to ask why we distinguish between the "ordinary factorial" and the gamma function by using distinct symbols, and particularly why the gamma function should be normalized to <math>\Gamma(n+1)=n!</math> instead of simply using "<math>\Gamma(n)=n!</math>". Legendre's motivation for the normalization | |||
does not appear to be known, and has been criticized as cumbersome by some (the 20th-century mathematician [[Cornelius Lanczos]], for example, called it "void of any rationality" and would instead use <math>z!</math><ref>Lanczos, C. (1964). "A precision approximation of the gamma function." J. SIAM Numer. Anal. Ser. B, Vol. 1.</ref>). The normalization does simplify some formulas, but complicates others. | |||
: | ===19th-20th centuries: characterizing the gamma function=== | ||
It is somewhat problematic that a large number of definitions have been given for the gamma function. Although they describe the same function, it is not entirely straightforward to prove the equivalence. Stirling never proved that his extended formula corresponds exactly to Euler's gamma function; a proof was first given by [[Charles Hermite]] in 1900.<ref name="Knuth">{{cite book | author = Knuth, D. E. | title = The Art of Computer Programming, volume 1 (Fundamental Algorithms) | publisher = Addison-Wesley | date = 1997}}</ref> Instead of finding a specialized proof for each formula, it would be desirable to have a general method of identifying the gamma function. | |||
One way to prove would be to find a [[differential equation]] that characterizes the gamma function. Most special functions in applied mathematics arise as solutions to differential equations, whose solutions are unique. However, the gamma function does not appear to satisfy any simple differential equation. [[Otto Hölder]] proved in 1887 that the gamma function at least does not satisfy any [[algebraic differential equation|''algebraic'' differential equation]] by showing that a solution to such an equation could not satisfy the gamma function's recurrence formula. This result is known as [[Hölder's theorem]]. | |||
A definite and generally applicable characterization of the gamma function was not given until 1922. [[Harald Bohr]] and [[Johannes Mollerup]] then proved what is known as the ''[[Bohr-Mollerup theorem]]'': that the gamma function is the unique solution to the factorial recurrence relation that is positive and ''[[logarithmic convexity|logarithmically convex]]'' for positive ''z'' and whose value at 1 is 1 (a function is logarithmically convex if its logarithm is convex). | |||
The Bohr-Mollerup theorem is useful because it is relatively easy to prove logarithmic convexity for any of the different formulas used to define the gamma function. Taking things further, instead of defining the gamma function by any particular formula, we can choose the conditions of the Bohr-Mollerup theorem as the definition, and then pick any formula we like that satisfies the conditions as a starting point for studying the gamma function. This approach was used by the [[Bourbaki group]]. | |||
===Reference tables and software=== | |||
Although the gamma function can be calculated virtually as easily as any mathematically simpler function with a modern computer — even with a programmable pocket calculator — this was of course not always the case. Until the mid-20th century, mathematicians relied on hand-made tables; in the case of the gamma function, notably a table computed by Gauss in 1813 and one computed by Legendre in 1825. | |||
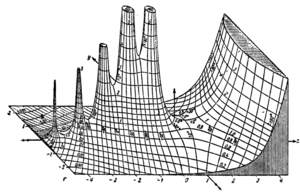
: | [[Image:Jahnke gamma function.png|thumb|300px|A hand-drawn graph of the absolute value of the complex gamma function, from ''Tables of Higher Functions'' by Jahnke and Emde.]] | ||
Tables of complex values of the gamma function, as well as hand-drawn graphs, were given in ''Tables of Higher Functions'' by Jahnke and Emde, first published in Germany in 1909. According to [[Michael Berry]], "the publication in J&E of a three-dimensional graph showing the poles of the gamma function in the complex plane acquired an almost iconic status."<ref>Berry, M. "[http://www.physicstoday.org/pt/vol-54/iss-4/p11.html Why are special functions special?]". ''Physics Today'', April 2001</ref> | |||
There was in fact little practical need for anything but real values of the gamma function until the 1930s, when applications for the complex gamma function were discovered in theoretical physics. As electronic computers became available for the production of tables in the 1950s, several extensive tables for the complex gamma function were published to meet the demand, including a table accurate to 12 decimal places from the U.S. [[National Bureau of Standards]].<ref name=Davis /> | |||
Like for many other special functions, ''[[Abramowitz and Stegun]]'' became the standard reference after its publication in 1964. | |||
Double-precision floating-point implementations of the gamma function and its logarithm are now available in most scientific computing software and special functions libraries, for example [[Matlab]], [[GNU Octave]], and the [[GNU Scientific Library]]. The gamma function was also added to the [[C (programming language)|C]] mathematics library (math.h) as part of the C99 standard, but is not implemented by all C compilers. Arbitrary-precision implementations are available in most [[computer algebra system]]s, such as [[Mathematica]] and [[Maple]]. [[Pari/GP]], [[MPFR]] and [[MPFUN]] contain free arbitrary-precision implementations. | |||
[[Category: | ==Notes and references== | ||
<references/>[[Category:Suggestion Bot Tag]] | |||
Latest revision as of 06:01, 20 August 2024
The gamma function is a mathematical function that extends the domain of factorials to non-integers. The factorial of a positive integer n, written n!, is the product 1·2·3···n. The gamma function, denoted by , is defined to satisfy for all positive integers n and to smoothly interpolate the factorial between the integers. The gamma function is one of the most commonly occurring examples of a nonelementary function; that is, a function that cannot be expressed in finite terms using algebraic operations, exponentials, and logarithms. Its study dates back to Leonhard Euler, who gave a formula for its calculation in 1729.
Motivation
The gamma function can be seen as a solution to the following interpolation problem: find a smooth curve that connects the points given by at the positive integers. A plot of the first few factorials makes clear that such a curve can be drawn (for example by hand), but it would be preferable to have a formula that precisely describes the curve. The formula for the factorial cannot be used directly for fractional values of since the number of factors depends on and only is valid when is an integer. The solution would have to be a closed-form expression, in which the number of operations does not depend on the size of .
There is a quite analogous problem for which the solution is simple. A famous anecdote goes that Carl Friedrich Gauss, as a child, found that the sum can be calculated as and that he thereby was able to quickly sum all the integers between 1 and 100, to the astonishment of his teacher. The formula is of course valid for fractional values of and describes the simple shape known as a parabola.
The analogy is that simply changing the "+" sign in to a "" gives the factorial interpolation problem; however, Gauss's closed-form solution to the one problem cannot be translated to the other. There is in fact no such simple solution for factorials. Any combination of sums, products, powers, exponential functions or logarithms with a fixed number of terms will not suffice to express : with more precise terminology, the factorial is not an elementary function. But it is possible to find a general formula for factorials with some more work, by deploying tools such as integrals and limits from calculus. It is this non-elementary solution that is called the gamma function.
It must be noted that there are actually infinitely many extensions of the factorial to non-integers (each of them non-elementary): infinitely many curves can be drawn through any set of isolated points. The gamma function is distinguished by uncontestedly being the most useful solution in practice. The question of the gamma function's uniqueness will be discussed in more detail later on; we will first give the exact definition of the gamma function and state its fundamental properties.
Basic properties of the gamma function
Euler's integral definition
The gamma function is commonly defined by a definite integral due to Leonhard Euler,
where is interpreted as if is not an integer.[1] Using standard theorems from mathematical analysis, it can be shown that Euler's integral defines to be a continuous function if is positive. In fact, Euler's integral is valid for any complex number with a positive real part and defines the gamma function to be an analytic function in the positive complex half-plane.[2]
To see that the gamma function corresponds to the factorial at integers, we can insert instead of and perform an integration by parts to obtain
This relation is called the recurrence formula or recurrence relation of the gamma function. The equation is an example of a functional equation — an equation to be solved for the function for all values of . It is analogous to the recurrence satisfied by factorials, , the only difference being that the function argument has been shifted by 1. A repeated application of the gamma function's recurrence formula gives
which together with the initial value establishes that
for positive integers . We can of course equivalently write . We may use these formulas to explicitly calculate or, conversely, to define for non-integers in terms of the gamma function.
Real and complex numbers
The behavior of for an increasing positive variable is simple: it grows quickly — faster than an exponential function. Asymptotically as , the magnitude of the gamma function is given by Stirling's formula
where the symbol ~ means that the quotient of both sides converges to 1.
The behavior for nonpositive z is more intricate. Euler's integral does not converge for z ≤ 0, but the function it defines in the positive complex half-plane has a unique analytic continuation to the negative half-plane. One way to find that analytic continuation is to use Euler's integral for positive arguments and extend the domain to negative numbers by repeated application of the recurrence formula,
choosing n such that z + n is positive. The product in the denominator is zero when z equals any of the integers 0, −1, −2,... . Thus, the gamma function must be undefined at those points due to division by zero; it is a meromorphic function with poles at the nonpositive integers. The following image shows the graph of the gamma function along the real line:
The gamma function is nonzero everywhere along the real line, although it comes arbitrarily close as . There is in fact no complex number z for which , and hence the reciprocal gamma function is an entire function, with zeros at z = 0, −1, −2,.... We see that the gamma function has a local minimum at where it attains the value . The gamma function must alternate sign between the poles because the product in the forward recurrence contains an odd number of negative factors if the number of poles between and is odd, and an even number if the number of poles is even.
Plotting the gamma function in the complex plane yields beautiful graphs:
Reflection and rational arguments
The recurrence relation is not the only functional equation satisfied by the gamma function. Another important property is the reflection formula
which gives a concise relation between the gamma function of positive and negative numbers. The division by a sine, which is periodically zero, again indicates the existence of the gamma function's periodically occurring poles. Further, inserting z = 1/2 reveals the surprising fact that
Hence, by the recurrence formula, the gamma function or factorial of any half-integer is a rational multiple of .
There are many cases in which products or quotients of the gamma function can be evaluated. For example, it follows from the recurrence relation that is a rational function of whenever is an integer, and a rational number whenever is rational.[3] A third functional equation is the multiplication theorem
of which the duplication formula
is a special case.
From the multiplicative properties of the gamma function, it is possible to derive exotic-looking results such as
It might be tempting to generalize the result that by looking for a formula for other individual values where is rational. However, these numbers are not known to be expressible by themselves in terms of elementary functions. It has been proved that is a transcendental number and algebraically independent of for any integer and each of the fractions = 1/6, 1/4, 1/3, 2/3, 3/4, and 5/6.[4] In general, when computing values of the gamma function, we must settle for numerical approximations.
Numerical methods
It is easy to approximate the gamma function given a known approximation that holds on some interval of unit width, say for ; the value anywhere else can then be computed via the recurrence and reflection formulas, using only a few multiplications or an evaluation of the sine in the reflection formula. Listings of polynomials and rational functions that approximate the gamma function in a unit interval are available in various reference works.[5]
For large arguments, say , it is best to use an asymptotic expansion; the most popular is Stirling's series
This is Stirling's formula multiplied by a series that corrects the error. The series coefficients can be calculated in terms of Bernoulli numbers. The "" sign denotes an asymptotic equality: the series diverges for every z, but yields arbitrarily accurate approximations of the gamma function as if the series is truncated at the smallest term. We can use Stirling's series to calculate the gamma function for small numbers as well, using the recurrence relation. Taking and calculating from , using the three first terms in Stirling's series, we obtain ≈ 1.000003 and ≈ 1.000002; this particular approximation is good to five decimal places on the interval . With larger and more terms, Stirling's series permits calculating the gamma function with arbitrary precision.
Other practical methods for high-precision calculation include the Lanczos approximation and Spouge's approximation, which are both similar in form to Stirling's series but have different convergence characteristics.
It should be noted that it may be convenient to work with the logarithm of the gamma function instead of the gamma function itself, since the raw gamma function grows quickly and can cause overflow in computer arithmetic. It is common to encounter a quotient of two large gamma function values, which is most safely computed by subtracting two logarithms. Stirling's, Lanczos's and Spouge's approximations can all be calculated directly in logarithmic form.
Applications
Opening a random page in an advanced table of formulas, one may be as likely to spot the gamma function as a trigonometric function. One author describes the gamma function as "Arguably, the most common special function, or the least 'special' of them. The other transcendental functions listed below are called 'special' because you could conceivably avoid some of them by staying away from many specialized mathematical topics. On the other hand, the Gamma function is most difficult to avoid."[6]
Integration problems
The gamma function finds application in such diverse areas as quantum physics, astrophysics and fluid dynamics.[7] The gamma distribution, which is formulated in terms of the gamma function, is used in statistics to model a wide range of processes; for example, the time between occurrences of earthquakes.[8]
The primary reason for the gamma function's usefulness in such contexts is the prevalence of expressions of the type which describe processes that decay exponentially in time or space. Integrals of such expressions can occasionally be solved in terms of the gamma function when no elementary solution exists. For example, if is a power function and is a linear function, a simple change of variables gives the evaluation
The fact that the integration is performed along the entire positive real line might signify that the gamma function describes the cumulation of a time-dependent process that continues indefinitely, or the value might be the total of a distribution in an infinite space.
It is of course frequently useful to take limits of integration other than 0 and to describe the cumulation of a finite process, in which case the ordinary gamma function is no longer a solution; the solution is then called an incomplete gamma function. (The ordinary gamma function, obtained by integrating across the entire positive real line, is sometimes called the complete gamma function for contrast).
An important category of exponentially decaying functions is that of Gaussian functions and integrals thereof, such as the error function. There are many interrelations between these functions and the gamma function; notably, the square root of we obtained by evaluating is the "same" as that found in the normalizing factor of the error function and the normal distribution.
The integrals we have discussed so far involve transcendental functions, but the gamma function also arises from integrals of purely algebraic functions. In particular, the arc lengths of ellipses and of the lemniscate, which are curves defined by algebraic equations, are given by elliptic integrals that in special cases can be evaluated in terms of the gamma function. The gamma function can also be used to calculate "volume" and "area" of -dimensional hyperspheres.
Another important special case is that of the beta function
Calculating products
The gamma function's ability to and generalize factorial products immediately leads to applications in many areas of mathematics; in combinatorics, and by extension in areas such as probability theory and the calculation of power series. Many expressions involving products of successive integers can be written as some combination of factorials, the most important example perhaps being that of the binomial coefficient
The example of binomial coefficients motivates why the properties of the gamma function when extended to negative numbers are natural. A binomial coefficient gives the number of ways to choose elements from a set of elements; if , there are of course no ways. If , is the factorial of a negative integer and hence infinite if we use the gamma function definition of factorials — dividing by infinity gives the expected value of 0.
We can replace the factorial by a gamma function to extend any such formula to the complex numbers. Generally, this works for any product wherein each factor is a rational function of the index variable, by factoring the rational function into linear expressions. If and are monic polynomials of degree and with respective roots and , we have
If we have a way to calculate the gamma function numerically, it is a breeze to calculate numerical values of such products. The number of gamma functions in the right-hand side depends only on the degree of the polynomials, so it does not matter whether equals 5 or . Moreover, due to the poles of the gamma function, the equation also holds (in the sense of taking limits) when the left-hand product contain zeros or poles.
By taking limits, certain rational products with infinitely many factors can be evaluated in terms of the gamma function as well. Due to the Weierstrass factorization theorem, analytic functions can be written as infinite products, and these can sometimes be represented as finite products or quotients of the gamma function. We have already seen one striking example: the reflection formula essentially represents the sine function as the product of two gamma functions. Starting from this formula, the exponential function as well as all the trigonometric and hyperbolic functions can be expressed in terms of the gamma function.
More functions yet, including the hypergeometric function and special cases thereof, can be represented by means of complex contour integrals of products and quotients of the gamma function, called Mellin-Barnes integrals.
Analytic number theory
An elegant and deep application of the gamma function is in the study of the Riemann zeta function. A fundamental property of the Riemann zeta function is its functional equation:
Among other things, this provides an explicit form for the analytic continuation of the zeta function to a meromorphic function in the complex plane and leads to an immediate proof that the zeta function has infinitely many so-called "trivial" zeros on the real line. Borwein et al. call this formula "one of the most beautiful findings in mathematics".[9] Another champion for that title might be
Both formulas were derived by Bernhard Riemann in his seminal 1859 paper "Über die Anzahl der Primzahlen unter einer gegebenen Grösse" ("On the Number of Prime Numbers less than a Given Quantity"), one of the milestones in the development of analytic number theory — the branch of mathematics that studies prime numbers using the tools of mathematical analysis. Factorial numbers, considered as discrete objects, are an important concept in classical number theory because they contain many prime factors, but Riemann found a use for their continuous extension that arguably turned out to be even more important.
History
The gamma function has caught the interest of some of the most prominent mathematicians of all time. Its history, notably documented by Philip J. Davis in an article that won him the 1963 Chauvenet Prize, reflects many of the major developments within mathematics since the 18th century. In the words of Davis, "each generation has found something of interest to say about the gamma function. Perhaps the next generation will also."[10]
18th century: Euler and Stirling
The problem of extending the factorial to non-integer arguments was apparently first considered by Daniel Bernoulli and Christian Goldbach in the 1720s, and was solved at the end of the same decade by Leonhard Euler. Euler gave two different definitions: the first was not his integral but an infinite product,
of which he informed Goldbach in a letter dated October 13, 1729. He wrote to Goldbach again on January 8, 1730, to announce his discovery of the integral representation
which is valid for . By the change of variables , this becomes the familiar Euler integral. Euler published his results in the paper "De progressionibus transcendentibus seu quarum termini generales algebraice dari nequeunt" ("On transcendental progressions, that is, those whose general terms cannot be given algebraically"), submitted to the St. Petersburg Academy on November 28, 1729.[11] Euler further discovered some of the gamma function's important functional properties, including the reflection formula.
James Stirling, a contemporary of Euler, also attempted to find a continuous expression for the factorial and came up with what is now known as Stirling's formula. Although Stirling's formula gives a good estimate of , also for non-integers, it does not provide the exact value. Extensions of his formula that correct the error were given by Stirling himself and by Jacques Philippe Marie Binet.
19th century: Gauss, Weierstrass and Legendre
Carl Friedrich Gauss rewrote Euler's product as
and used this formula to discover new properties of the gamma function. Although Euler was a pioneer in the theory of complex variables, he does not appear to have considered the factorial of a complex number, as instead Gauss first did.[12] Gauss also proved the multiplication theorem of the gamma function and investigated the connection between the gamma function and elliptic integrals.
Karl Weierstrass further established the role of the gamma function in complex analysis, starting from yet another product representation,
where is Euler's constant. Weierstrass originally wrote his product as one for , in which case it is taken over the function's zeros rather than its poles. Inspired by this result, he proved what is known as the Weierstrass factorization theorem — that any entire function can be written as a product over its zeros in the complex plane; a generalization of the fundamental theorem of algebra.
The name gamma function and the symbol were introduced by Adrien-Marie Legendre around 1811; Legendre also rewrote Euler's integral definition in its modern form. Although the symbol is an upper-case Greek Gamma, there is no accepted standard for whether the function name should be written "Gamma function" or "gamma function" (some authors simply write "-function"). The alternative "Pi function" notation due to Gauss is sometimes encountered in older literature, but Legendre's notation is dominant in modern works.
It is justified to ask why we distinguish between the "ordinary factorial" and the gamma function by using distinct symbols, and particularly why the gamma function should be normalized to instead of simply using "". Legendre's motivation for the normalization does not appear to be known, and has been criticized as cumbersome by some (the 20th-century mathematician Cornelius Lanczos, for example, called it "void of any rationality" and would instead use [13]). The normalization does simplify some formulas, but complicates others.
19th-20th centuries: characterizing the gamma function
It is somewhat problematic that a large number of definitions have been given for the gamma function. Although they describe the same function, it is not entirely straightforward to prove the equivalence. Stirling never proved that his extended formula corresponds exactly to Euler's gamma function; a proof was first given by Charles Hermite in 1900.[14] Instead of finding a specialized proof for each formula, it would be desirable to have a general method of identifying the gamma function.
One way to prove would be to find a differential equation that characterizes the gamma function. Most special functions in applied mathematics arise as solutions to differential equations, whose solutions are unique. However, the gamma function does not appear to satisfy any simple differential equation. Otto Hölder proved in 1887 that the gamma function at least does not satisfy any algebraic differential equation by showing that a solution to such an equation could not satisfy the gamma function's recurrence formula. This result is known as Hölder's theorem.
A definite and generally applicable characterization of the gamma function was not given until 1922. Harald Bohr and Johannes Mollerup then proved what is known as the Bohr-Mollerup theorem: that the gamma function is the unique solution to the factorial recurrence relation that is positive and logarithmically convex for positive z and whose value at 1 is 1 (a function is logarithmically convex if its logarithm is convex).
The Bohr-Mollerup theorem is useful because it is relatively easy to prove logarithmic convexity for any of the different formulas used to define the gamma function. Taking things further, instead of defining the gamma function by any particular formula, we can choose the conditions of the Bohr-Mollerup theorem as the definition, and then pick any formula we like that satisfies the conditions as a starting point for studying the gamma function. This approach was used by the Bourbaki group.
Reference tables and software
Although the gamma function can be calculated virtually as easily as any mathematically simpler function with a modern computer — even with a programmable pocket calculator — this was of course not always the case. Until the mid-20th century, mathematicians relied on hand-made tables; in the case of the gamma function, notably a table computed by Gauss in 1813 and one computed by Legendre in 1825.
Tables of complex values of the gamma function, as well as hand-drawn graphs, were given in Tables of Higher Functions by Jahnke and Emde, first published in Germany in 1909. According to Michael Berry, "the publication in J&E of a three-dimensional graph showing the poles of the gamma function in the complex plane acquired an almost iconic status."[15]
There was in fact little practical need for anything but real values of the gamma function until the 1930s, when applications for the complex gamma function were discovered in theoretical physics. As electronic computers became available for the production of tables in the 1950s, several extensive tables for the complex gamma function were published to meet the demand, including a table accurate to 12 decimal places from the U.S. National Bureau of Standards.[10]
Like for many other special functions, Abramowitz and Stegun became the standard reference after its publication in 1964.
Double-precision floating-point implementations of the gamma function and its logarithm are now available in most scientific computing software and special functions libraries, for example Matlab, GNU Octave, and the GNU Scientific Library. The gamma function was also added to the C mathematics library (math.h) as part of the C99 standard, but is not implemented by all C compilers. Arbitrary-precision implementations are available in most computer algebra systems, such as Mathematica and Maple. Pari/GP, MPFR and MPFUN contain free arbitrary-precision implementations.
Notes and references
- ↑ Everywhere in this article, "log" denotes the natural logarithm.
- ↑ In the remainder of this article, "positive" will be understood to mean either a positive real number or a complex number with positive real part.
- ↑ Assuming that no poles are encountered
- ↑ Waldschmidt, M. (2006). "Transcendence of Periods: The State of the Art". Pure and Applied Mathematics Quarterly, Volume 2, Number 2, 435—463 (PDF copy published by the author)
- ↑ For instance, Abramowitz & Stegun, page 257
- ↑ Michon, G. P. "Trigonometry and Basic Functions". Numericana. Retrieved May 5, 2007.
- ↑ Chaudry, M. A. & Zubair, S. M. (2001). On A Class of Incomplete Gamma Functions with Applications. p. 37
- ↑ Rice, J. A. (1995). Mathematical Statistics and Data Analysis (Second Edition). p. 52–53
- ↑ Borwein, J., Bailey, D. H. & Girgensohn, R. (2003). Experimentation in Mathematics. A. K. Peters, 133. ISBN 1-56881-136-5.
- ↑ 10.0 10.1 Davis, P. J. (1959). "Leonhard Euler's Integral: A Historical Profile of the Gamma Function", The American Mathematical Monthly, Vol. 66, No. 10 (Dec., 1959), pp. 849-869
- ↑ Euler's paper was published in Commentarii academiae scientiarum Petropolitanae 5, 1738, 36—57. See E19 -- De progressionibus transcendentibus seu quarum termini generales algebraice dari nequeunt, from The Euler Archive, which includes a scanned copy of the original article. An English translation by S. Langton is also available.
- ↑ Remmert, R., Kay, L. D. (translator) (2006). Classical Topics in Complex Function Theory. Springer. ISBN 0387982213.
- ↑ Lanczos, C. (1964). "A precision approximation of the gamma function." J. SIAM Numer. Anal. Ser. B, Vol. 1.
- ↑ Knuth, D. E. (1997). The Art of Computer Programming, volume 1 (Fundamental Algorithms). Addison-Wesley.
- ↑ Berry, M. "Why are special functions special?". Physics Today, April 2001
















![{\displaystyle \Gamma (z+1)=\left[-e^{-t}t^{z}\right]_{0}^{\infty }+z\int _{0}^{\infty }e^{-t}t^{z-1}dt=z\Gamma (z).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9fa02312da3f296e53b4e84c5597ad4b6b8beb01)