Group (mathematics)/Catalogs: Difference between revisions
Jump to navigation
Jump to search

imported>Ragnar Schroder (→Examples of finite discrete groups: smaller pic, html coded text) |
imported>Peter Schmitt m (Examples of groups moved to Group (mathematics)/Catalogs: Let's move this to Group/Catalogs for the time beeing. Group and Group theory need cleaning up) |
||
| (9 intermediate revisions by 3 users not shown) | |||
| Line 13: | Line 13: | ||
===Examples of finite discrete groups=== | ===Examples of finite discrete groups=== | ||
*Let | # The trivial group consisting of just one element. | ||
*Let | # The group of order two, which f.i. can be represented by addition [[modular arithmetic|modulo]] 2 or the set {-1, 1} under multiplication. | ||
*Let | # The group of order three. | ||
# The [[cyclic group]] of order 4, which can be represented by addition [[modular arithmetic|modulo]] 4. | |||
# The noncyclic group of order 4, known as the "Klein [[viergruppe]]". A simple physical model of this group is two separate on-off switches. | |||
===Some physical models=== | |||
Some common physical objects provide excellent introductions to [[group theory]]. | |||
{|align="center" cellpadding="10" style="background-color:lightgray; width:75%; border: 1px solid #aaa; margin:2px; font-size: 90%;" | |||
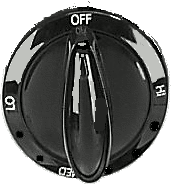
|'''Model of the [[cyclic group]] of order 4.''' | |||
{{Image|Examplesofgroups-Z4.gif|right|350px| Example of group Z4.}} | |||
*Let r<sub>1</sub> be the act of turning the knob 1 step clockwise. | |||
*Let r<sub>2</sub> be the act of turning the knob 2 steps clockwise. | |||
*Let r<sub>3</sub> be the act of turning the knob 3 steps clockwise. | |||
*Finally, let | *Finally, let r<sub>0</sub> be the act of just doing nothing. | ||
It's easy to see the following: | It's easy to see the following: | ||
*Doing | *Doing r<sub>1</sub> and then r<sub>1</sub> again gives the same result as doing r<sub>2</sub>. | ||
*Doing | *Doing r<sub>1</sub> and then r<sub>2</sub> gives the same result as doing r<sub>3</sub>. | ||
*Doing | *Doing r<sub>1</sub> and then r<sub>3</sub> gives the same result as doing nothing, i.e. r<sub>0</sub>. | ||
*... | |||
... | |||
These results can be summarized in the following table: | These results can be summarized in the following table: | ||
<table> | <table> | ||
<th>*</th> <th> | <th>*</th> <th>r<sub>0</sub></th> <th>r<sub>1</sub></th> <th>r<sub>2</sub></th> <th>r<sub>3</sub></th> | ||
<tr> | <tr> | ||
<td><b> | <td><b>r<sub>0</sub></b></td> <td>r<sub>0</sub></td> <td>r<sub>1</sub></td> <td>r<sub>2</sub></td> <td>r<sub>3</sub></td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td><b> | <td><b>r<sub>1</sub></b></td> <td>r<sub>1</sub></td> <td>r<sub>2</sub></td> <td>r<sub>3</sub></td> <td>r<sub>0</sub></td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td><b> | <td><b>r<sub>2</sub></b></td> <td>r<sub>2</sub></td> <td>r<sub>3</sub></td> <td>r<sub>0</sub></td> <td>r<sub>1</sub></td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td><b> | <td><b>r<sub>3</sub></b></td> <td>r<sub>3</sub></td> <td>r<sub>0</sub></td> <td>r<sub>1</sub></td> <td>r<sub>2</sub></td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
|} | |} | ||
{|align="center" cellpadding="10" style="background-color:lightgray; width:75%; border: 1px solid #aaa; margin:2px; font-size: 90%;" | |||
|'''Model of the non-cyclic group of order 4.''' | |||
[[Image:Examplesofgroups-Z2xZ2.gif|right|thumb|350px|{{#ifexist:Template:Examplesofgroups-Z4.gif/credit|{{Examplesofgroups-Z4.gif/credit}}<br/>|}} Example of group Z2 x Z2.]] | |||
*Let r<sub>01</sub> be the act of flipping the right button. | |||
*Let r<sub>10</sub> be the act of flipping the left button. | |||
*Let r<sub>11</sub> be the act of flipping both buttons. | |||
*Finally, let r<sub>00</sub> be the act of just doing nothing. | |||
It's easy to see the following: | |||
*Doing r<sub>01</sub> and then r<sub>01</sub> again gives the same result as doing r<sub>00</sub>, i.e. nothing. | |||
*Doing r<sub>01</sub> and then r<sub>10</sub> gives the same result as doing r<sub>11</sub>. | |||
*Doing r<sub>01</sub> and then r<sub>11</sub> gives the same result as doing r<sub>10</sub>. | |||
*... | |||
These results can be summarized in the following table: | |||
<table> | |||
<th>*</th> <th>r<sub>00</sub></th> <th>r<sub>01</sub></th> <th>r<sub>10</sub></th> <th>r<sub>11</sub></th> | |||
<tr> | |||
<td><b>r<sub>00</sub></b></td> <td>r<sub>00</sub></td> <td>r<sub>01</sub></td> <td>r<sub>10</sub></td> <td>r<sub>11</sub></td> | |||
</tr> | |||
<tr> | |||
<td><b>r<sub>01</sub></b></td> <td>r<sub>01</sub></td> <td>r<sub>00</sub></td> <td>r<sub>11</sub></td> <td>r<sub>10</sub></td> | |||
</tr> | |||
<tr> | |||
<td><b>r<sub>10</sub></b></td> <td>r<sub>10</sub></td> <td>r<sub>11</sub></td> <td>r<sub>00</sub></td> <td>r<sub>01</sub></td> | |||
</tr> | |||
<tr> | |||
<td><b>r<sub>11</sub></b></td> <td>r<sub>11</sub></td> <td>r<sub>10</sub></td> <td>r<sub>01</sub></td> <td>r<sub>00</sub></td> | |||
</tr> | |||
</table> | |||
|} | |||
Many | Many examples of groups come from considering some object and a set of [[bijective function]]s from the object to itself, which preserve some structure that this object has. | ||
* [[Topological groups]]: | * [[Topological groups]]: | ||
Latest revision as of 09:52, 15 September 2009
The mathematical group concept represents a rather simple and natural generalization of common phenomena, so examples of groups are easily found, from all areas of mathematics.
Different classes of groups
Three different classes of groups are commonly studied:
Examples of finite discrete groups
- The trivial group consisting of just one element.
- The group of order two, which f.i. can be represented by addition modulo 2 or the set {-1, 1} under multiplication.
- The group of order three.
- The cyclic group of order 4, which can be represented by addition modulo 4.
- The noncyclic group of order 4, known as the "Klein viergruppe". A simple physical model of this group is two separate on-off switches.
Some physical models
Some common physical objects provide excellent introductions to group theory.
Model of the cyclic group of order 4.
It's easy to see the following:
|
Model of the non-cyclic group of order 4.
It's easy to see the following:
These results can be summarized in the following table:
|
Many examples of groups come from considering some object and a set of bijective functions from the object to itself, which preserve some structure that this object has.