Polyhedron: Difference between revisions
imported>Anthony Argyriou (start archimedian solids) |
mNo edit summary |
||
| (3 intermediate revisions by 2 users not shown) | |||
| Line 13: | Line 13: | ||
</gallery> | </gallery> | ||
A convex polyhedron bounded by faces of more than one type of regular polygon, with all edges the same length and all vertices identical is called an [[ | A convex polyhedron bounded by faces of more than one type of regular polygon, with all edges the same length and all vertices identical is called an [[Archimedean solid]]. There are 13 Archimedean solids, shown below: | ||
<gallery> | <gallery> | ||
Image:TruncatedTetrahedron.png|[[truncated tetrahedron]]:4 hexagon + 4 triangle faces | Image:TruncatedTetrahedron.png|[[truncated tetrahedron]]:<br />4 hexagon + 4 triangle faces<br />12 vertices, 18 edges | ||
Image:TruncatedCube.png|[[truncated cube]]: 6 octagon + 8 triangle faces | Image:TruncatedCube.png|[[truncated cube]]:<br />6 octagon + 8 triangle faces<br />24 vertices, 36 edges | ||
Image:TruncatedOctahedron.png|[[truncated octahedron]]: 8 hexagon + 6 square faces | Image:TruncatedOctahedron.png|[[truncated octahedron]]:<br />8 hexagon + 6 square faces<br />24 vertices, 36 edges | ||
Image:TruncatedDodecahedron.png|[[truncated dodecahedron]]: 12 decagon + 20 triangular faces | Image:TruncatedDodecahedron.png|[[truncated dodecahedron]]:<br />12 decagon + 20 triangular faces<br />60 vertices, 90 edges | ||
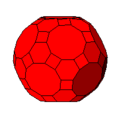
Image:TruncatedIcosahedron.png|[[truncated icosahedron]]: 20 hexagon + 12 pentagon faces, 60 vertices, | Image:TruncatedIcosahedron.png|[[truncated icosahedron]]:<br />20 hexagon + 12 pentagon faces<br />60 vertices, 90 edges | ||
</gallery> | Image:Cuboctahedron.png|[[cuboctahedron]]:<br />8 triangle + 6 square faces<br />12 vertices, 24 edges | ||
Image:Rhombicuboctahedron.png|[[rhombicuboctahedron]]:<br />18 square + 8 triangle faces<br />24 vertices, 48 edges | |||
Image:TruncatedCuboctahedron.png|[[truncated cuboctahedron]] (or '''great rhombicuboctahedron'''):<br />8 octagon + 8 hexagon + 12 square faces<br />48 vertices, 72 edges | |||
Image:Icosidodecahedron.png|[[icosidodecahedron]]:<br />20 triangle + 12 pentagon faces<br />30 vertices, 60 edges | |||
Image:Rhombicosidodecahedron.png|[[rhombicosidodecahedron]]:<br />20 triangle + 30 square + 12 pentagon faces<br />60 vertices, 120 edges | |||
Image:TruncatedIcosidodecahedron.png|[[truncated icosidodecahedron]] (or '''great rhombicosidodecahedron'''):<br />30 square + 20 hexagon + 12 decagon faces<br />120 vertices, 180 edges | |||
Image:SnubCube.png|[[snub cube]]:<br />32 triangle + 6 square faces<br />24 vertices, 60 edges | |||
Image:SnubDodecahedron.png|[[snub dodecahedron]]:<br />80 triangle + 12 pentagon faces<br />60 vertices, 150 edges | |||
</gallery>[[Category:Suggestion Bot Tag]] | |||
Latest revision as of 16:00, 5 October 2024
A polyhedron is a three-dimensional geometric closed figure bounded by a connected set of polygons. A polyhedron, in Euclidian geometry, must have at least four faces. A polyhedron of four sides is called a tetrahedron, six sides a hexahedron, eight sides an octahedron, ten sides a decahedron. Figures with more sides are typically named with the Greek name for the number of sides, followed by "-hedron".
The polygons bounding a polyhedron are known as faces; the line segments bounding the polygons are known as edges, and the points where the faces meet are vertices (singular vertex).
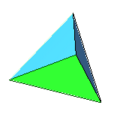
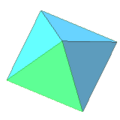
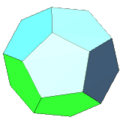
A convex polyhedron bounded by faces which are all the same-sized regular polygon is known as a Platonic solid. There are only five Platonic solids, shown below:
regular tetrahedron:4 triangle faces, 4 vertices, 6 edges
regular octahedron: 8 triangle faces, 6 vertices, 12 edges
regular dodecahedron: 12 pentagon faces, 20 vertices, 30 edges
regular icosahedron: 20 triangle faces, 12 vertices, 30 edges
A convex polyhedron bounded by faces of more than one type of regular polygon, with all edges the same length and all vertices identical is called an Archimedean solid. There are 13 Archimedean solids, shown below:
truncated tetrahedron:
4 hexagon + 4 triangle faces
12 vertices, 18 edgestruncated cube:
6 octagon + 8 triangle faces
24 vertices, 36 edgestruncated octahedron:
8 hexagon + 6 square faces
24 vertices, 36 edgestruncated dodecahedron:
12 decagon + 20 triangular faces
60 vertices, 90 edgestruncated icosahedron:
20 hexagon + 12 pentagon faces
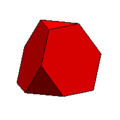
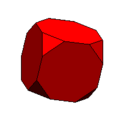
60 vertices, 90 edgescuboctahedron:
8 triangle + 6 square faces
12 vertices, 24 edgesrhombicuboctahedron:
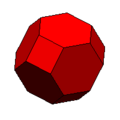
18 square + 8 triangle faces
24 vertices, 48 edgestruncated cuboctahedron (or great rhombicuboctahedron):
8 octagon + 8 hexagon + 12 square faces
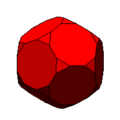
48 vertices, 72 edgesicosidodecahedron:
20 triangle + 12 pentagon faces
30 vertices, 60 edgesrhombicosidodecahedron:
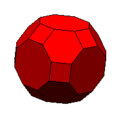
20 triangle + 30 square + 12 pentagon faces
60 vertices, 120 edgestruncated icosidodecahedron (or great rhombicosidodecahedron):
30 square + 20 hexagon + 12 decagon faces
120 vertices, 180 edgessnub cube:
32 triangle + 6 square faces
24 vertices, 60 edgessnub dodecahedron:
80 triangle + 12 pentagon faces
60 vertices, 150 edges