Triple product: Difference between revisions
imported>Paul Wormer (New page: {{subpages}} right|thumb|350px|Parallelepiped spanned by vectors '''A''', '''B''', and '''C''' (shown in red). In analytic geometry, a '''triple product'''...) |
mNo edit summary |
||
| (4 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{subpages}} | {{subpages}} | ||
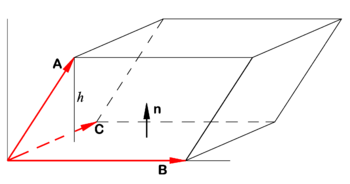
{{Image|Triple product.png|right|350px|Parallelepiped spanned by vectors '''A''', '''B''', and '''C''' (shown in red).}} | |||
In [[analytic geometry]], a '''triple product''' is a common term for a product of three vectors '''A''', '''B''', and '''C''' leading to a scalar (a number). The absolute value of this scalar is the volume ''V'' of the parallelepiped spanned by the three vectors: | In [[analytic geometry]], a '''triple product''' is a common term for a product of three vectors '''A''', '''B''', and '''C''' leading to a [[scalar]] (a number). The absolute value of this scalar is the volume ''V'' of the parallelepiped spanned by the three vectors: | ||
:<math> | :<math> | ||
V = \big|\mathbf{A}\cdot(\mathbf{B}\times\mathbf{C})\big|, | V = \big|\mathbf{A}\cdot(\mathbf{B}\times\mathbf{C})\big|, | ||
</math> | </math> | ||
where '''B''' × '''C''' is the [[cross product]] of two vectors (resulting into a vector) and the dot indicates the [[inner product]] between two vectors (a scalar). | where '''B''' × '''C''' is the [[cross product]] of two vectors (resulting into a vector) and the dot indicates the [[inner product]] between two vectors (a scalar). | ||
The triple product is sometimes called the ''scalar triple product'' to distinguish it from the ''vector triple product'' '''A'''×('''B'''×'''C'''). The scalar triple product is often written as ['''A''' '''B''' '''C''']. The vector triple product can be expanded by the aid of the [[baccab formula]]. | |||
==Explanation== | ==Explanation== | ||
Let '''n''' be a unit normal to the parallelogram spanned by '''B''' and '''C''' (see figure). Let ''h'' be the height of the terminal point of the vector '''A''' above the base of the parallelepiped. Recall: | Let '''n''' be a unit normal to the parallelogram spanned by '''B''' and '''C''' (see figure). Let ''h'' be the height of the terminal point of the vector '''A''' above the base of the parallelepiped. Recall: | ||
| Line 65: | Line 68: | ||
==Reference== | ==Reference== | ||
M. R. Spiegel, ''Theory and Problems of Vector Analysis'', Schaum Publishing, New York (1959) p. 26 | M. R. Spiegel, ''Theory and Problems of Vector Analysis'', Schaum Publishing, New York (1959) p. 26 | ||
[[Category:Suggestion Bot Tag]] | |||
Latest revision as of 16:00, 30 October 2024
In analytic geometry, a triple product is a common term for a product of three vectors A, B, and C leading to a scalar (a number). The absolute value of this scalar is the volume V of the parallelepiped spanned by the three vectors:
where B × C is the cross product of two vectors (resulting into a vector) and the dot indicates the inner product between two vectors (a scalar).
The triple product is sometimes called the scalar triple product to distinguish it from the vector triple product A×(B×C). The scalar triple product is often written as [A B C]. The vector triple product can be expanded by the aid of the baccab formula.
Explanation
Let n be a unit normal to the parallelogram spanned by B and C (see figure). Let h be the height of the terminal point of the vector A above the base of the parallelepiped. Recall:
- Volume V of parallelepiped is height h times area S of the base.
Note that h is the projection of A on n and that the area S is the length of the cross product of the vectors spanning the base,
Use
where it is used that
(The unit normal n has the direction of the cross product B × C).
If A, B, and C do not form a right-handed system, A•n < 0 and we must take the absolute value: | A• (B×C)|.
Triple product as determinant
Take three orthogonal unit vectors i , j, and k and write
The triple product is equal to a 3 × 3 determinant
Indeed, writing the cross product as a determinant we find
Since a determinant is invariant under cyclic permutation of its rows, it follows
Reference
M. R. Spiegel, Theory and Problems of Vector Analysis, Schaum Publishing, New York (1959) p. 26






![{\displaystyle {\begin{aligned}\mathbf {A} \cdot (\mathbf {B} \times \mathbf {C} )&=\mathbf {A} \cdot {\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\B_{1}&B_{2}&B_{3}\\C_{1}&C_{2}&C_{3}\\\end{vmatrix}}\\&={\big (}A_{1}\mathbf {i} +A_{2}\mathbf {j} +A_{3}\mathbf {k} {\big )}\cdot {\big [}(B_{2}\,C_{3}-B_{3}\,C_{2})\;\mathbf {i} +(B_{3}\,C_{1}-B_{1}\,C_{3})\;\mathbf {j} +(B_{1}\,C_{2}-B_{2}\,C_{1})\;\mathbf {k} {\big ]}\\&=A_{1}\;(B_{2}\,C_{3}-B_{3}\,C_{2})+A_{2}\;(B_{3}\,C_{1}-B_{1}\,C_{3})+A_{3}\;(B_{1}\,C_{2}-B_{2}\,C_{1})\\&={\begin{vmatrix}A_{1}&A_{2}&A_{3}\\B_{1}&B_{2}&B_{3}\\C_{1}&C_{2}&C_{3}\\\end{vmatrix}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59d7af0616ddf13297024357fc90e030e39b4534)
