imported>Paul Wormer |
imported>Paul Wormer |
| (55 intermediate revisions by the same user not shown) |
| Line 1: |
Line 1: |
| ==Rotations in <math>\mathbb{R}^3</math> == | | ==Parabolic mirror== |
| Consider a real 3×3 matrix '''R''' with columns
| | {{Image|Refl parab.png|right|350px|Fig. 2. Reflection in a parabolic mirror}} |
| '''r'''<sub>1</sub>, '''r'''<sub>2</sub>, '''r'''<sub>3</sub>,
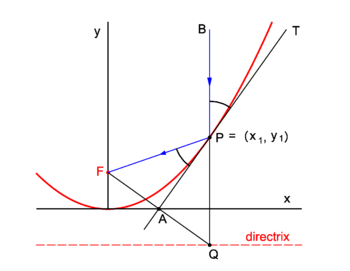
| | Parabolic mirrors concentrate incoming vertical light beams in their focus. We show this. |
| i.e.,
| |
| :<math>
| |
| \mathbf{R} = \left(\mathbf{r}_1,\, \mathbf{r}_2,\, \mathbf{r}_3 \right)
| |
| </math>.
| |
| The matrix '''R''' is ''orthogonal'' if
| |
| :<math>
| |
| \mathbf{r}_i \cdot \mathbf{r}_j = \delta_{ij}, \quad i,j = 1,2,3 .
| |
| </math>
| |
| The matrix '''R''' is a ''proper rotation matrix'', if it is
| |
| orthogonal ''and'' if '''r'''<sub>1</sub>, '''r'''<sub>2</sub>,
| |
| '''r'''<sub>3</sub> form a right-handed set, i.e.,
| |
| :<math>
| |
| \mathbf{r}_i \times \mathbf{r}_j = \sum_{k=1}^3 \, \varepsilon_{ijk}
| |
| \mathbf{r}_k .
| |
| </math>
| |
| Here the symbol × indicates a
| |
| [[cross product]] and <math>\varepsilon_{ijk}</math> is the
| |
| antisymmetric [[Levi-Civita symbol]],
| |
| :<math>
| |
| \begin{align}
| |
| \varepsilon_{123} =&\; \varepsilon_{312} = \varepsilon_{231} = 1 \\
| |
| \varepsilon_{213} =&\; \varepsilon_{321} = \varepsilon_{132} = -1
| |
| \end{align}
| |
| </math>
| |
| and <math>\varepsilon_{ijk} = 0</math> if two or more indices are equal.
| |
|
| |
|
| The matrix '''R''' is an ''improper rotation matrix'' if
| | Consider in figure 2 the arbitrary vertical light beam (blue, parallel to the ''y''-axis) that enters the parabola and hits it at point ''P'' = (''x''<sub>1</sub>, ''y''<sub>1</sub>). The parabola (red) has focus in point ''F''. The incoming beam is reflected at ''P'' obeying the well-known law: incidence angle is angle of reflection. The angles involved are with the line ''APT'' which is tangent to the parabola at point ''P''. It will be shown that the reflected beam passes through ''F''. |
| its column vectors form a left-handed set, i.e.,
| |
| :<math>
| |
| \mathbf{r}_i \times \mathbf{r}_j = - \sum_{k=1}^3 \, \varepsilon_{ijk}
| |
| \mathbf{r}_k \; .
| |
| </math>
| |
| The last two equations can be condensed into one equation
| |
| :<math>
| |
| \mathbf{r}_i \times \mathbf{r}_j = \det(\mathbf{R}) \sum_{k=1}^3 \;
| |
| \varepsilon_{ijk} \mathbf{r}_k
| |
| </math>
| |
| by virtue of the the fact that
| |
| the determinant of a proper rotation matrix is 1 and of an improper | |
| rotation −1. This can be proved as follows:
| |
| The determinant of a 3×3 matrix with column vectors '''a''',
| |
| '''b''', and '''c''' can be written as [[scalar triple product#Triple product as determinant|scalar triple product]]
| |
| :<math>
| |
| \det\left(\mathbf{a},\,\mathbf{b},\, \mathbf{c}\right) =
| |
| \mathbf{a} \cdot (\mathbf{b}\times\mathbf{c})
| |
| </math>. | |
| Remember that for a proper rotation
| |
| the columns of '''R''' are orthonormal and satisfy,
| |
| :<math> | |
| \mathbf{r}_1 \cdot (\mathbf{r}_2 \times \mathbf{r}_3 ) = \sum_k \,
| |
| \varepsilon_{23k} \,
| |
| \mathbf{r}_1 \cdot \mathbf{r}_k = \varepsilon_{231} = 1 .
| |
| </math>
| |
| Likewise the determinant is −1 for an improper rotation.
| |
| | |
| ====Theorem====
| |
| A proper rotation matrix '''R''' can be
| |
| factorized thus
| |
| :<math>
| |
| \mathbf{R} = \mathbf{R}_z (\omega_3 ) \; \mathbf{R}_y (\omega_2 ) \; \mathbf{R}_x (\omega_1 )
| |
| </math>
| |
| which is referred to as the ''Euler z-y-x parametrization'', | |
| or also as
| |
| :<math>
| |
| \mathbf{R} = \mathbf{R}_z (\alpha) \; \mathbf{R}_y (\beta ) \; \mathbf{R}_z (\gamma ) \quad
| |
| </math>
| |
| the ''Euler z-y-z parametrization''. | |
|
| |
|
| Here the matrices representing rotations around the ''z'', ''y'', and ''x'' axis, respectively, over arbitrary angle φ, are
| | Clearly ∠''BPT'' = ∠''QPA'' (they are vertically opposite angles). Further ∠''APQ'' = ∠''FPA'' because the triangles ''FPA'' and ''QPA'' are congruent and hence ∠''FPA'' = ∠''BPT''. |
| :<math>
| |
| \mathbf{R}_z (\varphi ) \equiv
| |
| \begin{pmatrix}
| |
| \cos \varphi & -\sin \varphi & 0 \\
| |
| \sin \varphi & \cos \varphi & 0 \\
| |
| 0 & 0 & 1 \\
| |
| \end{pmatrix}, \quad
| |
| \mathbf{R}_y (\varphi ) \equiv
| |
| \begin{pmatrix}
| |
| \cos \varphi & 0 & \sin \varphi \\
| |
| 0 & 1 & 0 \\
| |
| -\sin \varphi& 0 & \cos \varphi \\
| |
| \end{pmatrix}, \quad
| |
| \mathbf{R}_x (\varphi ) \equiv
| |
| \begin{pmatrix}
| |
| 1 & 0 & 0 \\
| |
| 0 & \cos \varphi & -\sin \varphi \\
| |
| 0 & \sin \varphi & \cos \varphi \\
| |
| \end{pmatrix} .
| |
| </math>
| |
| ====Proof====
| |
| First the Euler ''z-y-x''-parametrization will be proved by describing an
| |
| algorithm for the factorization of '''R'''.
| |
| Consider to that end the matrix product
| |
| :<math>
| |
| \mathbf{R}_z (\omega_3 ) \, \mathbf{R}_y (\omega_2 ) =
| |
| \begin{pmatrix}
| |
| \cos \omega_3 \cos \omega_2 & -\sin \omega_3 & \cos \omega_3 \sin \omega_2 \\
| |
| \sin \omega_3 \cos \omega_2 & \cos \omega_3 & \sin \omega_3 \sin \omega_2 \\
| |
| -\sin \omega_2 & 0 & \cos \omega_2 \\
| |
| \end{pmatrix} \equiv
| |
| (\mathbf{a}_1 , \mathbf{a}_2 , \mathbf{a}_3 ) .
| |
| </math>
| |
| The columns of the matrix product are for ease of reference designated by '''a'''<sub>1</sub>, '''a'''<sub>2</sub>, and '''a'''<sub>3</sub>.
| |
| Note that the multiplication by
| |
| '''R'''<sub>''x''</sub>(ω<sub>1</sub>) on the right
| |
| does not affect the first column, so that '''a'''<sub>1</sub> =
| |
| '''r'''<sub>1</sub> (the first column of the matrix to be factorized).
| |
| Solve <math>\omega_2\;</math> and <math>\omega_3\;</math> from the first column of
| |
| '''R''',
| |
| :<math>
| |
| \mathbf{a}_1 =
| |
| \begin{pmatrix}
| |
| \cos \omega_3 \; \cos \omega_2 \\
| |
| \sin \omega_3 \; \cos \omega_2 \\
| |
| -\sin \omega_2 \\
| |
| \end{pmatrix} =
| |
| \begin{pmatrix}
| |
| R_{11} \\
| |
| R_{21} \\
| |
| R_{31} \\
| |
| \end{pmatrix} \equiv \mathbf{r}_1 .
| |
| </math>
| |
| This is possible. First solve <math>\omega_2\;</math> for <math> -\pi/2 \leq \omega_2
| |
| \leq \pi/2</math> from
| |
| :<math>
| |
| \sin \omega_2 = - R_{31}. \,
| |
| </math>
| |
| Then solve <math>\omega_3\;</math> for <math>0 \leq \omega_3 \leq 2 \pi</math> from the two equations:
| |
| :<math>
| |
| \begin{align}
| |
| \cos \omega_3 =& {R_{11} \over \cos \omega_2} \\
| |
| \sin \omega_3 =& {R_{21} \over \cos \omega_2} .
| |
| \end{align}
| |
| </math>
| |
| Knowledge of <math>\omega_2\;</math> and <math>\omega_3\;</math> determines the vectors '''a'''<sub>2</sub> and '''a'''<sub>3</sub>.
| |
|
| |
|
| Since '''a'''<sub>1</sub>, '''a'''<sub>2</sub> and '''a'''<sub>3</sub> are the columns of a
| | We prove the congruence of the triangles: By the definition of the parabola the line segments ''FP'' and ''QP'' are of equal length, because the length of the latter segment is the distance of ''P'' to the directrix and the length of ''FP'' is the distance of ''P'' to the focus. The point ''F'' has the coordinates (0,''f'') and the point ''Q'' has the coordinates (''x''<sub>1</sub>, −''f''). The line segment ''FQ'' has the equation |
| proper rotation matrix they form an orthonormal right-handed system. The plane spanned by '''a'''<sub>2</sub> and '''a'''<sub>3</sub> is orthogonal to <math> \mathbf{a}_1 \equiv \mathbf{r}_1</math> and hence the plane contains <math>\mathbf{r}_2</math> and
| |
| <math>\mathbf{r}_3</math>. Thus the latter two vectors are a linear combination of the first two,
| |
| :<math>
| |
| ( \mathbf{r}_2 , \mathbf{r}_3 ) = (\mathbf{a}_2 , \mathbf{a}_3 )
| |
| \begin{pmatrix}
| |
| \cos \omega_1 & -\sin \omega_1 \\
| |
| \sin \omega_1 & \cos \omega_1 \\
| |
| \end{pmatrix} .
| |
| </math>
| |
| Since <math>\mathbf{r}_2,\; \mathbf{a}_2,\; \mathbf{a}_3</math> are
| |
| known unit vectors we can compute
| |
| :<math> | | :<math> |
| \begin{align} | | \lambda\begin{pmatrix}0\\ f\end{pmatrix} + (1-\lambda)\begin{pmatrix}x_1\\ -f\end{pmatrix}, \quad 0\le\lambda\le 1. |
| \mathbf{a}_2 \cdot \mathbf{r}_2 =& \cos \omega_1 \\ | |
| \mathbf{a}_3 \cdot \mathbf{r}_2 =& \sin \omega_1.
| |
| \end{align}
| |
| </math> | | </math> |
| These equations give <math>\omega_1\;</math> with <math> 0 \leq \omega_1 \leq 2 \pi</math>.
| | The midpoint ''A'' of ''FQ'' has coordinates (λ = ½): |
| | |
| Augment the 2×2 matrix to the 3×3 matrix <math>\mathbf{R}_x(\omega_1)</math>, then
| |
| :<math> | | :<math> |
| \begin{align} | | \frac{1}{2}\begin{pmatrix}0\\ f\end{pmatrix} + \frac{1}{2}\begin{pmatrix}x_1\\ -f\end{pmatrix} = |
| \mathbf{R} \equiv ( \mathbf{r}_1 , \mathbf{r}_2 , \mathbf{r}_3 ) = (
| | \begin{pmatrix}\frac{1}{2} x_1\\ 0\end{pmatrix}. |
| \mathbf{r}_1 , \mathbf{a}_2 , \mathbf{a}_3 ) | |
| \mathbf{R}_x (\omega_1 ) | |
| = (\mathbf{a}_1, \mathbf{a}_2, \mathbf{a}_3)\mathbf{R}_x (\omega_1 )
| |
| = \mathbf{R}_z (\omega_3 ) \, \mathbf{R}_y (\omega_2 ) \, \mathbf{R}_x (\omega_1 ) .
| |
| \end{align}
| |
| </math> | | </math> |
| This concludes the proof of the ''z-y-x'' parametrization.
| | Hence ''A'' lies on the ''x''-axis. |
| | | The parabola has equation, |
| The Euler ''z-y-z'' parametrization is obtained by a small modification of the previous proof. Solve
| |
| <math>\omega_2\;</math> and
| |
| <math>\omega_3\;</math> from <math>\mathbf{r}_3 = \mathbf{a}_3 </math> (the rightmost multiplication by '''R'''<sub>''z''</sub>(ω<sub>1</sub>) does not affect '''r'''<sub>3</sub>)
| |
| and then consider
| |
| :<math> | | :<math> |
| ( \mathbf{r}_1, \; \mathbf{r}_2 ) = (\mathbf{a}_1, \; \mathbf{a}_2 )
| | y = \frac{1}{4f} x^2. |
| \begin{pmatrix}
| |
| \cos \omega_1 & -\sin \omega_1 \\
| |
| \sin \omega_1 & \cos \omega_1 \\
| |
| \end{pmatrix}
| |
| </math>
| |
| or,
| |
| <math>
| |
| \mathbf{a}_1 \cdot \mathbf{r}_1 = \cos \omega_1 \; , \quad \mathbf{a}_2 \cdot
| |
| \mathbf{r}_1 = \sin
| |
| \omega_1 .
| |
| </math> | | </math> |
| The equation for '''R''' can be written as | | The equation of the tangent at ''P'' is |
| :<math> | | :<math> |
| ( \mathbf{r}_1 , \mathbf{r}_2 , \mathbf{r}_3 ) =
| | y = y_1 + \frac{x_1}{2f} (x-x_1)\quad \hbox{with}\quad y_1 = \frac{x_1^2}{4f}. |
| ( \mathbf{a}_1 , \mathbf{a}_2 , \mathbf{r}_3 ) \, \mathbf{R}_z (\omega_1 ) = \mathbf{R}_z (\omega_3 ) \, | |
| \mathbf{R}_y (\omega_2 ) \, \mathbf{R}_z (\omega_1 ) \; ,
| |
| </math> | | </math> |
| which proves the Euler ''z-y-z'' parametrization. It is common in this parametrization to write
| | This line intersects the ''x''-axis at ''y'' = 0, |
| :<math> | | :<math> |
| \omega_3 = \alpha,\quad \omega_2 = \beta, \quad \omega_1 = \gamma. | | 0 = \frac{x_1^2}{4f} - \frac{x_1^2}{2f} + \frac{x_1}{2f} x |
| | \Longrightarrow \frac{x_1}{2f} x = \frac{x_1^2}{4f} \longrightarrow x = \tfrac{1}{2}x_1. |
| </math> | | </math> |
| | The intersection of the tangent with the ''x''-axis is the point ''A'' = (½''x''<sub>1</sub>, 0) that lies on the midpoint of ''FQ''. The corresponding sides of the triangles ''FPA'' and ''QPA'' are of equal length and hence the triangles are congruent. |