imported>John R. Brews |
|
| (2 intermediate revisions by one other user not shown) |
| Line 1: |
Line 1: |
| | {{AccountNotLive}} |
| ==Forces== | | ==Forces== |
| {{Gallery-mixed | | {{Gallery-mixed |
| Line 39: |
Line 40: |
| |width=200 | | |width=200 |
| |lines=5 | | |lines=5 |
| | |Polar coordinates.png|Polar coordinates (''R'', θ). |
| |Changing coordinates.png|Locating a particle in two coordinate systems, S and S'. | | |Changing coordinates.png|Locating a particle in two coordinate systems, S and S'. |
| |Uniform circular motion.png|Changing velocity direction in circular motion at constant speed implies a radially inward acceleration. | | |Uniform circular motion.png|Changing velocity direction in circular motion at constant speed implies a radially inward acceleration. |
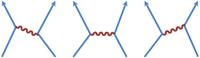
| | |Photon exchange.png|Photon exchange between two electrons.''Left'': electron (arrow) on left absorbs photon (squiggle); ''Center'': simultaneous emission and absorption; ''Right'': electron on left emits photon. |
| }} | | }} |
|
| |
|
Latest revision as of 03:07, 22 November 2023
The account of this former contributor was not re-activated after the server upgrade of March 2022.
Forces
| Forces
|
|
|
(CC) Image: John R. Brews
|
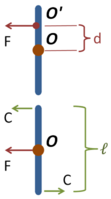
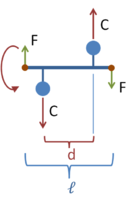
Force and its equivalent force and couple
|
|
|
(PD) Image: John R. Brews
|
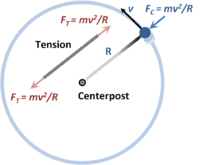
Centripetal force FC upon an object held in circular motion by a string of length R. The string is under tension FT, as shown separately to the left.
|
|
|
(PD) Image: John R. Brews
|
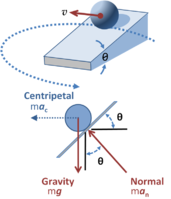
Upper panel: Ball on a banked circular track moving with constant speed v; Lower panel: Forces on the ball.
|
|
|
(PD) Image: John R. Brews
|
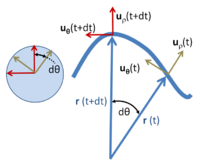
Polar unit vectors at two times t and t + dt for a particle with trajectory r ( t ); on the left the unit vectors uρ and uθ at the two times are moved so their tails all meet, and are shown to trace an arc of a unit radius circle.
|
|
|
(PD) Image: John R. Brews
|
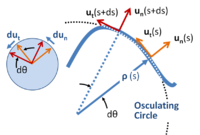
Local coordinate system for planar motion on a curve.
|
|
|
(PD) Image: John R. Brews
|
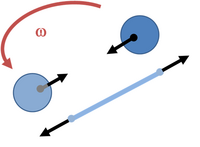
Exploded view of rotating spheres in an inertial frame of reference showing the centripetal forces on the spheres provided by the tension in a rope tying them together.
|
|
|
(PD) Image: John R. Brews
|
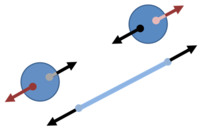
Rotating spheres subject to centrifugal (outward) force in a co-rotating frame in addition to the (inward) tension from the rope.
|
|
|
(PD) Image: John R. Brews
|
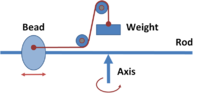
The "whirling table". The rod is made to rotate about the axis and (from the bead's viewpoint) the centrifugal force acting on the sliding bead is balanced by the weight attached by a cord over two pulleys.
|
|
|
(PD) Image: John R. Brews
|
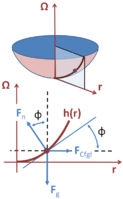
Force diagram for an element of water surface in co-rotating frame.
|
|
|
(PD) Image: John R. Brews
|
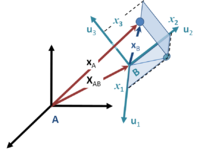
An object located at xA in inertial frame A is located at location xB in accelerating frame B.
|
|
|
(PD) Image: John R. Brews
|
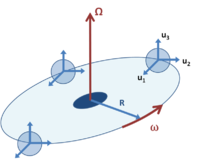
An orbiting but fixed orientation coordinate system B, shown at three different times.
|
|
|
(PD) Image: John R. Brews
|
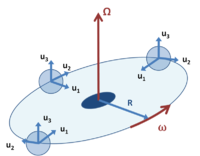
An orbiting coordinate system B in which unit vectors uj, j = 1, 2, 3 rotate to face the rotational axis.
|
|
|
|
|
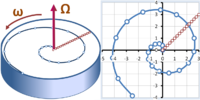
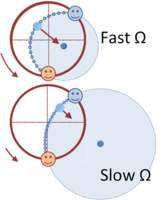
Crossing a rotating carousel walking at constant speed, a spiral is traced out in the inertial frame, while a simple straight radial path is seen in the frame of the carousel.
|
|
|
(PD) Image: John R. Brews
|
Rotating shaft unbalanced by two identical attached weights.
Image
|
|
|
(PD) Image: John R. Brews
|
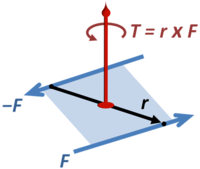
Torque vector T representing a force couple.
|
|
|
(PD) Image: John R. Brews
|
An ellipsoid showing its axes
|
|
|
(PD) Image: John R. Brews
|
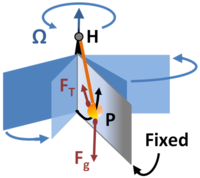
While the pendulum P swings in a fixed plane about its hanger at H, the planes of the Earth observer rotate.
|
|
|
(PD) Image: John R. Brews
|
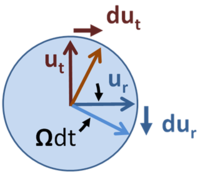
As time progresses each unit vector's change is orthogonal to it.
|
|
|
(PD) Image: John R. Brews
|
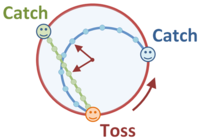
Tossed ball on carousel. At the center of the carousel, the path is a straight line for a stationary observer, and is an arc for a rotating observer.
|
|
|
(PD) Image: John R. Brews
|
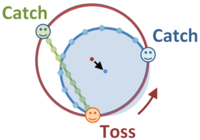
From the center of curvature of the path, the ball executes approximate circular motion.
|
|
|
(PD) Image: John R. Brews
|
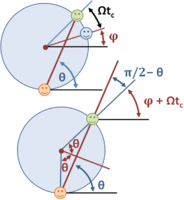
Some useful notation for the ball toss on a carousel.
|
|
|
(PD) Image: John R. Brews
|
The ball follows a nearly circular path about the center of curvature.
|
|
|
(PD) Image: John R. Brews
|
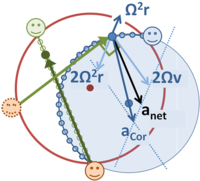
The inertial forces on the ball combine to provide the resultant centripetal force required by Newton's laws for circular motion.
|
|
|
(PD) Image: John R. Brews
|
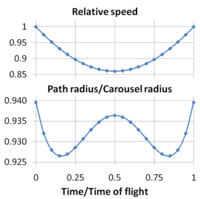
Stats for a particular path of ball toss.
|
|
|
(PD) Image: John R. Brews
|
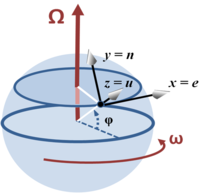
Tangent-plane coordinate system on rotating Earth at latitude φ.
|
|
|
(PD) Image: John R. Brews
|
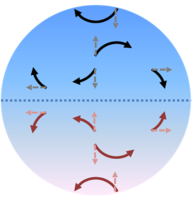
Wind motion in direction of pressure gradient is deflected by the Coriolis force.
|
|
|
(PD) Image: John R. Brews
|
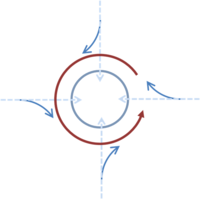
In the northern hemisphere, Coriolis force forms a counterclockwise flow.
|
|
|
(PD) Image: John R. Brews
|
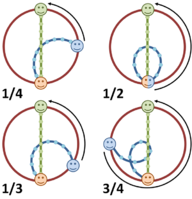
Path of ball for four rates of rotation. Catcher positioned so the catch is made at 12 o'clock in all cases.
|
|
|
(PD) Image: John R. Brews
|
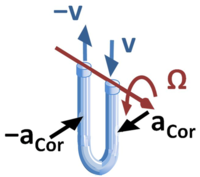
A fluid forced through a rocking tube experiences a Coriolis acceleration.
|
|
| Forces
|
|
|
(PD) Image: John R. Brews
|
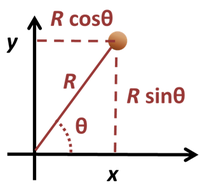
Polar coordinates (R, θ).
|
|
|
(PD) Image: John R. Brews
|
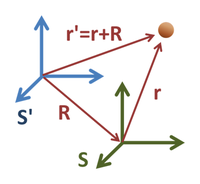
Locating a particle in two coordinate systems, S and S'.
|
|
|
(PD) Image: John R. Brews
|
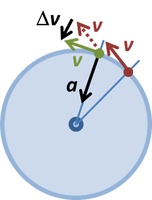
Changing velocity direction in circular motion at constant speed implies a radially inward acceleration.
|
|
|
(PD) Image: John R. Brews
|
Photon exchange between two electrons.Left: electron (arrow) on left absorbs photon (squiggle); Center: simultaneous emission and absorption; Right: electron on left emits photon.
|
|
Particles
| Particles
|
|
|
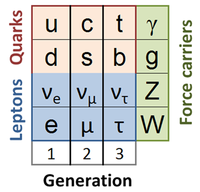
(PD) Image: John R. Brews
|
The fundamental particles and messenger quanta of the Standard Model.
|
|
|
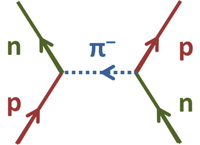
(PD) Image: John R. Brews
|
A neutron and proton trade identities by exchange of a π− in the Yukawa model.
|
|