Fast Fourier transform: Difference between revisions
imported>Dmitrii Kouznetsov (edit "confusion" Some dollars still should be treted) |
imported>Pat Palmer (adding subpages and categories) |
||
| (10 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
The ''' | {{subpages}} | ||
The '''fast Fourier transform''' or '''FFT''', is the efficient algorithm for the numerical evaluation of the [[Discrete Fouler transform]] defined with | |||
: <math>\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\displaystyle (1) ~ ~ ~ | : <math>\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\displaystyle (1) ~ ~ ~ | ||
B_k=\sum_{m=0}^{N-1} A_m \exp\Big(-\mathrm{i} \frac{2 \pi}{N}~ k~ m\Big)</math> | B_k=\sum_{m=0}^{N-1} A_m \exp\Big(-\mathrm{i} \frac{2 \pi}{N}~ k~ m\Big)</math> | ||
where <math>N</math> is natural number; usually, <math>2^q</math> for some natural <math>q</math>;<br> | where <math>N</math> is natural number; usually, <math>N=2^q</math> for some natural <math>q</math>;<br> | ||
<math>A</math> is the input array of length <math>N</math>, numbered beginning from 0;<br> | |||
<math>B</math> is the output array of length <math>N</math>, numbered beginning from 0.<br> | |||
<math>k</math> is also integer number, <math>0\le k < N</math>. | |||
There are many ways of evaluation of the expression (1). | There are many ways of evaluation of the expression (1). | ||
The trivial one would requires of order of | The trivial one would requires of order of <math>N^2</math> operations. | ||
The efficient way requires of order on | The efficient way requires of order on <math>N~ \log_2 N</math> operations and called '''FFT'''. | ||
<ref | At large <math>N</math>, the time of evaluation by the direct implementation is many orders of magnitude larger than that with FFT; therefore, FFT is often used for the harmonic analysis, expansion by modes, calculation of the | ||
http:// | [[Fourier coefficient]]s or approximation of the [[Fourier operator]]. | ||
</ref> | There are several efficient algorithms to perform the FFT.<ref>{{cite web|title=Fast Fourier Transform (FFT)|url=http://www.mathworks.com/help/matlab/math/fast-fourier-transform-fft.html|publisher=The MathWorks|accessdate=22 October 2013}}</ref> | ||
One of the simplest algorithms realized in the implementation of the | One of the simplest algorithms realized in the implementation of the | ||
| Line 19: | Line 20: | ||
fafo(*complex(double), int, int) of the [[Fourier operator]]. | fafo(*complex(double), int, int) of the [[Fourier operator]]. | ||
More advanced algorithms allow the | More advanced algorithms allow the efficient evaluation even if <math>N</math> is not an integer power of 2, although for the fast evaluation <math>N</math> should not have large [[prime number|prime factor]]s. | ||
==Common confusion== | ==Common confusion== | ||
The often confusion about FFT is the believe that FFT somehow implements, or approximates the [[Fourier operator]]. | The often confusion about FFT is the believe that FFT somehow implements, or approximates the [[Fourier operator]]. | ||
| Line 32: | Line 32: | ||
==FFT and fafo== | ==FFT and fafo== | ||
The routine "fafo" is used in calculations described in articles | The routine "fafo" is used in calculations of field in lasers, described in articles | ||
<ref name="voit"> | <ref name="voit"> | ||
http://tori.ils.uec.ac.jp/PAPERS/1997density.pdf | http://tori.ils.uec.ac.jp/PAPERS/1997density.pdf | ||
| Line 50: | Line 50: | ||
http://tori.ils.uec.ac.jp/PAPERS/PhysRevA_72_013617.pdf | http://tori.ils.uec.ac.jp/PAPERS/PhysRevA_72_013617.pdf | ||
D.Kouznetsov, H.Oberst. Scattering of waves at ridged mirrors. [[Phys.Rev.A]], v.72, 013617 (2005) | D.Kouznetsov, H.Oberst. Scattering of waves at ridged mirrors. [[Phys.Rev.A]], v.72, 013617 (2005) | ||
</ref> and for plotting of some pictures in [[TORI]]. | </ref> and for plotting of some pictures in [[TORI]]. Before the similar method is used by E.A.Sziklas and A.E.Siegman | ||
<ref> | |||
http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=1451368 | |||
Sziklas, E.A., Siegman, A.E. Diffraction calculations using fast Fourier transform methods. | |||
Proceedings of the IEEE, 1974, Volume: 62 , Issue: 3, Page(s): 410 - 412. | |||
</ref><ref> | |||
http://www.opticsinfobase.org/ao/abstract.cfm?id=19537 | |||
Mode calculations in unstable resonators with flowing saturable gain. 2: Fast Fourier transform method. Applied Optics, Vol. 14, Issue 8, pp. 1874-1889 (1975) http://dx.doi.org/10.1364/AO.14.001874 | |||
</ref> and other researchers. Application of Fourier methods in optics is discussed also in the book by Okan Ersov | |||
<ref> | |||
http://as.wiley.com/WileyCDA/WileyTitle/productCd-0471238163.html | |||
Okan Ersov. Diffraction, Fourier Optics and Imaging. November 2006. ISBN: 978-0-471-23816-4, 413 pages. | |||
(preview: http://books.google.co.jp/books?hl=en&lr=&id=hpyUlD4OEdsC&oi=fnd&pg=PR13&dq=Diffraction+Fourier&ots=zpLQJ-h22q&sig=ABVuQc-kgnrXg0FpGE4fg7uhVtw&redir_esc=y#v=onepage&q=Diffraction%20Fourier&f=false ) | |||
</ref>. | |||
Since year 2011, [[fafo.cin]] is available with examples. This routine | Since year 2011, [[fafo.cin]] is available with examples. This routine takes less than one screen of code, and it seems to be compatible with various operational systems, the only [[C++]] is required. The reason of use of the fafo.cin is not the performance (perhaps some factor of order of 0.5 can be achieved at the optimization of the [[CPU time]]), but its compactness, readability and portability; no any "installing" is necessary after the downloading. | ||
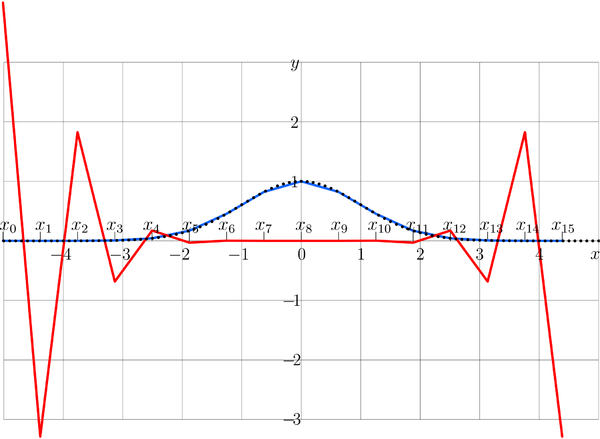
[[File:FFTexample16T.png|600px|right|thumb| Comparison of the self–Fourier Gaussian exponential (dotted curve) to its discrete representation | [[File:FFTexample16T.png|600px|right|thumb| Comparison of the self–Fourier Gaussian exponential (dotted curve) to its discrete representation <math>A</math> by (2), blue line (and it coincides with its [[Fourier transform]]), and its FFT by (1), red line]] | ||
The operator defined with (1) is often confused with the implementation of the [[Fourier operator]]; | The operator defined with (1) is often confused with the implementation of the [[Fourier operator]]; | ||
both replace the input array to the output one. But the result is not the same. | both replace the input array to the output one. But the result is not the same. | ||
The simplest way to see the difference is to perform the transform of the array of values of the Gaussian exponential, let | The simplest way to see the difference is to perform the transform of the array of values of the Gaussian exponential, let | ||
: | : <math> \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\displaystyle (2) ~ ~ ~ A_k=\exp(- x_k^2/2~ )</math> | ||
: | : <math> \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\displaystyle (3) ~ ~ ~ x_k= (k-N/2) d</math> | ||
where | where | ||
It is assumed that | <math>d=\sqrt{2 \pi/N}</math> is step of the equidistant grid. | ||
It is assumed that <math>k</math> is integer; <math>0\!\le\!k\!<\!N</math>. | |||
The expression (2) defines the discrete analogy of the simplest [[self-Fourier]] function. With such an input array, | The expression (2) defines the discrete analogy of the simplest [[self-Fourier]] function. With such an input array, | ||
The fafo returns almost the same array as that at the input (at least, beginning with | The fafo returns almost the same array as that at the input (at least, beginning with <math>N=8</math>); | ||
the FFT returns some set of values that are difficult to interpret in terms of the Fourier operator. | the FFT returns some set of values that are difficult to interpret in terms of the Fourier operator. | ||
The case of the Gaussian self-Fourier function by (2) is shown at the figure at right for | The case of the Gaussian self-Fourier function by (2) is shown at the figure at right for <math>N\!=\!16</math>.<br> | ||
The dotted curve shows | The dotted curve shows <math>y=\exp(-x^2/2)</math>; this is initial exponential.<br> | ||
The blue segmented line shows its discrete representation by (2). This representation practically coincide with the numerical estimate for its Fourier transform<br> | The blue segmented line shows its discrete representation by (2). This representation practically coincide with the numerical estimate for its Fourier transform by routine fafo.<br> | ||
The Red curve shows the Discrete Fourier Transform, that is equivalent to equation (1). | The Red curve shows the Discrete Fourier Transform, that is equivalent to equation (1). | ||
If for the Gaussian exponential, the routine fft returns the array similar to that shown at the figure with red line, then this indicates that, perhaps, the routine works correctly and returns the approximation for the sum by | If for the Gaussian exponential, the routine fft returns the array similar to that shown at the figure with red line, then this indicates that, perhaps, the routine works correctly and returns the approximation for the sum by equation (1). | ||
The fft is used for the implementation of fafo; and it can be easy extracted from there. | The fft is used for the implementation of fafo; and it can be easy extracted from there. | ||
| Line 87: | Line 101: | ||
The way of realization of these functions may be dependent of the matlab version; | The way of realization of these functions may be dependent of the matlab version; | ||
one can play with these functions and experimentally find the way of calling, that approximates the [[Fourier operator]] | one can play with these functions and experimentally find the way of calling, that approximates the [[Fourier operator]] | ||
: | : <math>\!\!\!\!\!\!\!\!\!\!\!\!\! (4) ~ ~ ~ \displaystyle \mathrm{Fourier}(A)(x)= \frac{1}{\sqrt{2\pi}} \int_{- \infty}^{\infty} \exp( - \mathrm{i} x y) A(y) ~ \mathrm{d} y </math> | ||
==Keywords== | ==Keywords== | ||
[[Fourier operator]], [[Fourier transform]] | [[Fourier operator]], [[Fourier transform]] | ||
==References== | ==References== | ||
{{reflist}} | |||
The content of this article is adopted from http://tori.ils.uec.ac.jp/TORI/index.php/FFT | |||
Latest revision as of 10:59, 8 September 2020
The fast Fourier transform or FFT, is the efficient algorithm for the numerical evaluation of the Discrete Fouler transform defined with
where is natural number; usually, for some natural ;
is the input array of length , numbered beginning from 0;
is the output array of length , numbered beginning from 0.
is also integer number, .
There are many ways of evaluation of the expression (1). The trivial one would requires of order of operations. The efficient way requires of order on operations and called FFT. At large , the time of evaluation by the direct implementation is many orders of magnitude larger than that with FFT; therefore, FFT is often used for the harmonic analysis, expansion by modes, calculation of the Fourier coefficients or approximation of the Fourier operator. There are several efficient algorithms to perform the FFT.[1]
One of the simplest algorithms realized in the implementation of the C++ routine fft(*complex(double), int, int) is stored in file fafo.cin. This routine is used in the implementation fafo(*complex(double), int, int) of the Fourier operator.
More advanced algorithms allow the efficient evaluation even if is not an integer power of 2, although for the fast evaluation should not have large prime factors.
Common confusion
The often confusion about FFT is the believe that FFT somehow implements, or approximates the Fourier operator.
Unfortunately, this believe is just wrong. Actually, FFT does not approximate the Fourier operator at all.
However FFT can be used to make the numerical implementation of the Fourier operator. One of such implementations is loaded as fafo.cin.
The difference between FFT and the numerical implementation of the Fourier operator is discussed in the next section.
FFT and fafo
The routine "fafo" is used in calculations of field in lasers, described in articles [2][3][4][5][6][7] and for plotting of some pictures in TORI. Before the similar method is used by E.A.Sziklas and A.E.Siegman [8][9] and other researchers. Application of Fourier methods in optics is discussed also in the book by Okan Ersov [10].
Since year 2011, fafo.cin is available with examples. This routine takes less than one screen of code, and it seems to be compatible with various operational systems, the only C++ is required. The reason of use of the fafo.cin is not the performance (perhaps some factor of order of 0.5 can be achieved at the optimization of the CPU time), but its compactness, readability and portability; no any "installing" is necessary after the downloading.
The operator defined with (1) is often confused with the implementation of the Fourier operator; both replace the input array to the output one. But the result is not the same. The simplest way to see the difference is to perform the transform of the array of values of the Gaussian exponential, let
where is step of the equidistant grid. It is assumed that is integer; . The expression (2) defines the discrete analogy of the simplest self-Fourier function. With such an input array, The fafo returns almost the same array as that at the input (at least, beginning with ); the FFT returns some set of values that are difficult to interpret in terms of the Fourier operator.
The case of the Gaussian self-Fourier function by (2) is shown at the figure at right for .
The dotted curve shows ; this is initial exponential.
The blue segmented line shows its discrete representation by (2). This representation practically coincide with the numerical estimate for its Fourier transform by routine fafo.
The Red curve shows the Discrete Fourier Transform, that is equivalent to equation (1).
If for the Gaussian exponential, the routine fft returns the array similar to that shown at the figure with red line, then this indicates that, perhaps, the routine works correctly and returns the approximation for the sum by equation (1).
The fft is used for the implementation of fafo; and it can be easy extracted from there. The algorithm of expression of fafo through the FFT is realized through the displacement of the elements of array. This can be done by various ways; the most straightforward (as simplest to understand) is realized.
Matlab and other languages
For the translation of fafo to other languages (for example, Matlab), where FFT is already implemented, there is no need to translate FFT routine. In particular, the conventional Matlabs's fft can be used "as is".
The numeric implementation of the fafo through the matlab built-in function fft can be even simplified using the built-in functions "fftshift" and "ifftshift"; For the array X, the correct call may have form [11]
- ifftshift(fftshift(X))
The way of realization of these functions may be dependent of the matlab version; one can play with these functions and experimentally find the way of calling, that approximates the Fourier operator
Keywords
Fourier operator, Fourier transform
References
- ↑ Fast Fourier Transform (FFT). The MathWorks. Retrieved on 22 October 2013.
- ↑ http://tori.ils.uec.ac.jp/PAPERS/1997density.pdf V.V.Voitsekhovich, D.Kouznetsov, D.Kh.Morozov. Density of turbulence-induced phase dislocations. Applied Optics, 1998, v.37, No.21, p.4525-4535.
- ↑ http://tori.ils.uec.ac.jp/PAPERS/josa1f0.pdf D.Kouznetsov, J.V.Moloney, E.M.Wright. Efficiency of pump in the double-clad fiber amplifiers. 1. Fiber with circular symmetry. JOSA B, June 2001, V.18, No.6, p.743-749.
- ↑ http://tori.ils.uec.ac.jp/PAPERS/josa2f0.pdf D.Kouznetsov, J.V.Moloney. Efficiency of pump in the double-clad fiber amplifiers. 2. Broken circular symmetry. JOSA B, V.19, No.6, p.1259-1263 (2002).
- ↑ D.Kouznetsov, J.V.Moloney. Efficiency of pump absorption in double-clad fibers amplifiers. 3. Calculation of modes. JOSA B, V.19, No.6, p.1304-1309 (2002).
- ↑ http://tori.ils.uec.ac.jp/PAPERS/ieee3.pdf P.Kano, D.Kouznetsov, J.V.Moloney, M.Brio. Slab delivery of incoherent pump light to double-clad fiber amplifiers: Numerical simulations. IEEE Journal of Quantum Electronics, 2004, v.40, No.9, p.1301-1305.
- ↑ http://tori.ils.uec.ac.jp/PAPERS/PhysRevA_72_013617.pdf D.Kouznetsov, H.Oberst. Scattering of waves at ridged mirrors. Phys.Rev.A, v.72, 013617 (2005)
- ↑ http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=1451368 Sziklas, E.A., Siegman, A.E. Diffraction calculations using fast Fourier transform methods. Proceedings of the IEEE, 1974, Volume: 62 , Issue: 3, Page(s): 410 - 412.
- ↑ http://www.opticsinfobase.org/ao/abstract.cfm?id=19537 Mode calculations in unstable resonators with flowing saturable gain. 2: Fast Fourier transform method. Applied Optics, Vol. 14, Issue 8, pp. 1874-1889 (1975) http://dx.doi.org/10.1364/AO.14.001874
- ↑ http://as.wiley.com/WileyCDA/WileyTitle/productCd-0471238163.html Okan Ersov. Diffraction, Fourier Optics and Imaging. November 2006. ISBN: 978-0-471-23816-4, 413 pages. (preview: http://books.google.co.jp/books?hl=en&lr=&id=hpyUlD4OEdsC&oi=fnd&pg=PR13&dq=Diffraction+Fourier&ots=zpLQJ-h22q&sig=ABVuQc-kgnrXg0FpGE4fg7uhVtw&redir_esc=y#v=onepage&q=Diffraction%20Fourier&f=false )
- ↑ http://www.mathworks.co.jp/help/techdoc/ref/fftshift.html
The content of this article is adopted from http://tori.ils.uec.ac.jp/TORI/index.php/FFT

















