Pythagorean theorem: Difference between revisions
Jump to navigation
Jump to search
imported>Michael Hardy (illustration added) |
imported>Michael Hardy (expanded on the statement) |
||
| Line 1: | Line 1: | ||
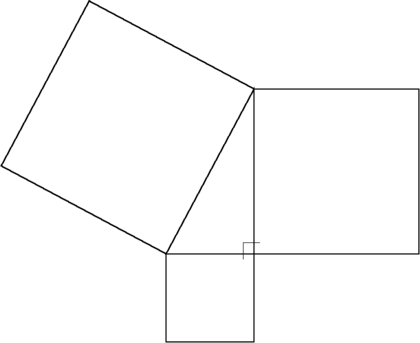
[[Image:Pythagorean.png|thumb|420px|'''The Pythagorean theorem''': The sum of the areas of the two squares on the legs (the sides that meet at a [[right angle]]) equals the area of the square on the hypotenuse (the side opposite the right angle).]] | [[Image:Pythagorean.png|thumb|420px|'''The Pythagorean theorem''': The sum of the areas of the two squares on the legs (the sides that meet at a [[right angle]]) equals the area of the square on the hypotenuse (the side opposite the right angle).]] | ||
In [[Euclidean geometry]], the '''Pythagorean theorem''' states that | In [[Euclidean geometry]], the '''Pythagorean theorem''' states that: | ||
:: The sum of the areas of the squares on the legs of a [[right triangle]] equals the area of the square on the [[hypotenuse]]. | |||
The "legs" are the two sides of the triangle that meet at a right angle. The hypotenuse is the other side—the side opposite the right angle. | |||
{{stub}} | {{stub}} | ||
Revision as of 21:07, 15 May 2007

The Pythagorean theorem: The sum of the areas of the two squares on the legs (the sides that meet at a right angle) equals the area of the square on the hypotenuse (the side opposite the right angle).
In Euclidean geometry, the Pythagorean theorem states that:
- The sum of the areas of the squares on the legs of a right triangle equals the area of the square on the hypotenuse.
The "legs" are the two sides of the triangle that meet at a right angle. The hypotenuse is the other side—the side opposite the right angle.