Angular momentum (classical): Difference between revisions
imported>Paul Wormer No edit summary |
imported>Paul Wormer |
||
| Line 40: | Line 40: | ||
The former case occurs when the mass moves uniformly in homogeneous space (no external forces). Then also the linear momentum of the point mass is conserved, and therefore one rarely considers the angular momentum in the case of uniform rectilinear motion. | The former case occurs when the mass moves uniformly in homogeneous space (no external forces). Then also the linear momentum of the point mass is conserved, and therefore one rarely considers the angular momentum in the case of uniform rectilinear motion. | ||
The second case is more interesting. Let us assume that '''F''' is [[conservative (physics)|conservative]], i.e., its [[curl]] vanishes, then '''F''' is the gradient of a potential ''V''(''x'',''y'',''z''), | The second case is more interesting. Let us assume that '''F''' is [[conservative (physics)|conservative]], i.e., its [[curl]] vanishes, then '''F''' is the [[gradient]] '''∇''' of a potential ''V''(''x'',''y'',''z''), | ||
:<math> | :<math> | ||
\mathbf{\nabla}\times \mathbf{F} = 0 \Longrightarrow \mathbf{F} = - \mathbf{\nabla} V(x,y,z), | \mathbf{\nabla}\times \mathbf{F} = 0 \Longrightarrow \mathbf{F} = - \mathbf{\nabla} V(x,y,z), | ||
| Line 63: | Line 63: | ||
A well-known example is the motion of the earth around the sun. To a very good approximation the [[gravitation]] is central-symmetric (rotationally invariant) and hence the earth's orbit is characterized by a conserved angular momentum. [[Kepler's laws|Kepler's]] second law is a direct consequence of this conservation of angular momentum. | A well-known example is the motion of the earth around the sun. To a very good approximation the [[gravitation]] is central-symmetric (rotationally invariant) and hence the earth's orbit is characterized by a conserved angular momentum. [[Kepler's laws|Kepler's]] second law is a direct consequence of this conservation of angular momentum. | ||
===Generalization to ''n'' point masses=== | |||
When the particles do ''not'' interact mutually, the generalization to ''n'' particles is simply | |||
:<math> | |||
\mathbf{\dot{L}}_i = \mathbf{r}_i \times \mathbf{F}_i \Longrightarrow | |||
\mathbf{\dot{L}}_\mathrm{sys} = \sum_{i=1}^n \mathbf{r}_i \times \mathbf{F}_i, | |||
</math> | |||
where the forces are external. If the sum on the right hand side is zero, i.e., the total external torque is zero, the total angular momentum of the system is conserved. | |||
When the particles do interact, i.e., internal forces exist, then the result still holds, provided the internal forces are central-symmetric and additive. No internal torque occurs in that case. In order to show this, we recall that Newton's first law (action = −reaction) holds for central-symmetric forces, | |||
:<math> | |||
\mathbf{F}_{ij} = - \mathbf{F}_{ji}, \qquad i \ne j. | |||
</math> | |||
where the left hand side is the force on particle ''i'' executed by particle ''j'' and the right hand side is '' i'' acting on '' j''. Both forces act along the vector pointing form particle ''i'' to ''j'', | |||
:<math> | |||
\mathbf{r}_{ij} = \mathbf{r}_j - \mathbf{r}_i, | |||
</math> | |||
so that | |||
:<math> | |||
\mathbf{r}_{ij}\times \mathbf{F}_{ij} = (\mathbf{r}_j - \mathbf{r}_i)\times \mathbf{F}_{ij} = | |||
-(\mathbf{r}_j \times \mathbf{F}_{ji} + \mathbf{r}_i\times \mathbf{F}_{ij}) = 0 | |||
</math> | |||
Under assumption of a pair-wise additive force, the total internal torque can be written as | |||
:<math> | |||
\mathbf{N}^\mathrm{int}_\mathrm{sys} = \sum_{i=1}^n \sum^n_{{j=1\atop j\ne i}} \mathbf{r}_{ij}\times \mathbf{F}_{ij} = - \sum_{i=1}^n \sum^n_{j>i} | |||
(\mathbf{r}_{i}\times \mathbf{F}_{ij} + \mathbf{r}_{j}\times \mathbf{F}_{ji}) = 0, | |||
</math> | |||
and | |||
:<math> | |||
\mathbf{\dot{L}}_i = \mathbf{N}^\mathrm{ext}_\mathrm{sys} = \sum_{i=1}^n \mathbf{r}_i \times \mathbf{F}_i, | |||
</math> | |||
where '''F'''<sub>'' i''</sub> is external. | |||
==Separation of center of mass== | ==Separation of center of mass== | ||
Revision as of 04:21, 19 December 2007
In physics, angular momentum is a kinematic property of a system consisting of one or more point masses. Its importance derives from the fact that it is conserved in several physical circumstances. (Recall that a conserved property of a system is one that does not change over time.)
Definition
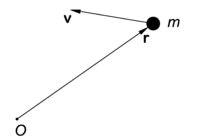
The angular momentum of a single point mass m is defined with respect to a point O. Denote the vector from O to m by r (see the figure). Let the mass have velocity v, then the angular momentum L of the point mass is defined as the cross product,
It follows from the definition of cross product that the vector L is perpendicular to the plane of the figure and points towards the reader. Note that the definition p ≡ m v for the linear momentum is introduced here.
The definition of the angular momentum of a system of n point masses is the following simple generalization:
Conservation of angular momentum
For simplicity we consider the case of one point mass, generalization to n point masses is straightforward. The following important result will be proved: a particle that moves in a centrally symmetric potential has a conserved angular momentum.
Using Newton's dot (fluxion) notation for time derivatives, we find
Use
where we invoked Newton's second law Hence the time derivative of the angular momentum is equal to the torque N,
It follows that the angular momentum is conserved—i.e., its time derivative is zero—if the applied torque N is zero, which means that either F is zero, or r and F are parallel, because in that case the cross product vanishes.
The former case occurs when the mass moves uniformly in homogeneous space (no external forces). Then also the linear momentum of the point mass is conserved, and therefore one rarely considers the angular momentum in the case of uniform rectilinear motion.
The second case is more interesting. Let us assume that F is conservative, i.e., its curl vanishes, then F is the gradient ∇ of a potential V(x,y,z),
so that for a conservative force the time derivative of L is
The quantity in brackets is known in group theory as a Lie derivative of the full rotation group SO(3). In quantum mechanics it is a well-known operator, namely the orbital angular momentum operator (except for the factor ).
From the general properties of Lie derivatives—or equivalently orbital angular momenta—it follows that the time derivative of L vanishes whenever the potential V(x,y,z) is rotationally invariant (isotropic, central-symmetric). This means that the function V(x,y,z) depends on r only, when expressed in spherical polar coordinates (r, θ, φ). By expressing the gradient ∇ in spherical polar coordinates and writing the cross product as a determinant, we can prove this explicitly, using that the derivatives of V with respect to θ and φ are zero,
A well-known example is the motion of the earth around the sun. To a very good approximation the gravitation is central-symmetric (rotationally invariant) and hence the earth's orbit is characterized by a conserved angular momentum. Kepler's second law is a direct consequence of this conservation of angular momentum.
Generalization to n point masses
When the particles do not interact mutually, the generalization to n particles is simply
where the forces are external. If the sum on the right hand side is zero, i.e., the total external torque is zero, the total angular momentum of the system is conserved.
When the particles do interact, i.e., internal forces exist, then the result still holds, provided the internal forces are central-symmetric and additive. No internal torque occurs in that case. In order to show this, we recall that Newton's first law (action = −reaction) holds for central-symmetric forces,
where the left hand side is the force on particle i executed by particle j and the right hand side is i acting on j. Both forces act along the vector pointing form particle i to j,
so that
Under assumption of a pair-wise additive force, the total internal torque can be written as
and
where F i is external.
Separation of center of mass
The angular momentum of a system of point masses with respect to an arbitrary point O can be separated into two terms. The first term is the angular momentum with respect to O of a particle with total mass M positioned at the center of mass C of the system. The other term is the sum of the angular momenta of the particles with respect to C.
The center of mass C is determined by
Introduce s i for particle i at point P i
Note that
and hence also
Now,
where the two cross terms vanished and the two diagonal terms are non-vanishing. The two remaining terms are:
If the total system moves in homogeneous (field free) space, the first term is conserved and is usually not of much interest. The second term, the sum of the angular momenta of the n particles with respect to the center of mass, is usually designated the total angular momentum of the system,
where the position vectors s i are defined with respect to a system of axes with origin in the center of mass C of the system.
Circular motion around a fixed axis
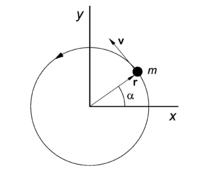
A system often encountered in physics is a particle (point mass) that moves along a circle in a fixed plane. Let us choose a system of axes such that the plane of motion is the x-y plane, with the z-axis perpendicular to the plane.
The coordinates of the particle and its time derivative are
where we used that the radius r of the circle is time-independent. The angular momentum is given by
The quantity mr 2 is the inertia moment I of the present simple system (particle on a circle) and ω is the angular velocity. The angular velocity, as defined here, is a scalar. Often the product ωez is defined as angular velocity ω, which is a vector.
In summary, for a particle moving on a circle around a fixed axis, the angular momentum is proportional to the angular velocity with the inertia moment as proportionality factor,
It is of some interest to point out that this simple relation becomes a vector-tensor relation for more general motions of more general systems (rigid rotors) for which the rotational axis is not fixed in space: L and ω remain vectors, but the inertia moment generalizes to a second rank, symmetric, tensor.