Equation (mathematics): Difference between revisions
imported>Daniel Mietchen m (Equation moved to Equation (mathematics): dambig) |
imported>Richard Pinch (expanded introduction and tidied up some spelling and syntax) |
||
| Line 1: | Line 1: | ||
{{subpages}} | {{subpages}} | ||
''' | In [[mathematics]], an '''equation''' is a relationship between quantities which are stated to be equal. It is usually regarded as a kind of mathematical problem in which at least one side of this equality is dependent on some [[variable]] (or variables); it is required to find the ''solution'', namely the value or set of values of these variables for which the equality holds '''[[true(mathematics)|true]]'''. For example, <math>x+2 = 3</math> is an equation in which the ''solution'' is the value <math>x=1</math>. | ||
An '''identity''' is an equality which is stated to be universally true for all permissible values of the variables, rather than representing a condition on those values. For example, <math>x+y = y+x</math> is an identity for real numbers, since it is true for all real values of ''x'' and ''y''. | |||
F(x)=0 | |||
</math> | The equation may have the form | ||
:(1) <math>F(x)=0</math> | |||
or | or | ||
:(2) <math>F(x)=G(x)</math> | |||
where <math> F </math> and <math>G</math> are [[known function]]s and <math>x</math> is [[unknown variable]] | where <math> F </math> and <math>G</math> are [[known function]]s and <math>x</math> is the [[unknown variable]]. | ||
An equation may have as solution somevalue of variable (<math>x </math> in the example above, although variable can be denoted by any letter, including letters from exotic alphabets), at which the equality has value '''true'''. | |||
It is usually supposed that the variable belongs to some set <math>\mathrm A</math>; for example, it may be specified that <math>x</math> is [[real(mathematics)|real]]. | |||
The equation may have no solution, may have one solution and may have many solutions, | The equation may have no solution, may have one solution and may have many solutions, depending on the form of the equations and the set <math>\mathrm A</math> of possible values. | ||
Equations are common in language used in [[science]]; especially in [[mathematics]] and [[physics]]: | Equations are common in the language used in [[science]]; especially in [[mathematics]] and [[physics]]: | ||
[[Newton equation]], equation of [[oscillator]], [[Schrödinger equation ]]. | [[Newton equation]], equation of [[oscillator]], [[Schrödinger equation ]]. | ||
The | The term '''equation''' is used also in [[chemistry]], indicating conservation of atomic or [[isotopic content|isotopic]] content at the [[chemical reaction]]s. | ||
==Examples== | ==Examples== | ||
| Line 35: | Line 35: | ||
<math>F_b(x)</math>, <math>G_b(x)</math>. | <math>F_b(x)</math>, <math>G_b(x)</math>. | ||
In relatively simple | In relatively simple cases, function <math> F </math> depends only on the unknown variable, and <math>G</math> | ||
depends on the parameter; for example, | depends on the parameter; for example, | ||
(3) <math>F(x)=b</math> . | (3) <math>F(x)=b</math> . | ||
In this case, the solution <math>x</math> is considered as [[inverse function]] of <math>b</math>, which can be written as | In this case, the solution <math>x</math> is considered as an [[inverse function]] of <math>b</math>, which can be written as | ||
(4) <math> x=F^{-1}(b)</math>. | (4) <math> x=F^{-1}(b)</math>. | ||
Dependending on the function <math>F</math>, range of values of <math>b</math> and set <math>\mathbf A</math>, there may exist no inverse function, | |||
one inverse function or several inverse functions. | one inverse function or several inverse functions. | ||
| Line 68: | Line 68: | ||
==[[Differential equation]]s and [[integral equation]]s== | ==[[Differential equation]]s and [[integral equation]]s== | ||
In particular, | In particular, the variable may denote a function of one or several variables, so that the set of p[ossible values is some [[Hilbert space]]; the function <math> F </math> is then an [[operator]] on this space which may be expressed in terms of derivatives or integrals of the function elements. | ||
function <math> F </math> may be expressed in terms of derivatives or integrals of | In these cases, the equation is called a [[differential equation]] or an [[integral equation]]. | ||
In these cases, the equation is called [[differential equation]] | |||
==[[Operator equation]]s== | ==[[Operator equation]]s== | ||
Equations can be used for objects of any | Equations can be used for objects of any origin, as soon, as the operation of [[equality]] is defined. In particular, in [[Quantum mechanics]], the [[Heisenberg equation]] deals with non-[[commutativity|commuting]] objects ([[operator(quantum mechanics)|operator]]s). | ||
[[Heisenberg equation]] deals with non-commuting objects ([[operator(quantum mechanics)|operator]]s). | |||
Revision as of 12:35, 21 November 2008
In mathematics, an equation is a relationship between quantities which are stated to be equal. It is usually regarded as a kind of mathematical problem in which at least one side of this equality is dependent on some variable (or variables); it is required to find the solution, namely the value or set of values of these variables for which the equality holds true. For example, is an equation in which the solution is the value .
An identity is an equality which is stated to be universally true for all permissible values of the variables, rather than representing a condition on those values. For example, is an identity for real numbers, since it is true for all real values of x and y.
The equation may have the form
- (1)
or
- (2)
where and are known functions and is the unknown variable.
An equation may have as solution somevalue of variable ( in the example above, although variable can be denoted by any letter, including letters from exotic alphabets), at which the equality has value true. It is usually supposed that the variable belongs to some set ; for example, it may be specified that is real.
The equation may have no solution, may have one solution and may have many solutions, depending on the form of the equations and the set of possible values.
Equations are common in the language used in science; especially in mathematics and physics: Newton equation, equation of oscillator, Schrödinger equation . The term equation is used also in chemistry, indicating conservation of atomic or isotopic content at the chemical reactions.
Examples
For function , the equation (1) has no solutions among natural numbers, but has solution in the set of integer numbers.
Equation has no solutions among rational numbers, has one solution () among positive real numbers, and has two soluitons ( and ) among real numbers.
Inverse function
Function in equation (1) ; or functions and in equation (2) may also depend on some parameter(s). In this case, the solution(s) also may depend on parameter(s). Indicating the function, the parameter, say, , can be specified as a second argument, writing , or as subscript, writing , .
In relatively simple cases, function depends only on the unknown variable, and depends on the parameter; for example,
(3) .
In this case, the solution is considered as an inverse function of , which can be written as
(4) .
Dependending on the function , range of values of and set , there may exist no inverse function, one inverse function or several inverse functions.
Graphical solution of equations
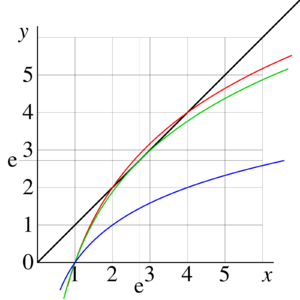
Solving equations, it may worth to begin with graphic solution of the equation, which allows the quick and dirty estimates. One plots both functions, and at the same graphic, and watch the point (s) of the intersection of the curves. In figire 1, functions is plotted with black line, and function is plotted with red curve. The intersections with black curve indicate values of which are solutions.
At the same figure, the cases (only one solution, ) and (no solutions among real numbers) are shown with green and blue curves.
System of equations
In the equations (1) or (2), may denote several numbers at once, ; and functions and may return values from multidimentional space . In this case, one says that there is system of equations. For example, there is well developed theory of systems of linear equations, while unknown variables are real or complex numbers.
Differential equations and integral equations
In particular, the variable may denote a function of one or several variables, so that the set of p[ossible values is some Hilbert space; the function is then an operator on this space which may be expressed in terms of derivatives or integrals of the function elements. In these cases, the equation is called a differential equation or an integral equation.
Operator equations
Equations can be used for objects of any origin, as soon, as the operation of equality is defined. In particular, in Quantum mechanics, the Heisenberg equation deals with non-commuting objects (operators).