Legendre-Gauss Quadrature formula: Difference between revisions
imported>Dmitrii Kouznetsov |
imported>Dmitrii Kouznetsov (Did not finish yet.) |
||
| Line 1: | Line 1: | ||
{{Copyedit}} | {{Copyedit}} | ||
'''Legendre-Gauss Quadratude formiula''' is the approximation of the integral | '''Legendre-Gauss Quadratude formiula''' is the approximation of the integral | ||
:(1) <math>\int_{-1}^1 f(x)\,dx \approx \sum_{i=1}^N w_i f(x_i).</math> | :(1) <math>\int_{-1}^1 f(x)\,dx \approx \sum_{i=1}^N w_i f(x_i).</math> | ||
Revision as of 08:11, 27 May 2008
Legendre-Gauss Quadratude formiula is the approximation of the integral
- (1)
with special choice of nodes and weights , characterised in that, if the finction is polynomial of order smallet than , then the exact equality takes place in equation (1).
Legendre-Gauss quadratude formula is special case of Gaussian quadratures of more general kind, which allow efficient approximation of a function with known asumptiotic behavior at the edges of the interval of integration.
Nodes and weights
Nodes in equation (1) are zeros of the Polunomial of Lehendre :
- (2)
- (3)
Weight in equaiton (1) can be expressed with
- (4)
There is no straightforward espression for the nodes ; they can be approximated with many decimal digits through only few iterations, solving numerically equation (2) with initial approach
- (5)
These formulas are described in the books [1] [2]
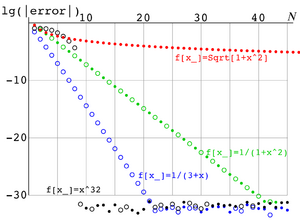
Precision of the approximation
Example
Extension to other interval
is straightforward. Should I copypast the obvious formulas here?
References
- ↑ (1980) Handbook on special functions.
- ↑ Numerical Resipes in C. Do not forget to type data of the ref. here!.