Fuzzy subset: Difference between revisions
imported>Giangiacomo Gerla |
imported>Giangiacomo Gerla |
||
| Line 8: | Line 8: | ||
=== The notion of fuzzy subset === | === The notion of fuzzy subset === | ||
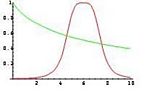
{{Image|Fuzzy1.JPG|right| | {{Image|Fuzzy1.JPG|right|150px|the fuzzy subset of small number and the fuzzy subset of numbers close to 6.}} | ||
An attempt to give an answer to such a question was proposed in 1965 by Lotfi Zadeh and at the same time, by Dieter Klaua in the framework of multi-valued logic. Now recall that the ''[[characteristic function]]'' of a classical subset ''X'' of ''S'' is the map ''c''<sub>X</sub> : → {0,1} such that ''c<sub>X</sub>''(''x'') = 1 if ''x'' is an element in ''X'' and ''c<sub>X</sub>''(''x'') = 0 otherwise. Obviously, it is possible to identify every subset ''X'' with its characteristic function ''c<sub>X</sub>'' and therefore the extension of a property with a suitable characteristic function. This suggests that we can define the subset of big elements by a generalized characteristic function in which instead of the Boolean algebra {0,1} we can consider, for example, the interval [0,1]. The following is a precise definition. | An attempt to give an answer to such a question was proposed in 1965 by Lotfi Zadeh and at the same time, by Dieter Klaua in the framework of multi-valued logic. Now recall that the ''[[characteristic function]]'' of a classical subset ''X'' of ''S'' is the map ''c''<sub>X</sub> : → {0,1} such that ''c<sub>X</sub>''(''x'') = 1 if ''x'' is an element in ''X'' and ''c<sub>X</sub>''(''x'') = 0 otherwise. Obviously, it is possible to identify every subset ''X'' with its characteristic function ''c<sub>X</sub>'' and therefore the extension of a property with a suitable characteristic function. This suggests that we can define the subset of big elements by a generalized characteristic function in which instead of the Boolean algebra {0,1} we can consider, for example, the interval [0,1]. The following is a precise definition. | ||
'''Definition.''' Let ''S'' be a nonempty set, then | '''Definition.''' Let ''S'' be a nonempty set, then a ''fuzzy subset'' of ''S'' is a map ''s'' from ''S'' into [0,1]. We denote by [0,1]<sup>S</sup> the class of all the fuzzy subsets of ''S''. If S<sub>1</sub>,...S<sub>n</sub> are nonempty sets then a fuzzy subset of S<sub>1</sub>×. . .×S<sub>n</sub> is called an ''n-ary L-relation''. | ||
The elements in [0,1] are interpreted as truth values and, in accordance, for every ''x'' in ''S'', the number ''s(x)'' is interpreted as the membership degree of ''x'' to ''s''. We say that a fuzzy subset ''s'' is ''crisp'' if ''s''(''x'') is in {0,1} for every ''x'' in S. By associating every classical subsets of ''S'' with its characteristic function, we can identify the subsets of ''S'' with the crisp fuzzy subsets. In particular we call ''"empty subset"'' of ''S'' the fuzzy subset of ''S'' constantly equal to 0. Notice that in such a way there is not a unique empty subsets. | The elements in [0,1] are interpreted as truth values and, in accordance, for every ''x'' in ''S'', the number ''s(x)'' is interpreted as the membership degree of ''x'' to ''s''. We say that a fuzzy subset ''s'' is ''crisp'' if ''s''(''x'') is in {0,1} for every ''x'' in S. By associating every classical subsets of ''S'' with its characteristic function, we can identify the subsets of ''S'' with the crisp fuzzy subsets. In particular we call ''"empty subset"'' of ''S'' the fuzzy subset of ''S'' constantly equal to 0. Notice that in such a way there is not a unique empty subsets. | ||
Revision as of 11:30, 5 January 2009
To be Completed !! Template:TOC-right
Introduction
The term fuzzy subset is a generalization of the subset concept from set theory. Observe that we can obtain a subset of a given set S by considering the extension of a well defined property P in S. Indeed, the axiom of comprehension reads that a subset B of S exists whose members are precisely those objects in S satisfying P. For example if S is the set of natural numbers and P is the property "to be prime", then the subset B of prime numbers is defined. Assume that P is a vague property as "to be big", "to be young": is there a way to define the extension of P ? For example:
- is there a precise definition of the notion of set of big numbers ?
The notion of fuzzy subset
An attempt to give an answer to such a question was proposed in 1965 by Lotfi Zadeh and at the same time, by Dieter Klaua in the framework of multi-valued logic. Now recall that the characteristic function of a classical subset X of S is the map cX : → {0,1} such that cX(x) = 1 if x is an element in X and cX(x) = 0 otherwise. Obviously, it is possible to identify every subset X with its characteristic function cX and therefore the extension of a property with a suitable characteristic function. This suggests that we can define the subset of big elements by a generalized characteristic function in which instead of the Boolean algebra {0,1} we can consider, for example, the interval [0,1]. The following is a precise definition.
Definition. Let S be a nonempty set, then a fuzzy subset of S is a map s from S into [0,1]. We denote by [0,1]S the class of all the fuzzy subsets of S. If S1,...Sn are nonempty sets then a fuzzy subset of S1×. . .×Sn is called an n-ary L-relation.
The elements in [0,1] are interpreted as truth values and, in accordance, for every x in S, the number s(x) is interpreted as the membership degree of x to s. We say that a fuzzy subset s is crisp if s(x) is in {0,1} for every x in S. By associating every classical subsets of S with its characteristic function, we can identify the subsets of S with the crisp fuzzy subsets. In particular we call "empty subset" of S the fuzzy subset of S constantly equal to 0. Notice that in such a way there is not a unique empty subsets.
Some set-theoretical notions for fuzzy subsets
In classical mathematics the definitions of union, intersection and complement are related with the interpretation of the basic logical connectives . In order to define the same operations for fuzzy subsets, we have to fix suitable operations and ~ in [0,1] to interpret these connectives. Once this was done, we can set
- ,
- ,
- .
In such a way an algebraic structure is defined and this structure is the direct power of the structure ~,0 ,1) with index set S. In Zadeh's original papers the operations , ~ are defined by setting for every x and y in [0,1]:
- = min(x, y) ; = max(x,y) ; = 1-x.
In such a case is a complete, completely distributive lattice with an involution. Several authors prefer to consider different operations, as an example to assume that is a triangular norm in [0,1] and that is the corresponding triangular co-norm.
In all the cases the interpretation of a logical connective is conservative in the sense that its restriction to {0,1} coincides with the classical one. This entails that the map associating any subset X of a set S with the related characteristic function is an embedding of the Boolean algebra into the algebra .
L-subsets
The notion of fuzzy subset can be extended by substituting the interval [0,1] by any bounded lattice L. Again one assumes that in L suitable operations are defined to interpret the logical connectives. This extension was done mainly in the framework of fuzzy logic.
See also
- Fuzzy logic
- Fuzzy control system
- Neuro-fuzzy
- Fuzzy subalgebra
- Fuzzy associative matrix
- FuzzyCLIPS expert system
- Paradox of the heap
- Pattern recognition
- Rough set
Bibliography
- Cox E., The Fuzzy Systems Handbook (1994), ISBN 0-12-194270-8
- Elkan C.. The Paradoxical Success of Fuzzy Logic. November 1993. Available from Elkan's home page.
- Gerla G., Fuzzy logic: Mathematical Tools for Approximate Reasoning, Kluwer, 2001.
- Gottwald S., A treatase on Multi-Valued Logics, Research Studies Press LTD, Baldock 2001.
- Hájek P., Metamathematics of fuzzy logic. Kluwer 1998.
- Höppner F., Klawonn F., Kruse R. and Runkler T., Fuzzy Cluster Analysis (1999), ISBN 0-471-98864-2.
- Klaua D., Über einen Ansatz zur mehrwertigen Mengenlehre, Monatsberichte der Deutschen Akademie der Wissenschaften Berlin, vol 7 (1965), pp 859-867.
- Klir G. and Folger T., Fuzzy Sets, Uncertainty, and Information (1988), ISBN 0-13-345984-5.
- Klir G. , UTE H. St. Clair and Bo Yuan Fuzzy Set Theory Foundations and Applications,1997.
- Klir G. and Bo Yuan, Fuzzy Sets and Fuzzy Logic (1995) ISBN 0-13-101171-5
- Kosko B., Fuzzy Thinking: The New Science of Fuzzy Logic (1993), Hyperion. ISBN 0-7868-8021-X
- Novák V., Perfilieva I, Mockor J., Mathematical Principles of Fuzzy Logic, Kluwer Academic Publishers, Dordrecht, (1999).
- Yager R. and Filev D., Essentials of Fuzzy Modeling and Control (1994), ISBN 0-471-01761-2
- Zimmermann H., Fuzzy Set Theory and its Applications (2001), ISBN 0-7923-7435-5.
- Zadeh L.A., Fuzzy Sets, Information and Control, 8 (1965) 338-353.





![{\displaystyle ([0,1]^{S},\cup ,\cap ,-,\emptyset ,S)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2c3527a01030236ef22bc844e1d84e265470e6b)
![{\displaystyle ([0,1],\oplus ,\otimes ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a578615e200bb0fe3e715b9d50d32107f5ff5841)



![{\displaystyle ([0,1]^{F},\cup ,\cap ,-,\emptyset ,S)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8187875116d25b16cd1e44f84a9eb119a1446af)



