User:Dmitrii Kouznetsov/Analytic Tetration: Difference between revisions
imported>Dmitrii Kouznetsov (figure0) |
imported>Dmitrii Kouznetsov m (fig0) |
||
| Line 1: | Line 1: | ||
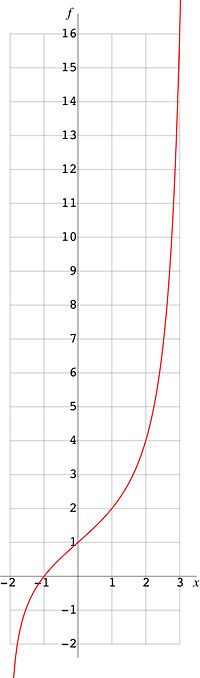
[[Image:AnalyticTetrtionBase2figure0.jpg|200px|right|thumb| | [[Image:AnalyticTetrtionBase2figure0.jpg|200px|right|thumb|Fig.0. Graphic of analytic tetration <math>f={\rm sex}_2(x)</math> at the real axis.]] | ||
<!-- | <!-- | ||
[[Image:ExampleEquationLog01.png|300px|right|thumb|FIg.1. Example of graphic solution of equation <math>L=\log_b(L)</math> for | [[Image:ExampleEquationLog01.png|300px|right|thumb|FIg.1. Example of graphic solution of equation <math>L=\log_b(L)</math> for | ||
Revision as of 07:45, 20 May 2008
Analytic tetration
by Dmitrii Kouznetsov.
Abstract
Analytic tetration is defined as mathematical function that coincides witht the tetration at integer values of the argument and is analytic outside the negative part of the real axis. Existence of such a function is postulated; and arguments in favor of uniqueness of such a function are considered. The algorithm of evaluation is suggested. Examples of evaluation, pictures and tables are supplied. The application and the generalization is discussed.
Preface
The colleagues indicated so many misprints in my papers about tetration, posted at my homepage [1], that I want to give them opportunity to correct them in real time.
I consider the topic very important and urgent. The analytic tetration should be investigated and discussed right now; overvice, the non-analytic extension may become an ugly standard in mathematics of computation; the implementation of hige numbers with non-analycit tetration would make difficult realization of arithmetic operations and cause a lot of incompatibilities.
This is my apology for posting this research now, while the rigorous proof of existence and uniqueness of the analytic tetration is not yet found. My believe is based on the numerical check of the hypothesis of the existence and uniqueness, on smallness of the residual at the substitution of the function to the tetration equation and beauty of the resulting pictures. I cannot imagine that the agreement with 14 decimal digits occurs just by occasion without deep mathematical meaning.
In such a way I apologize for postulating of statements which should be prooven by the rigorous mathematical deduction.
Introduction
Asymptotic
Variety of tertations
Eigenvalues of logarithm
I search for the simplest solution, that asymptotically, approaches the eigenvalue of logarithm. For slightly larger than unity, there exist real sloutions, as it is shown in figure 1.
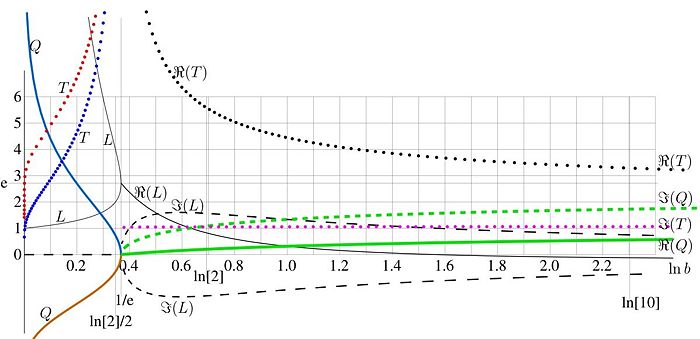
For , there are 2 complex solutions shown in figure 2.
Asymptotocs versus fiting
Approximation
Cauchi integral
Base e
Base 2
Large base. Base 10
Small base. Base
Discussion
Conclusions
references
- ↑ Publications (Those about tetrations are at the top) http://www.ils.uec.ac.jp/~dima/PAPERS