Equation (mathematics): Difference between revisions
imported>Richard Pinch m (sp) |
imported>Jitse Niesen (rewrite lead section, mainly to simplify first paragraph) |
||
| Line 1: | Line 1: | ||
{{subpages}} | {{subpages}} | ||
In [[mathematics]], an '''equation''' is a | In [[mathematics]], an '''equation''' is a statement that two quantities are equal. It is usually regarded as a kind of mathematical problem in which you have to find a value which makes the equation true. A simple example is the question: What do you have to fill in on the dots in … + 2 = 3? The answer is 1, because 1 + 2 = 3. The unknown quantity in such problems is frequently denotes be a letter, often ''x'', so that the equation becomes ''x'' + 2 = 3. The solution of this equation is ''x'' = 1. | ||
By contrast, an '''identity''' is an equality which is stated to be universally true for all permissible values of the variables, rather than representing a condition on those values. For example, <math>x+y = y+x</math> is an identity for real | By contrast, an '''identity''' is an equality which is stated to be universally true for all permissible values of the variables, rather than representing a condition on those values. For example, <math>x+y = y+x</math> is an identity for [[real number]]s, since it is true for all real values of ''x'' and ''y''. | ||
Technically, an equation has to indicate what values the unknown variable can take; this is called the ''domain'' of the variable. In the example ''x'' + 2 = 3, it may be specified that <math>x</math> is a real number. Often, the domain is not specified explicitly, but it is assumed that the reader knows what it is supposed to be. | |||
The equation may have no solution, may have one solution and may have many solutions, depending on the form of the equations and the domain of the unknown variable. | |||
[[Science|Scientific]] laws are often formulated as equations, especially in [[physics]] and other [[natural sciences]]. Examples are [[Newton's laws]], the equation of a [[harmonic oscillator]] and the [[Schrödinger equation]]. | |||
The term ''equation'' is used also in [[chemistry]], indicating conservation of atomic or [[isotopic content|isotopic]] content at the [[chemical reaction]]s. | |||
==Examples== | |||
The equation may have the form | The equation may have the form | ||
| Line 9: | Line 18: | ||
:(2) <math>F(x)=G(x)</math> | :(2) <math>F(x)=G(x)</math> | ||
where <math> F </math> and <math>G</math> are [[known function]]s and <math>x</math> is the [[unknown variable]]. | where <math> F </math> and <math>G</math> are [[known function]]s and <math>x</math> is the [[unknown variable]]. | ||
For function <math>F(x)=1+x</math>, the equation (1) has no solutions among [[natural number]]s, but has solution | For function <math>F(x)=1+x</math>, the equation (1) has no solutions among [[natural number]]s, but has solution | ||
Revision as of 06:19, 6 May 2009
In mathematics, an equation is a statement that two quantities are equal. It is usually regarded as a kind of mathematical problem in which you have to find a value which makes the equation true. A simple example is the question: What do you have to fill in on the dots in … + 2 = 3? The answer is 1, because 1 + 2 = 3. The unknown quantity in such problems is frequently denotes be a letter, often x, so that the equation becomes x + 2 = 3. The solution of this equation is x = 1.
By contrast, an identity is an equality which is stated to be universally true for all permissible values of the variables, rather than representing a condition on those values. For example, is an identity for real numbers, since it is true for all real values of x and y.
Technically, an equation has to indicate what values the unknown variable can take; this is called the domain of the variable. In the example x + 2 = 3, it may be specified that is a real number. Often, the domain is not specified explicitly, but it is assumed that the reader knows what it is supposed to be.
The equation may have no solution, may have one solution and may have many solutions, depending on the form of the equations and the domain of the unknown variable.
Scientific laws are often formulated as equations, especially in physics and other natural sciences. Examples are Newton's laws, the equation of a harmonic oscillator and the Schrödinger equation. The term equation is used also in chemistry, indicating conservation of atomic or isotopic content at the chemical reactions.
Examples
The equation may have the form
- (1)
or
- (2)
where and are known functions and is the unknown variable.
For function , the equation (1) has no solutions among natural numbers, but has solution in the set of integer numbers.
Equation has no solutions among rational numbers, has one solution () among positive real numbers, and has two soluitons ( and ) among real numbers.
Inverse function
Function in equation (1) ; or functions and in equation (2) may also depend on some parameter(s). In this case, the solution(s) also may depend on parameter(s). Indicating the function, the parameter, say, , can be specified as a second argument, writing , or as subscript, writing , .
In relatively simple cases, function depends only on the unknown variable, and depends on the parameter; for example,
(3) .
In this case, the solution is considered as an inverse function of , which can be written as
(4) .
Dependending on the function , range of values of and set , there may exist no inverse function, one inverse function or several inverse functions.
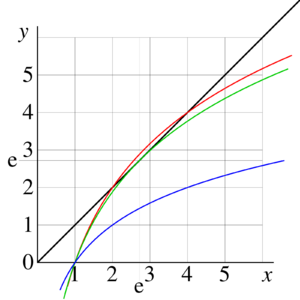
Graphical solution of equations
Solving equations, it may worth to begin with graphic solution of the equation, which allows the quick and dirty estimates. One plots both functions, and at the same graphic, and watch the point (s) of the intersection of the curves. In figire 1, functions is plotted with black line, and function is plotted with red curve. The intersections with black curve indicate values of which are solutions.
At the same figure, the cases (only one solution, ) and (no solutions among real numbers) are shown with green and blue curves.
System of equations
In the equations (1) or (2), may denote several numbers at once, ; and functions and may return values from multidimentional space . In this case, one says that there is system of equations. For example, there is well developed theory of systems of linear equations, while unknown variables are real or complex numbers.
Differential equations and integral equations
In particular, the variable may denote a function of one or several variables, so that the set of p[ossible values is some Hilbert space; the function is then an operator on this space which may be expressed in terms of derivatives or integrals of the function elements. In these cases, the equation is called a differential equation or an integral equation.
Operator equations
Equations can be used for objects of any origin, as soon, as the operation of equality is defined. In particular, in Quantum mechanics, the Heisenberg equation deals with non-commuting objects (operators).