User talk:Paul Wormer/scratchbook1: Difference between revisions
imported>Paul Wormer No edit summary |
imported>Paul Wormer |
||
| Line 54: | Line 54: | ||
===Proof that entropy is a state function=== | ===Proof that entropy is a state function=== | ||
Equation [[#(1)|(1)]] gives the sufficient condition that the entropy ''S'' is a state function. The standard proof, as given now, is physical, by means of [[Carnot cycle]]s, and is based on the | Equation [[#(1)|(1)]] gives the sufficient condition that the entropy ''S'' is a state function. The standard proof of equation (1), as given now, is physical, by means of an engine making [[Carnot cycle]]s, and is based on the Kelvin formulation of the [[second law of thermodynamics]]. | ||
{{Image|Entropy.png|right| | {{Image|Entropy.png|right|250px}} | ||
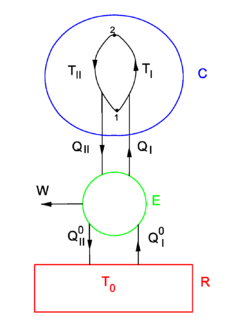
Consider the figure. A system, consisting of an arbitrary closed system ''C'' (only heat goes in and out) and a reversible heat engine ''E'', is coupled to a large heat reservoir ''R'' of constant temperature ''T''<sub>0</sub>. The system ''C'' undergoes a cyclic state change 1-2-1. Since no work is performed on or by ''C'', it follows that | |||
:<math> | |||
Q_\mathrm{I} =Q_\mathrm{II} \quad\hbox{with}\quad Q_\mathrm{I} \equiv \int_1^2 DQ_\mathrm{I},\quad Q_\mathrm{II} \equiv \int_1^2 DQ_\mathrm{II}. | |||
</math> | |||
For the heat engine ''E'' it holds (by the definition of [[thermodynamic temperature]]) that | |||
:<math> | |||
\frac{DQ_\mathrm{I}}{DQ^0_\mathrm{I}} = \frac{T_\mathrm{I}}{T_0}\quad\hbox{and}\quad | |||
\frac{DQ_\mathrm{\mathrm{II}}}{DQ^0_\mathrm{II}} = \frac{T_\mathrm{II}}{T_0} . | |||
</math> | |||
Hence | |||
:<math> | |||
\frac{Q^0_\mathrm{I}}{T_0} \equiv \frac{1}{T_0} \int_1^2 DQ^0_\mathrm{I} = \int_1^2 \frac{DQ_\mathrm{I}}{T_\mathrm{I}} | |||
\quad\hbox{and}\quad | |||
\frac{Q^0_\mathrm{II}}{T_0} \equiv \frac{1}{T_0} \int_1^2 DQ^0_\mathrm{II} = \int_1^2 \frac{DQ_\mathrm{II}}{T_\mathrm{II}} . | |||
</math> | |||
From Kelvin's principle it follows that ''W'' is necessarily less or equal zero, because there is only the single heat source ''R''. Invoking the first law of thermodynamics we get, | |||
:<math> | |||
W = Q^0_\mathrm{I} - Q^0_\mathrm{II} \le 0\; \Longrightarrow\; \frac{Q^0_\mathrm{I}}{T_0} \le \frac{Q^0_\mathrm{II}}{T_0}, | |||
</math> | |||
so that | |||
:<math> | |||
\int_1^2 \frac{DQ_\mathrm{I}}{T_\mathrm{I}} \le \int_1^2 \frac{DQ_\mathrm{II}}{T_\mathrm{II}} | |||
</math> | |||
Because the processes inside ''C'' and ''E'' are assumed reversible, all arrows can be reverted and in the very same way it is shown that | |||
:<math> | |||
\int_1^2 \frac{DQ_\mathrm{II}}{T_\mathrm{II}} \le \int_1^2 \frac{DQ_\mathrm{I}}{T_\mathrm{I}}, | |||
</math> | |||
so that equation (1) holds (with a slight change of notation, subscripts are transferred to the respective integral signs): | |||
:<math>{\int\limits_1\limits^2}_{{\!\!}^{(I)}}\frac{DQ}{T} = {\int\limits_1\limits^2}_{{\!\!}^{(II)}} \frac{DQ}{T} . | |||
</math> | |||
A Carnot engine performs reversible cycles (in the state space of E, not be confused with cycles in the state space of C) and per cycle either generates work ''DW''<sub>out</sub> when heat is transported from | |||
<!-- | |||
{{Image|Entropy.png|right|350px|Fig. 1. ''T'' > ''T''<sub>0</sub>. (I): Carnot engine ''E'' moves heat from heat reservoir ''R'' to closed system ''C'' and needs input of work ''DW''<sub>in</sub>. (II): ''E'' generates work ''DW''<sub>out</sub> from the heat flow from ''C'' to ''R''. }}. | |||
In figure 1 a closed system ''C'' (of constant volume and variable temperature ''T'') is shown. It is connected to an infinite heat reservoir ''R'' through a reversible Carnot engine ''E''. Because ''R'' is infinite, its temperature ''T''<sub>0</sub> is constant, addition or extraction of heat does not change ''T''<sub>0</sub>. Without loss of generality it can be assumed that ''T'' > ''T''<sub>0</sub>, then path I in figure 1 gives transport of heat from low to high temperature and path II form high to low. If it is assumed that | |||
A Carnot engine performs reversible cycles (in the state space of ''E'', not to be confused with cycles in the state space of ''C'') and per cycle either generates work ''DW''<sub>out</sub> when heat is transported from ''C'' to ''R'' (II), or needs work ''DW''<sub>in</sub> when heat is transported from low to high temperature (I), in accordance with the Clausius/Kelvin formulation of the second law. | |||
The definition of [[thermodynamical temperature]] (a positive quantity) is such that for II, | The definition of [[thermodynamical temperature]] (a positive quantity) is such that for II, | ||
| Line 122: | Line 160: | ||
</math> | </math> | ||
is a state (local) variable. | is a state (local) variable. | ||
--> | |||
==Footnotes== | ==Footnotes== | ||
<references /> | <references /> | ||
==References == | ==References == | ||
* M. W. Zemansky, ''Kelvin and Caratheodory—A Reconciliation'', American Journal of Physics Vol. '''34''', pp. 914-920 (1966) [http://dx.doi.org/10.1119/1.1972279] | * M. W. Zemansky, ''Kelvin and Caratheodory—A Reconciliation'', American Journal of Physics Vol. '''34''', pp. 914-920 (1966) [http://dx.doi.org/10.1119/1.1972279] | ||
Revision as of 08:47, 5 November 2009
Entropy is a function of the state of a thermodynamic system. It is a size-extensive[1] quantity with dimension energy divided by temperature (SI unit: joule/K). Entropy has no clear analogous mechanical meaning—unlike volume, a similar size-extensive state parameter with dimension energy divided by pressure. Moreover entropy cannot directly be measured, there is no such thing as an entropy meter, whereas state parameters as volume and temperature are easily determined. Consequently entropy is one of the least understood concepts in physics.[2]
The state variable "entropy" was introduced by Rudolf Clausius in the 1860s[3] when he gave a mathematical formulation of the second law of thermodynamics. He derived the name from the classical Greek ἐν + τροπή (en = in, at; tropè = change, transformation). On purpose Clausius chose a term similar to "energy", because of the close relationship between the two concepts.
The traditional way of introducing entropy is by means of a Carnot engine, an abstract engine conceived in 1824 by Sadi Carnot[4] as an idealization of a steam engine. Carnot's work foreshadowed the second law of thermodynamics. The "engineering" manner of introducing entropy through an engine will be discussed below. In this approach, entropy is the amount of heat (per degree kelvin) gained or lost by a thermodynamic system that makes a transition from one state to another.
In 1877 Ludwig Boltzmann[5] gave a definition of entropy in the context of the kinetic gas theory, a branch of physics that developed into statistical thermodynamics. Boltzmann's definition of entropy was furthered by John von Neumann[6] to a quantum statistical definition. The quantum statistical point of view, too, will be reviewed in the present article. In the statistical approach the entropy of an isolated (constant energy) system is kB lnΩ, where kB is Boltzmann's constant, Ω is the number of different wave functions of the system belonging to the system's energy (Ω is the degree of degeneracy, the probability that a state is described by one of the Ω wave functions), and the function ln stands for the natural (base e) logarithm.
Not satisfied with the engineering type of argument, the mathematician Constantin Carathéodory gave in 1909 a new axiomatic formulation of entropy and the second law.[7] His theory was based on Pfaffian differential equations. His axiom replaced the earlier Kelvin-Planck and the equivalent Clausius formulation of the second law and did not need Carnot engines. Caratheodory's work was taken up by Max Born,[8] and it is treated in a few textbooks.[9] Since it requires more mathematical knowledge than the traditional approach based on Carnot engines, and since this mathematical knowledge is not needed by most students of thermodynamics, the traditional approach is still dominant in the majority of introductory works on thermodynamics.
Classical definition
The state (a point in state space) of a thermodynamic system is characterized by a number of variables, such as pressure p, temperature T, amount of substance n, volume V, etc. Any thermodynamic parameter can be seen as a function of an arbitrary independent set of other thermodynamic variables, hence the terms "property", "parameter", "variable" and "function" are used interchangeably. The number of independent thermodynamic variables of a system is equal to the number of energy contacts of the system with its surroundings.
An example of a reversible (quasi-static) energy contact is offered by the prototype thermodynamical system, a gas-filled cylinder with piston. Such a cylinder can perform work on its surroundings,
where dV stands for a small increment of the volume V of the cylinder, p is the pressure inside the cylinder and DW stands for a small amount of work. Work by expansion is a form of energy contact between the cylinder and its surroundings. This process can be reverted, the volume of the cylinder can be decreased, the gas is compressed and the surroundings perform work DW = pdV < 0 on the cylinder.
The small amount of work is indicated by D, and not by d, because DW is not necessarily a differential of a function. However, when we divide DW by p the quantity DW/p becomes obviously equal to the differential dV of the differentiable state function V. State functions depend only on the actual values of the thermodynamic parameters (they are local in state space), and not on the path along which the state was reached (the history of the state). Mathematically this means that integration from point 1 to point 2 along path I in state space is equal to integration along a different path II,
The amount of work (divided by p) performed reversibly along path I is equal to the amount of work (divided by p) along path II. This condition is necessary and sufficient that DW/p is the differential of a state function. So, although DW is not a differential, the quotient DW/p is one.
Reversible absorption of a small amount of heat DQ is another energy contact of a system with its surroundings; DQ is again not a differential of a certain function. In a completely analogous manner to DW/p, the following result can be shown for the heat DQ (divided by T) absorbed reversibly by the system along two different paths (along both paths the absorption is reversible):
(1)
Hence the quantity dS defined by
is the differential of a state variable S, the entropy of the system. In the next subsection equation (1) will be proved from the Clausius/Kelvin principle. Observe that this definition of entropy only fixes entropy differences:
Note further that entropy has the dimension energy per degree temperature (joule per degree kelvin) and recalling the first law of thermodynamics (the differential dU of the internal energy satisfies dU = DQ − DW), it follows that
(For convenience sake only a single work term was considered here, namely DW = pdV, work done by the system). The internal energy is an extensive quantity. The temperature T is an intensive property, independent of the size of the system. It follows that the entropy S is an extensive property. In that sense the entropy resembles the volume of the system. We reiterate that volume is a state function with a well-defined mechanical meaning, whereas entropy is introduced by analogy and is not easily visualized. Indeed, as is shown in the next subsection, it requires a fairly elaborate reasoning to prove that S is a state function, i.e., that equation (1) holds.
Proof that entropy is a state function
Equation (1) gives the sufficient condition that the entropy S is a state function. The standard proof of equation (1), as given now, is physical, by means of an engine making Carnot cycles, and is based on the Kelvin formulation of the second law of thermodynamics.
Consider the figure. A system, consisting of an arbitrary closed system C (only heat goes in and out) and a reversible heat engine E, is coupled to a large heat reservoir R of constant temperature T0. The system C undergoes a cyclic state change 1-2-1. Since no work is performed on or by C, it follows that
For the heat engine E it holds (by the definition of thermodynamic temperature) that
Hence
From Kelvin's principle it follows that W is necessarily less or equal zero, because there is only the single heat source R. Invoking the first law of thermodynamics we get,
so that
Because the processes inside C and E are assumed reversible, all arrows can be reverted and in the very same way it is shown that
so that equation (1) holds (with a slight change of notation, subscripts are transferred to the respective integral signs):
Footnotes
- ↑ A size-extensive property of a system becomes x times larger when the system is enlarged by a factor x, provided all intensive parameters remain the same upon the enlargement. Intensive parameters, like temperature, density, and pressure, are independent of size.
- ↑ It is reported that in a conversation with Claude Shannon, John (Johann) von Neumann said: "In the second place, and more important, nobody knows what entropy really is [..]”. M. Tribus, E. C. McIrvine, Energy and information, Scientific American, vol. 224 (September 1971), pp. 178–184.
- ↑ R. J. E. Clausius, Abhandlungen über die mechanische Wärmetheorie [Treatise on the mechanical theory of heat], two volumes, F. Vieweg, Braunschweig, (1864-1867).
- ↑ S. Carnot, Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance (Reflections on the motive power of fire and on machines suited to develop that power), Chez Bachelier, Paris (1824).
- ↑ L. Boltzmann, Über die Beziehung zwischen dem zweiten Hauptsatz der mechanischen Wärmetheorie und der Wahrscheinlichkeitsrechnung respektive den Sätzen über das Wärmegleichgewicht, [On the relation between the second fundamental law of the mechanical theory of heat and the probability calculus with respect to the theorems of heat equilibrium] Wiener Berichte vol. 76, pp. 373-435 (1877)
- ↑ J. von Neumann, Mathematische Grundlagen der Quantenmechnik, [Mathematical foundation of quantum mechanics] Springer, Berlin (1932)
- ↑ C. Carathéodory, Untersuchungen über die Grundlagen der Thermodynamik [Investigation on the foundations of thermodynamics], Mathematische Annalen, vol. 67, pp. 355-386 (1909).
- ↑ M. Born, Physikalische Zeitschrift, vol. 22, p. 218, 249, 282 (1922)
- ↑ H. B. Callen, Thermodynamics and an Introduction to Thermostatistics. John Wiley and Sons, New York, 2nd edition, (1965); E. A. Guggenheim, Thermodynamics, North-Holland, Amsterdam, 5th edition (1967)
References
- M. W. Zemansky, Kelvin and Caratheodory—A Reconciliation, American Journal of Physics Vol. 34, pp. 914-920 (1966) [1]