Envelope function: Difference between revisions
imported>John R. Brews (See...also) |
imported>John R. Brews (beating waves) |
||
| Line 4: | Line 4: | ||
{{See also|Modulation}} | {{See also|Modulation}} | ||
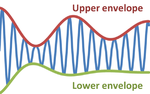
In [[physics]] and [[engineering]], the '''envelope function''' of a rapidly varying [[Signal (communications)|signal]] is a smooth curve outlining its extremes in amplitude.<ref name=Johnson/> The figure illustrates a sine wave varying between an upper and a lower envelope. The envelope function may be a function of time, or of space, or indeed of any variable. | In [[physics]] and [[engineering]], the '''envelope function''' of a rapidly varying [[Signal (communications)|signal]] is a smooth curve outlining its extremes in amplitude.<ref name=Johnson/> The figure illustrates a sine wave varying between an upper and a lower envelope. The envelope function may be a function of time, or of space, or indeed of any variable. | ||
==Example: Beat frequency== | |||
{{see also|Beat (acoustics)}} | |||
{{Image|Modulated wave.png|right|150px|A modulated wave resulting from adding two sine waves of nearly identical wavelength and frequency.}} | |||
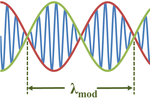
A common situation resulting in an envelope function in both space ''x'' and time ''t'' is the superposition of two waves of almost the same wavelength and frequency:<ref name=Kinsman> | |||
{{cite book |title=Wind Waves: Their Generation and Propagation on the Ocean Surface |author=Blair Kinsman |year=2002 |url=http://books.google.com/books?id=RlhZc4HAS5oC&pg=PA186 |pages=p. 186 |publisher=Courier Dover Publications |isbn=0486495116 |edition=Reprint of Prentice-Hall 1965}} | |||
</ref> | |||
:<math>F(x, \ t) = \sin \left[ 2 \pi \left( \frac {x}{\lambda - \Delta \lambda } - ( f + \Delta f )t \right) \right] </math><math>+ \sin \left[ 2 \pi \left( \frac {x}{\lambda + \Delta \lambda } - ( f - \Delta f )t \right) \right] </math> | |||
:::<math>\approx 2\cos \left[ 2 \pi \left( \frac {x} {\lambda_{mod}} - \Delta f \ t \right) \right] \ \sin \left[ 2 \pi \left( \frac {x}{\lambda} - f \ t \right) \right] \ , </math> | |||
which uses the trigonometric formula for the addition of two sine waves, and the approximation Δλ<<λ: | |||
:<math>\frac{1}{\lambda \pm \Delta \lambda}=\frac {1}{\lambda}\ \frac{1}{1\pm\Delta \lambda / \lambda }\approx \frac{1}{\lambda}\mp \frac {\Delta \lambda}{\lambda^2} .</math> | |||
Here the ''modulation wavelength'' λ<sub>mod</sub> is given by:<ref name=Kinsman/><ref name=Denny> | |||
{{cite book |title=Air and Water: The Biology and Physics of Life's Media |author=Mark W. Denny |url=http://books.google.com/books?id=XjNS6v7q130C&pg=PA289 |pages=p. 289 |publisher=Princeton University Press | |||
|isbn=0691025185 |year=1993}} | |||
</ref> | |||
:<math> \lambda_{mod} = \frac {\lambda^2}{\Delta \lambda}\ . </math> | |||
The modulation wavelength is double that of the envelope itself because each half-wavelength of the modulating cosine wave governs both positive and negative values of the modulated sine wave. | |||
If this wave is a sound wave, the ear hears the frequency associated with ''f'' and the amplitude of this sound varies with the ''beat frequency'' Δ''f''.<ref name=Tipler/> | |||
===Phase and group velocity=== | |||
The argument of the sinusoids above apart from a factor 2π are: | |||
:<math>\xi_c =\left( \frac {x}{\lambda} - f \ t \right)\ , </math> | |||
:<math>\xi_e=\left( \frac {x} {\lambda_{mod}} - \Delta f \ t \right) \ , </math> | |||
with subscripts ''c'' and ''e'' referring to the ''carrier'' and the ''envelope''. The same values for these functions occur when these arguments increase by unity, whether that increase is a result of an increase in distance ''x'' or an increase in time ''t''. That is, the same amplitude results for ξ<sub>c</sub> and for ξ<sub>c</sub> + 1, and likewise for ξ<sub>b</sub>. This invariance means that one can trace these waveforms in space to find a position of fixed amplitude propagates in time with a speed that keeps ξ fixed; that is, for the carrier: | |||
:<math>\left( \frac {x}{\lambda} - f \ t \right) = \left( \frac {x+\Delta x}{\lambda} - f (t + \Delta t) \right)\ , </math> | |||
which determines for a constant amplitude the distance Δ''x'' is related to the time interval Δ''t'' by the so-called ''phase velocity'' ''v<sub>p</sub>'' | |||
:<math>v_p = \frac{\Delta x}{\Delta t} = \lambda f \ . </math> | |||
On the other hand, the same considerations show the envelope propagates at the so-called ''group velocity'' ''v<sub>g</sub>'':<ref name=Eberly/> | |||
:<math>v_g = \frac{\Delta x}{\Delta t} = \lambda_{mod}\Delta f =\lambda^2 \frac{\Delta f}{\Delta \lambda} \ . </math> | |||
A more common expression for the group velocity is obtained by introducing the ''wavevector'' ''k'': | |||
:<math>k=\frac{2\pi}{\lambda} \ . </math> | |||
We notice that for small changes Δλ, the magnitude of the corresponding small change in wavevector: | |||
:<math> \Delta k = \left|\frac{dk}{d\lambda}\right| = 2\pi \frac{\Delta \lambda}{\lambda^2} \ , </math> | |||
so the group velocity can be rewritten as: | |||
:<math> v_g= \frac {2\pi\Delta f}{\Delta k} \ . </math> | |||
In so-called ''dispersive media'' the frequency and wavevector are related by a ''dispersion relation'', 2π''f'' ≡ ω = ω(''k''), and the group velocity can be written: | |||
:<math>v_g =\frac{d\omega (k)}{dk} \ . </math> | |||
Here ω is the frequency in radians/s. | |||
==References== | ==References== | ||
{{reflist|refs= | {{reflist|refs= | ||
<ref name=Eberly> | |||
{{cite book |title=Laser Physics |author=Peter W. Milonni, Joseph H. Eberly |url=http://books.google.com/books?id=f7g0Mx5RR3cC&pg=PA336 |pages=p. 336 |chapter=§8.3 Group velocity |isbn=0470387718 |year=2010 |publisher=John Wiley & Sons |edition=2nd ed}} | |||
</ref> | |||
<ref name=Johnson> | <ref name=Johnson> | ||
| Line 12: | Line 61: | ||
</ref> | </ref> | ||
<ref name=Tipler > | |||
{{cite book |url=http://books.google.com/books?id=BMVR37-8Jh0C&pg=PA538 |pages=p. 538 |isbn=142920124X |publisher=Macmillan |year=2008 |author=Paul Allen Tipler, Gene Mosca |edition=6th ed |title=Physics for Scientists and Engineers, Volume 1}} | |||
</ref> | |||
}} | }} | ||
Revision as of 11:03, 8 April 2012
- See also: Modulation
In physics and engineering, the envelope function of a rapidly varying signal is a smooth curve outlining its extremes in amplitude.[1] The figure illustrates a sine wave varying between an upper and a lower envelope. The envelope function may be a function of time, or of space, or indeed of any variable.
Example: Beat frequency
- See also: Beat (acoustics)
A common situation resulting in an envelope function in both space x and time t is the superposition of two waves of almost the same wavelength and frequency:[2]
which uses the trigonometric formula for the addition of two sine waves, and the approximation Δλ<<λ:
Here the modulation wavelength λmod is given by:[2][3]
The modulation wavelength is double that of the envelope itself because each half-wavelength of the modulating cosine wave governs both positive and negative values of the modulated sine wave.
If this wave is a sound wave, the ear hears the frequency associated with f and the amplitude of this sound varies with the beat frequency Δf.[4]
Phase and group velocity
The argument of the sinusoids above apart from a factor 2π are:
with subscripts c and e referring to the carrier and the envelope. The same values for these functions occur when these arguments increase by unity, whether that increase is a result of an increase in distance x or an increase in time t. That is, the same amplitude results for ξc and for ξc + 1, and likewise for ξb. This invariance means that one can trace these waveforms in space to find a position of fixed amplitude propagates in time with a speed that keeps ξ fixed; that is, for the carrier:
which determines for a constant amplitude the distance Δx is related to the time interval Δt by the so-called phase velocity vp
On the other hand, the same considerations show the envelope propagates at the so-called group velocity vg:[5]
A more common expression for the group velocity is obtained by introducing the wavevector k:
We notice that for small changes Δλ, the magnitude of the corresponding small change in wavevector:
so the group velocity can be rewritten as:
In so-called dispersive media the frequency and wavevector are related by a dispersion relation, 2πf ≡ ω = ω(k), and the group velocity can be written:
Here ω is the frequency in radians/s.
References
- ↑ C. Richard Johnson, Jr, William A. Sethares, Andrew G. Klein (2011). “Figure C.1: The envelope of a function outlines its extremes in a smooth manner”, Software Receiver Design: Build Your Own Digital Communication System in Five Easy Steps. Cambridge University Press, p. 417. ISBN 0521189446.
- ↑ 2.0 2.1 Blair Kinsman (2002). Wind Waves: Their Generation and Propagation on the Ocean Surface, Reprint of Prentice-Hall 1965. Courier Dover Publications, p. 186. ISBN 0486495116.
- ↑ Mark W. Denny (1993). Air and Water: The Biology and Physics of Life's Media. Princeton University Press, p. 289. ISBN 0691025185.
- ↑ Paul Allen Tipler, Gene Mosca (2008). Physics for Scientists and Engineers, Volume 1, 6th ed. Macmillan, p. 538. ISBN 142920124X.
- ↑ Peter W. Milonni, Joseph H. Eberly (2010). “§8.3 Group velocity”, Laser Physics, 2nd ed. John Wiley & Sons, p. 336. ISBN 0470387718.
![{\displaystyle F(x,\ t)=\sin \left[2\pi \left({\frac {x}{\lambda -\Delta \lambda }}-(f+\Delta f)t\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0467cdce58d41ddf370525c035d69f994c3f10a4)
![{\displaystyle +\sin \left[2\pi \left({\frac {x}{\lambda +\Delta \lambda }}-(f-\Delta f)t\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/987cb6c9153bdae25867ffef6107a03ecc677376)
![{\displaystyle \approx 2\cos \left[2\pi \left({\frac {x}{\lambda _{mod}}}-\Delta f\ t\right)\right]\ \sin \left[2\pi \left({\frac {x}{\lambda }}-f\ t\right)\right]\ ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe71e240d4a8f95bb96ca9bfebc22f2be9fffabf)










