User:David MacQuigg/Sandbox/Separative Work Units: Difference between revisions
(draft section on SWU calculation) |
No edit summary |
||
| Line 1: | Line 1: | ||
== Calculation == | == Calculation == | ||
=== Simple Daemon Model === | |||
Imagine we have a daemon capable of separating isotopes by comparing their atomic masses, one pair of atoms at a time. This is a close relative of Maxwell's daemon, but non-ideal in that he requires a bit of energy <math>w_{1}</math> for each test separation. Let's put this daemon to work on a large number <math>N</math> of uranium atoms, where <math>N = N_a + N_b</math> a simple sum of the number of atoms that we want to separate into types a and b. | |||
The daemon works by grabbing random pairs of atoms passing by and comparing their masses. If the mixture is 50/50, then the separation will succeed 50% of the time, and the other 50% will be wasted on atoms that are the same. Total energy per successful separation will be <math>2w_1</math>. | |||
What if the mixture is not 50/50? Then energy will be wasted comparing atoms that are the same. The total energy per successful separation will be larger. If the fractions of uranium atoms in the mix are <math>x_a</math> and <math>x_b</math>, then the probability of a successful separation is <math>2x_ax_b</math>. Total energy per successful separation is then <math>w_1/(2x_ax_b)</math>. For a two-component mixture <math>x_a + x_b = 1</math> and we need only one variable <math>x = x_a</math> to define a "value function" as the ratio of work per separation compared to the optimum mixture <math>x = 1/2</math>. | |||
:<math>V(x) = 1/4{x(1-x)}</math> | |||
[https://docs.google.com/spreadsheets/d/1OyKPyjo6k1ckZVwAh8sfkDEtB5W22VUriBaelK3LWY4/edit?usp=sharing Fig.2] shows the energy per separation rising asymptotically as the fraction of the desired isotope approaches zero or one. | |||
=== Dirac's Thermodynamic Model === | |||
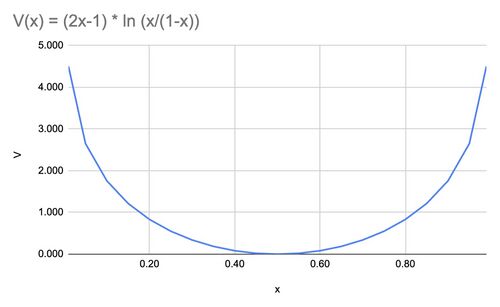
{{Image|SWUfunction.jpg|right|500px|Fig.1 Logarithmic function used in calculating Separative Work Units.}} | {{Image|SWUfunction.jpg|right|500px|Fig.1 Logarithmic function used in calculating Separative Work Units.}} | ||
SWUs are a function of the concentrations of the feedstock, the enriched output, and the depleted tailings. | SWUs are a function of the concentrations of the feedstock, the enriched output, and the depleted tailings. | ||
Revision as of 05:38, 4 August 2024
Calculation
Simple Daemon Model
Imagine we have a daemon capable of separating isotopes by comparing their atomic masses, one pair of atoms at a time. This is a close relative of Maxwell's daemon, but non-ideal in that he requires a bit of energy for each test separation. Let's put this daemon to work on a large number of uranium atoms, where a simple sum of the number of atoms that we want to separate into types a and b.
The daemon works by grabbing random pairs of atoms passing by and comparing their masses. If the mixture is 50/50, then the separation will succeed 50% of the time, and the other 50% will be wasted on atoms that are the same. Total energy per successful separation will be .
What if the mixture is not 50/50? Then energy will be wasted comparing atoms that are the same. The total energy per successful separation will be larger. If the fractions of uranium atoms in the mix are and , then the probability of a successful separation is . Total energy per successful separation is then . For a two-component mixture and we need only one variable to define a "value function" as the ratio of work per separation compared to the optimum mixture .
Fig.2 shows the energy per separation rising asymptotically as the fraction of the desired isotope approaches zero or one.
Dirac's Thermodynamic Model
SWUs are a function of the concentrations of the feedstock, the enriched output, and the depleted tailings.
The work necessary to separate a mass of feed of assay into a mass of product assay , and tails of mass and assay is given by the expression:[1]
where is the value function, defined as:[2]
The feed to product ratio is given by the expression
whereas the tails to product ratio is given by the expression