Pythagorean theorem
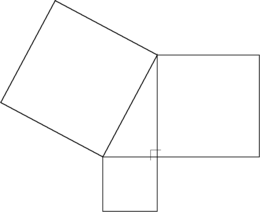
In Euclidean geometry, the Pythagorean theorem states that:
- The sum of the areas of the squares on the legs of a right triangle is equal to the area of the square on the hypotenuse.
The "legs" are the two sides of the triangle that meet at a right angle. The hypotenuse is the other side—the side opposite the right angle.
The Pythagorean theorem is commonly known by its algebraic notation:
a² + b² = c²
where a and b are the lengths of the two legs of the right triangle and c is the length of the hypotenuse.
Proof of the Pythagorean Theorem
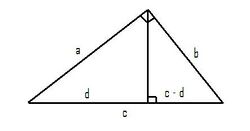
Take a right triangle with legs of length a and b and hypotenuse of length c. Draw a line from the right angle perpendicular to the hypotenuse dividing the hypotenuse into segments of length d and c - d as pictured.
This line divides the triangle into two smaller triangles, both of which are similar to the original triangle. (This is evident by the fact that both of these new triangles are right triangles and share a second angle with the original triangle.) Because these triangles are similar to the original triangle, the following proportions hold:
cross multiplying both equations gives:
a2 = cd
and
b2 = c(c - d) or b2 = c2 - cd
combining both equations gives:
a2 = cd
+
b2 = c2 - cd
a2 + b2 = c2