Legendre-Gauss Quadrature formula

Legendre-Gauss Quadratude formiula is the approximation of the integral

(1) $\int _{-1}^{1}f(x)\,dx\approx \sum _{i=1}^{N}w_{i}f(x_{i}).$

with special choice of nodes $x_{i}$ and weights $w_{i}$, characterised in that, if the finction $f$ is polynomial of order smallet than $2N$, then the exact equality takes place in equation (1).

Legendre-Gauss quadratude formula is special case of Gaussian quadratures of more general kind, which allow efficient approximation of a function with known asumptiotic behavior at the edges of the interval of integration.

Nodes and weights

Nodes $x_{i}$ in equation (1) are zeros of the Polynomial of Legendre $P_{N}$:

(2) $P_{N}(x_{i})=0$

(3) $-1<x_{1}<x_{2}<...<x_{N}<1$

Weight $w_{i}$ in equaiton (1) can be expressed with

(4) $w_{i}={\frac {2}{\left(1-x_{i}^{2}\right)(P'_{N}(x_{i}))^{2}}}$

There is no straightforward espression for the nodes $x_{i}$; they can be approximated with many decimal digits through only few iterations, solving numerically equation (2) with initial approach

(5) $x_{i}\approx \cos \left(\pi {\frac {1/2+i}{N}}\right)$

These formulas are described in the books

Example

Fig.1. Example of estimate of precision: Logarithm of residual versus number $N$ of terms in the right hand side of equation (1) for various integrands $f(x)$.

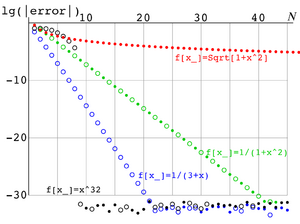
In Fig.1, the decimal logarithm of the modulus of the residual of the appdoximation of integral with Gaussian quadrature is shown versus number of terms in the sum, for four examples of the integrand.

$f(x)=x^{16}$ (black)

$f(x)={\sqrt {1+x^{2}}}$ (red)

$f(x)=1/(1+x^{2})$ (green)

$f(x)=1/(3+x)$ (blue)

The first of these functions is integrated "exactly" at $N>8$, and the residual is determined by the rounding errors at the long double arithmetic. The second function (red) has branch points at the end of the interval; therefore, the approximation does not improve quickly at the increase of number terms in the sum. The last two functions are analytic within the range of integration; the residual decreases exponentially, and the precision of evaluation of the integral is limited only by the rounding errors.

Extension to other interval

is straightforward. Should I copypast the obvious formulas here?