User talk:Paul Wormer/scratchbook

Proof

Differential equation

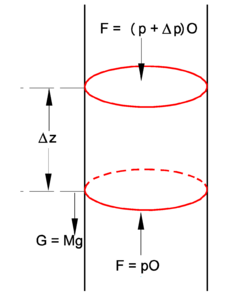
PD Image
A pillbox of height Δz and cross section O filled with air. Pillbox, with upward pressure p at its bottom, is part of a cylinder filled with air. Total mass M of air in pillbox is pulled downward by gravitational acceleration g'.

In the figure we see a stationary pillbox at arbitrary position z in a cylinder filled with air. The pillbox is pushed up by a pressure force pO, and pulled down by gravitation, which gives a force G equal to the total mass M of air in the pillbox times the gravitational acceleration g. Also the air pressure (p+ Δp)O at the top acts downward. Forces upward are positive, downward negative, and since the total force is zero (no motion of air), we have

$pO-Mg-(p+\Delta p)O=0\;\Longrightarrow \;\Delta p=-{\frac {Mg}{O}}$

The total mass in the pillbox is the molar density ρ times the molar mass m times the volume of the pillbox Δz·O

$M=\rho m\Delta zO.\;$

Hence

$\Delta p=-\rho mg\Delta z\,$

Noting that the molar density is the number of moles per volume, we get for an ideal gas,

$p=\rho RT\;\Longrightarrow \;\rho ={\frac {p}{RT}}$

Assuming that the gas in the pillbox is ideal and of absolute temperature T, we get the equation

$\Delta p=-p{\frac {mg}{RT}}\Delta z\;\Longrightarrow \;{\frac {1}{p}}{\frac {\Delta p}{\Delta z}}=-p{\frac {mg}{RT}}$

Taking the limit of infinitesimal small Δ and remembering that the derivative of the natural logarithm is given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{p(z)} \frac{dp(z)}{dz} = \frac{d\ln p(z)}{dz}, }

we arrive at the the differential equation

${\frac {d\ln \,p}{dz}}=-{\frac {mg}{RT}}.\qquad \qquad \qquad \qquad \qquad \qquad \qquad (1)$

Constant temperature

The master equation (1) can be solved by integrating the left hand side from p₀ to p and the right hand side from z₀ to z. Hence

$\ln {\frac {p}{p_{0}}}=-{\frac {mg}{RT}}(z-z_{0})\qquad \qquad \qquad \qquad \qquad (2)$

where we recall that

$\ln p-\ln p_{0}=\ln {\frac {p}{p_{0}}}$

Taking the exponent (the inverse function of the natural logarithm) of both sides of equation (2) we get

${\frac {p}{p_{0}}}={\frac {\exp \left[-{\frac {mg}{RT}}z\right]}{\exp \left[-{\frac {mg}{RT}}z_{0}\right]}}\;\Longleftrightarrow \;p=p_{0}\,\exp \left[-{\frac {mg}{RT}}(z-z_{0})\right]$

This distribution is known in statistical thermodynamics as a Boltzmann distribution.

Temperature linear in height

We assumed in the previous subsection that T is constant throughout the cylinder, which makes the equation useful for cases where there is no temperature gradient, i.e., case where the temperature at the top of the cylinder is equal to the temperature at the bottom. The master equation (1) can be modified for the case of a constant temperature gradient (constant lapse rate). That is, we make the substitution

$T\rightarrow T+K(z-z_{0})$

in equation (1). The modified equation is still easily integrated:

$\int _{p_{0}}^{p}d\ln \,p'=-{\frac {mg}{R}}\int _{z_{0}}^{z}{\frac {1}{T+K(z'-z_{0})}}dz'$

Substitute

$y=T+K(z'-z_{0})\;\Longrightarrow \;dz'={\frac {1}{K}}dy$

The integral on the right hand side becomes

$-{\frac {mg}{R}}\int _{z_{0}}^{z}{\frac {1}{T+K(z'-z_{0})}}dz'=-{\frac {mg}{KR}}\int _{T}^{T+K(z-z_{0})}{\frac {dy}{y}}=-{\frac {mg}{KR}}\ln {\frac {T+K(z-z_{0})}{T}}=\ln \;\left[{\frac {T}{T+K(z-z_{0})}}\right]^{\frac {mg}{KR}}$

We already saw that the integral on the left hand side is the logarithm of p/p₀. hence

${\frac {p}{p_{0}}}=\left[{\frac {T}{T+K(z-z_{0})}}\right]^{\frac {mg}{KR}}.$