User:John R. Brews/Sample

{{TOC|right}

In the theory of electrical circuits, Thévenin's theorem allows the replacement of a two-terminal portion of a linear circuit by a simplified circuit consisting of a voltage source, called the Thévenin voltage source, in series with an impedance, called the Thévenin impedance. Thévenin's theorem is the dual of Norton's theorem, which replaces a two-terminal portion of a linear circuit by a simplified circuit consisting of a current source in parallel with an impedance.

Finding the Thévenin components

To determine the Thévenin voltage, open circuit the two terminals and measure or calculate the open-circuit voltage across the terminals.

To determine the Thévenin impedance, set all independent sources between the two terminals (leave the dependent sources active), and determine the impedance seen looking into the two terminals. For example, apply a known voltage across the terminals and measure the current drawn, or apply a known current and determine the voltage developed. The Thévenin impedance is then the ratio of the voltage across the terminals to the current passing through the terminals.

In the case of a frequency dependent applied voltage or current, the impedance may be dependent upon frequency and exhibit a phase dependent upon frequency, as normally expressed using an impedance represented by a complex number.

Example

(PD) Image: John R. Brews
Bipolar buffer amplifier.

(PD) Image: John R, Brews
Small-signal circuit for voltage follower.

(PD) Image: John R. Brews
Determination of the small-signal output resistance. R_E=R_L//r_O.

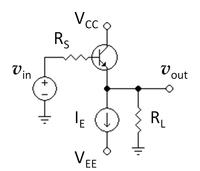
The bipolar circuit in the figure at left represents a voltage buffer. The operation of this circuit is as follows. The DC current source I_E determines the current leaving the emitter in the quiescent state when no signal is applied. By appropriate selection of the DC current source it can be arranged that the transistor is configured to operate usefully, that is, it is in active mode.

A signal voltage v_in is applied to the base. The emitter-to-base voltage of the transistor is hardly affected by the signal, and remains very nearly at the quiescent value determined by the bias current I_E. Consequently as the signal changes the base voltage, the emitter voltage follows suit, and the output signal v_out is a copy of the input signal v_in. The DC current source does not permit any time varying current to pass through it, so at the signal frequency it behaves as an open circuit.

As this discussion indicates, the voltage gain of this circuit is very nearly unity, so amplification is not achieved. The purpose of this circuit is to isolate the signal source from the load R_L, with the object of preventing the load from affecting the performance of the source. In particular, if the source is forced to draw a large current, that may adversely impact its performance, and this circuit insures that only a small current is demanded of the source. This circuit therefore is called a voltage buffer.

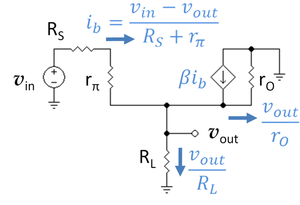
The transistor is a very nonlinear device, so the output signal voltage across the load resistor is not a faithful amplification of the input signal at the base unless the signal amplitude is small. For purposes of estimating the amplifier behavior, the assumption is made that the signal amplitudes are very small so the amplifier appears to behave as a linear circuit. Under these circumstances, the transistor can be approximated by a linear circuit composed of resistors called the hybrid pi model. The linear small signal approximation to the circuit using the transistor hybrid pi model is shown in the figure with a few algebraic expressions derived by application of Ohm's law. This circuit is used to determine the Thévenin voltage (the open circuit voltage) of the buffer.

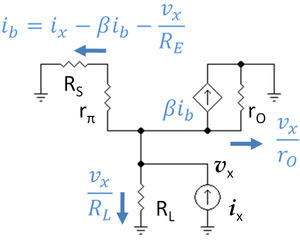
To apply Thévenin's theorem, the resistance of the circuit looking back into the circuit from the output nodes is needed. That is accomplished using the second small-signal circuit. To determine the Thévenin impedance, the signal source is set to zero (short-circuited) and a test current I_x is applied to the output and the resulting voltage at the output V_x is determined.

To apply this program, Kirchoff's current law is applied to the emitter node in the upper small-signal circuit to obtain:

${\frac {v_{out}}{v_{in}}}={\frac {{\frac {1}{R_{L}}}+{\frac {1}{r_{o}}}+{\frac {\beta }{R_{S}+r_{\pi }}}}{\frac {\beta +1}{R_{S}+r_{\pi }}}}\approx {\frac {\beta }{\beta +1}}\ .$

Of course, the load resistor R_L should be allowed to become infinite to obtain an open-circuit condition, and the transistor output resistance is very large. Hence the validity of the approximate form.