Systems biology

As an academic discipline, systems biology aims to explain, predict and control the properties, functions and behaviors of biological systems — complex assemblages of interrelated, dynamically interacting, coordinated and hierarchically organized naturally selected components generated over evolutionary time by natural biochemical and biological experiments.  Biological systems studied range from the level of the molecular subsystems of cells (e.g., usable energy production by mitochondria; circuits regulating gene expression; cell-to-cell and within-cell signaling (communicational) pathways) to Earth's biosphere, and include a large number of intermediate system levels (e.g., unicellular organisms, multicellular organisms, ecosystems).

Systems biologists try to achieve their aims in part through developing models (descriptions, representations, simulations) of systems — various kinds kinds of models, including graphical, mathematical and computer-based simulation models. The models aspire to 'describe' systems, or 'translate' them into the known 'language' of the model, to enable interpretation of the systems' components' interrelations by human cognition. The models aspire to do that sufficiently well to account for experimentally derived data about a system’s interacting components, and allow predictions of the system's properties, functions and behaviors in response to given stimuli or given sets of conditions. Systems biologists use sophisticated mathematical, statistical and computational tools in diverse modeling approaches, in mathematical network analyses, in computer simulations, in design and building synthetic networks from biomolecules, and, iteratively, incorporating new data derived from systems-analysis-inspired further experimentation.

Modeling permits a kind of formal integrative analysis of a biological system that also enables the development of conceptual frameworks to integrate large amounts of data and identify gaps in the information known about a system. Without models, the human mind can comprehend little of the organization as a whole of a complex living system. In speaking specifically about cellular signaling pathways, Weng et al. put it this way: There is simply too much essential detail in biological signaling for the unaided human mind to organize and understand.

Systems biologists often work with non-biological scientists, from a variety of disciplines, in developing models and conceptual frameworks. No definition or succinct description can capture the breadth and depth of the interdisciplinary enterprise of systems biology. Indeed, historian and philosopher of science Evelyn Fox Keller argues that “so far, ‘systems biology’ is a concept waiting for definition".  This article elaborates on the above description of the discipline.

Methodologies in general terms

Systems biologists try to accomplish their aims in part:

• by identifying and quantifying the system's components — for cells, acquiring so-called '-omics' data, including the numbers and types of nucleic acids, proteins, and metabolites;

• by identifying, characterizing, and to the extent possible, quantifying the interrelations (structural) and interactions (dynamical, coordinated, hierarchical) among the components of a system; for example, (a) molecular components: gene and protein interactions involved in a cell’s metabolic pathways; (b) organism components: organ interactions resulting in blood pressure homeostasis; ecosystem components: predator and prey behaviors;

• by attempting to organize the system’s components abstractly in the form of 'models'/'simulations' — often mathematical and computational — which encode such concepts as 'modules', 'circuits' and 'networks', 'network motifs', 'feedback' and 'feedforward' loops, 'homeostasis', hierarchies, 'robustness, 'complexity', 'adaptation', and 'emergence';

• by conducting additional experiments to define interrelations and interactions of the real system that the model/simulation highlighted as knowledge gaps;

• by refining the model/simulation on the basis of the data from those experiments;

• by designing, constructing and testing synthetic networks from biological components.

For some systems, modeling may require the use of multiple datasets distributed in cyberspace, more than one mathematical or computational methodology, and even an array of interlinked computers having different architectures.

Systems biologists expect progress in the field to yield explanations of biological systems suitable for applications in ecology, ethology, medicine, agriculture, business, the environment and technology — and to a considerable extent it has already done so. Some systems biologists consider the discipline critical to further progress in biology.

The study of biological systems has expanded greatly as the result of major advances in molecular biology in the late 20th and early 21st century. Those include sequencing of genomes, developments in genetic engineering, and developments of technologies for generating massive amounts of data on the structure and interactions of cellular components---all fueled by increasing interest by non-biological scientists (mathematicians, statisticians, bioinformaticians, computer scientists, physicists, chemists, and engineers, among others) in applying the principles and methods of their disciplines to the explanation of the improbable adaptive complexity of living systems (see Figure 1).

On the nature of biological "systems"

A 'system' in biology is any interconnected, interacting, coordinated and hierarchical assembly of biological components or elements—an organized assemblage with an identifiable function. For example, the vertebrate body is an assembly of diverse, interacting organs, among other components, functioning to survive and reproduce. See other examples below. Each component in a biological system interacts in some way(s) with one or more components in the system--a dynamical assembly of components. For example, in the system constituting a cell, proteins are the products of genes, but they also interact with genes, affecting their expression, as well as with other proteins. Systems can exhibit behaviors that are characteristic of the system-as-a-whole (see below), but which are not shared by any of its components (so-called emergent behaviors). A tree fruits, for example, because its dynamically interacting components enable it to, but no single component of a tree can. (More on emergent behavior below.)

Subsystems consist of smaller (less complex) systems embedded in a larger (more complex) system, and constitute at least part of the components or elements of the larger system. Whether a systems biologist treats a given assembly of components as a subsystem or as a system depends on the 'level' at which she focuses her attention. If she focuses her research at the level of a whole vertebrate organism, for example, she treats its organs as subsystems. If she focuses her research at the level of the heart, she treats the heart's interacting components as a system, while recognizing that the heart remains a component or element of a larger system (the circulatory system).

Even the larger systems, such as the vertebrate body system, are components or elements of even larger systems, a species of vertebrates, say, where individual members of the species interact with each other, as components, to generate a set of behaviors or properties characteristic of the species but not of the individual members of the species. The flocking behavior of birds illustrates a species behavior--technically the behavior of a deme. One bird cannot flock.

When trying to understand biological systems, systems biologists need not treat the components or elements of a system (or subsystem) exclusively as discrete or concrete objects or entities (e.g., molecules, organelles, cells, etc.), but may also treat them as abstracted concepts of organizational collections or activity patterns of those objects or entities, admitting of study by mathematical, computational and statistical tools. Those include such concepts as circuits, networks and modules, more about which will follow below. Such concepts have a way of appearing less abstract or hypothetical as biologists more fully define them in terms of structure and coordinated dynamical interactions; predict systems behavior from them using quantitative models; and relate them functionally in the larger systems embedding them.

Biological system behaviors typically perform one or more evolution-informed functions (e.g., growth), so unravelling the evolutionary history of a biological system contributes importantly in fully explaining it.

Examples of biological systems (subsystems) include:

• the biosphere
• ecosystems (e.g., a forest)
• demes (e.g., a local population of a species)
• organisms (e.g., humans; bacteria)
• organs (e.g., brain; the vascular endothelium)
• cells (e.g., epithelial cell)
• metabolic pathways (e.g., glycolysis)
• cellular organelles (e.g., mitochondria)
• genomes (e.g., the entire complement of DNA in an organism, as the ’mouse genome')
• gene complexes (e.g., co-expressing genes)
• genes (e.g., protein blueprints)
  

History of systems biology

Knowing the historical path(s) that led to a modern scientific program can help in understanding the nature of the program, in particular, its goals and its methodologies, especially through considering the different focuses and approaches that different historians have taken when writing about the same topic.

The evolution of molecular biology into systems biology

Westerhoff and Palsson introduce the school of thought “…that systems biology of the living cell has its origin in the expansion of molecular biology to genome-wide analyses.” They point out, however, that molecular biology has an earlier history of systems thinking, in particular in the elucidation of the many molecular regulatory circuits and of their contribution to the logic of the cell. They see technological advances that have permitted rapid collection of large data sets (so-called high-throughput technologies mapping the genome) as upping the scale of that research “…enabling us [molecular biologists] to view the genome as the ‘system’ to study.”

They describe two pathways of enquiry that they see as having merged into modern systems biology of the cell.

One root is the advances in molecular biology that ultimately “…led to efforts toward genome-scale model building to analyze the systems properties of cellular function”: recognition of DNA as the genetic material, identifying the structure of DNA, recombinant technology, automated determination of DNA base sequences, and high-throughput technologies yielding the sequences of entire genomes.

A second, parallel root is the development of non-equilibrium thermodynamics, a predictive mathematical theory for describing the behavior of systems that transfer energy from one place to another or convert energy from one form to another in processes the move towards an irreversible state of stability characterized by randomness or disorder—for biological systems, death. Because living systems produce order and maintain a state of non-randomness, they must carry out processes that keep them in a condition far from the equilibrium of randomness, and they achieve this by transforming energy (and matter and information) taken in from the environment. The non-closed biological system produces order at the expense of the environment it opens to, while the environment becomes more disordered.

Westerhoff and Palsson describe advances in the development of non-equilibrium thermodynamics as presaging molecular and cellular systems biology through ‘quantitative’ integration of system components and through the discovery of principles connecting molecular mechanisms and system behaviors. Westerhoff and Alberghina ask of systems biology: “Did we know it all along?”

Historical milestones in the development of systems biology

Anthony Trewavas, a scientist conducting research in the molecular and systems biology of plant cells, emphasizes the following aspects of the history of systems biology:

• How Rene Descartes’ formulation of reductionism—the concept that the properties of complex objects can be explained by reducing them into their parts and studying the properties of the parts —led biologists to assume that one could explain a complex biological system's behavior from the behavior of its subsystems;

• How reductionism played hand-in-hand with the mechanistic view of reality, leading biologists to view systems as predetermined machines, like clocks;

• How reaction against the reductionist-mechanistic view led to a holistic view of biological systems consistent with Aristotle’s dictum, commonly expressed as "the whole is greater than the sum of its parts";

• Aristotle qualifies as a "systems biologist" as he viewed the behavior of a complex living system as finally explaining (final cause) why the system has the parts (material cause) interrelated (formal cause) and interacting coordinately (efficient cause) that it does;

• How experiments revealed that the averaged behavior of a population did not apply to individual members of the population, however homogeneous the population appeared, complementing experiments revealing non-machine-like toleration of large variability among kindred organisms, organs and cells with respect to behavior and function—each manifesting a so-called norm of reaction that overlapped among individuals;

• How a system’s organization of subsystems itself exerts a level of control and constraint over the range of behaviors available to the subsystems in isolation;

• How a system’s subsystems are organised in hierarchies, where the properties of a subsystem emerge from the dynamic interactions of subsystems at lower levels of the hierarchy;

• How subsystems at lower levels of hierarchy exhibit more variability and how their behavior exhibits more order within the system than without—the higher level emergent properties orchestrate and constrain the behavior of the subsystems generating that emergence;

• How Karl Ludwig von Bertalanffy (1901-1972) recognized that all systems share “…the common property of being composed of interlinked components, in which case they might share similarities in detailed structure and control design”;

• How Michael Polyani (1891-1976) recognized that adjacent levels of a system’s subsystems constrain each other and that upper level behaviors require the lower level behaviors;

• How psychologist and polymath Donald T. Campbell (1916-1996) coined the term “downward causation” to describe higher system level constraints on lower levels, as in constraints on gene expression by higher level subsystems—a prelude to understanding ‘emergent’ systems as having properties or behaviors that “make a difference”, i.e., have causal properties;

• How Claude Bernard, Walter Cannon, and Norbert Weiner established the importance of negative feedback for maintaining stability within large systems, leading to subsequent demonstration of negative feedback at the molecular level;

• How the identification of feed-forward mechanisms led to advances in understanding the features characterizing the design of systems control mechanisms.

Growth of publications relating systems biology

Figure 1. Growth in papers on systems biology.

The pace of research in systems biology greatly accelerated at the beginning of the 21st century.

The figure at left shows the exponential growth of publications relating to or discussing systems biology from 1996 to 2006.

The data come from the National Library of Medicine's PubMed database, and probably underestimate annual "systems biology" publication rates by not including articles in journals in many non-biological disciplines.

Early systems modelers

In 1952, the British neurophysiologists and nobel prize winners Alan Lloyd Hodgkin and Andrew Fielding Huxley constructed a mathematical model of the action potential - the fundamental mechanism underlying communication between nerve cells, expressing it as the consequence of a dynamic interaction between interdependent ionic conductances of the cell membrane. In 1960, Denis Noble developed the first computer model of a beating heart. Systems biologists invoke these pioneering pieces of work as illustrative of the systems biology project.

Systems biology as an evolutionary trend of classical integrative physiology

In the view of physiologists and bioengineers Daniel A. Beard and Marko Vendelin, the term 'systems biology' and 'physiology' synonymize, as they argue:

"In a nutshell, "systems biology" attempts to realize this [its] promise by measuring and mapping biological interactions within cells, tissues, organs, and organ systems, and predicting how integrated systems made up of many interacting components behave. Readers of the American Journal of Physiology may wish to point out that by such a definition, the term "systems biology" is essentially a synonym for "physiology." While we would not argue with that assessment, we suggest that the increasing attention being paid to the endeavor is at least in part due to the injection of a new term, and associated new techniques and technologies, into the well-established field of integrative physiology. It has been argued that this increase in attention places the discipline of physiology in a position where it will either be "superseded...by systems biology" or will enjoy a renaissance as it leads the way in research in this area..."

Molecular physiologist and biophysicist Kevin Strange earlier made the comparison:

”Physiology and systems biology share the goal of understanding the integrated function of complex, multicomponent biological systems ranging from interacting proteins that carry out specific tasks to whole organisms."

In writing of systems biology, Strange encourages 21st century physiology departments “to embrace them as essential components” of their field, by ‘them’ referring specifically to “functional genomics, nonmammalian model organisms and computational biology”. He sees a ‘critical mass’-type advantage to a diverse group of physiologists and post-genomics-brand systems biologists working as a group.

Marine biologist, John Bothwell, “…argue[s] that systems biology…retreads the conceptual ground covered by post-Darwinian physiology and resembles nothing more than the application of 19th century physiological reasoning to today’s molecular biological data.” He credits systems biologists for their focus on developing mathematical methodologies for the study of complex cellular networks.

Many others have likened physiology and systems biology. Certainly physiology dates to the beginnings of biology as a discipline, and systems biology dates even to Aristotle. The process of homeostasis, of particular interest to systems biologists, has a long history in physiological studies. In the 19th century, the French physiologist, Claude Bernard, who developed the concept of the ‘internal milieu’, or ‘internal environment’ (e.g., for maintaining blood composition), performed experiments showing animals maintaining their internal milieu within favorable limits—essentially recognizing the process of homeostasis. The early 20th century physiologist Walter Cannon introduced the term 'homeostasis' and demonstrated the homeostatic role of the autonomic nervous system. Physiologists continue to study the mechanisms of homeostasis in systems throughout the body, publishing in the American Journal of Physiology journal suite (excluding cell and molecular physiology journals) 43 papers on the subject in 2005 and 2006, the titles of which appear in Appendix A.

Perhaps someone will write an integrated article combining the 'History of Physiology' and 'History of Systems Biology'. Constraints on prolixity discourage further development of issues pertaining to the relation of physiology and systems biology in this article.

Modeling in systems biology

For systems biologists, modeling serves as the key to unlocking the system of interest, whether a cell, a species, or an ecosystem.

Reminding us of the story of the six blind men investigating a different part of an elephant and coming up with six different descriptions of the animal, James Haefner wrote:

One failure of the blind men was to ignore the relations between objects. A seventh man, one sensitive to the importance of testing alternative models, might have said: “Hmmm, ‘tree’, ‘snake’, ‘fan’, ‘spear’, ‘wall’, ‘rope’: It’s a single, big thing with columnar supports and appendages at the ends.” The blind men, especially, need a systems approach, and with respect to the scientific unknown, we are all blind.

To understand a key systems approach, one must know something about model building, or simply, modeling. Models represent (re-present) reality in an abstract form, such as a narrative description (e.g., a theory, conceptualization, rule), a diagrammatic representation (e.g., a graph or network diagram), a physical representation (e.g., a scale model), a 'formal' representation (a mathematical or quantitative description), and simulation models. Most simulation models entail numerical approximations of sets of mathematical expressions potentially describing the system, and ‘stepping-through-time’ with imposed value changes in the states of the system — typically through computer-based computational processing.

Systems biologists use numerous different diagrammatic and mathematical models as keys to understanding biological systems — their logic, say — as keys to explaining, predicting and controlling their behavior.

Mathematical models of a biological system employs sets of equations in describing the system. They posit a series of mathematical expressions (equations) to describe the activity of the system, they comprise analysis of the system by mathematical relations without resort to numerical approximation, and may have dynamic properties by describing the activity of the system over time. They can serve these main functions:

• They allow management of data sets of structures and interactions too large and complex for the human mind to manage without the “exo-cortex” of mathematical formulations, often computer-based for quantitative outputs;

• They allow an iterative process whereby experimental data about a system inspires the model, and the output of the model reveals the need for further experimental research, the results of the latter inspiring changes in the model, which repeats the cycle as the output of the model approaches the realities of the system;

• By failing to fully account for the targeted behavior of the system:

• they raise the possibility of the existence of unknown subsystems of the system that require further experimental work, and may give direction to that further research;

• they inspire refinements of the model to account for the gaps;

• They provide an satisfying and usable ‘explanation’ of the system—an explanation of its properties, functions and behaviors in quantitative terms of its coordinated, dynamically interacting, hierarchically arranged components;

• They enable ‘control’ of the system—the ability to induce a desired behavior or propensity with the appropriate manipulation;

• They enable ‘prediction’ of the behavior of the system—predicting how it will respond to a given set of circumstances, especially predicting novel behaviors of the system.

Despite the large datasets available for many biological systems, especially cell systems, they still fall short in quantity and quality for realizing the full potential of quantitative modeling in applying advanced methodologies for statistical analyses, testing of hypotheses, and estimating the values of equation constants and independent variables. Wellstead et al. note the “enormous challenges to bio-sensing for systems biology” that lie ahead.

Harvard biomathematician and philosopher of science, Richard Levins, speaks to the value of mathematical modeling:

Mathematics is used mostly in modeling in order to predict the outcomes of systems of equations. But it also has another use: educating the intuition so that the obscure becomes obvious. When we abstract from the reality of interest to create mathematical objects, we do this because some questions which would seem intractable now can be grasped immediately. We can look at the fluctuating abundance of insects and conclude ‘‘since these bugs vary by several orders of magnitude during the year and yet remain within bounds from year to year, there must be some density dependence operating (a negative feedback),’’ or see that in a particular patient insulin seems to increase blood sugar and we have to ask, ‘‘where is there a positive feedback loop at work?’’ This kind of qualitative mathematics is essential so that we are not overwhelmed by the sheer numbers of equations and variables of predictive models. The teaching of mathematics to scientists must include the mathematics that aims at understanding rather than solving equations or projecting numbers.

Haefner has provided a classification of mathematical models based on whether the mathematics explicitly represent (a) the mechanisms of the processes of interest, (b) the future states of the system, (c) time as continuous, (d) spatial aspects of the systems, and (e) the effects of random events. Yes/no answers correspond to mathematical structures yielding (a) mechanistic/descriptive models, (b) dynamic/static models, (c)continuous/discrete models, (d) heterogenous/homogenous models of space, and (e) stochastic (random)/deterministic models. A given model might incorporate mathematical structures of any combination of (a) through (e).

Some examples of familiar models

The examples below facilitate learning about modeling heuristically.

A road map of an urban complex

Courtesy flickr.com by "entro_py" at http://www.flickr.com/photo_zoom.gne?id=36231753&size=l&context=datetaken

For a given level of detail, a road map represents (re-presents, or models) the structure of the system of roads in a region of land at a given point in time, using the language of graphic illustration. In network parlance, cities and other points of interest (e.g., parks, lakes) serve as nodes and the connections between nodes serve as edges, some of which may indicate one-way connections only. Using the road map, one can control the system of roads in the sense that one can exploit the information to get from one place (node) to another, and predict how long it will take to get there.

The level of detail in a roadmap may not allow determination of the grades of the roads (steepness) or the degrees of curviness or the position of side roads or new roads added since the date of the map.

Systems biologists use maps, for example, to model the structure and interrelationships among biochemical molecules in cellular subsystems, such as the subsystems that convert glucose to usable energy and to other biochemical molecules (e.g., glycogen).

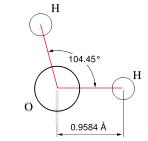
A chemical formula

Figure 2. Atomic dimensions of a water molecule.

Anyone reading this far knows H2O as a model (representation) for the substance, water. As such it has many uses, in particular in modeling chemical reactions. Other models of water, such as HOH, provide additional information for particular purposes. Note that the model does not give any indication of the 'emedrgent' properties of liquid water, say, or of water ice or steam.

A computer-based flight simulator

For a given level of detail, a computer-based flight simulator represents the multi-subsystem of a flight vehicle system (e.g., airplane), including its control characteristics, and the environment in which the flight vehicle must interact with in order to function stably and exhibit its system behavior of taking off, flying to destination, and landing. The representation (model) uses the languages of engineering, mathematics, computer programs, and dynamical graphics, among others to enable control of the system and to predict its behavior in response to a given set of environmental conditions for comparison with the response to those conditions in real flight—testing the goodness of fit of the model.

Systems biologists use computer-based simulators, for example, to predict the behavior of the human heart in response to drugs.

Newton’s equations

For macroscopic mechanical systems, Newton’s equations represent, or model, the behavior of bodies of mass in motion, allowing predictions of the trajectories of moving masses, including the masses comprising the solar system; allowing calculation of the strength of the mutual attraction of masses and the contribution of each of two masses to that attraction; enabling explanation of macroscopic properties of gases and liquids (e.g., pressure, temperature) from the average effects of microscopic particles interacting in conformity with Newton’s equations; and, enabling engineers to construct vehicles for transporting humans to the moon and back.

(Erwin Schrodinger's wave equation does for subatomic mechanics what Newton's equations did for macroscopic mechanics, and Albert Einstein's General Relativity theory explained away Newton's action at a distance--as models advance in capability.)

Systems biologists use mathematical expressions, often more complex than Newton’s equations, based on empirical data and theoretical principles, in numerous ways to model the behavior of biological systems at all hierarchical levels. See below.

Examples of modeling in systems biology

Introductory remarks here…

Darwin’s theory of evolution by means of natural and sexual selection

Darwin’s theory, stated conceptually in words, and its 20th century amplification, stated genetically/molecularly often in quantitative terms, represents, or models, the behavior of nature in creating species and varieties sufficiently adapted to their environment to survive long enough to reproduce and care for their offspring and kin. The theory enables understanding of an enormous range of behaviors of animals, plants, unicellular organisms, and cellular and subcellular systems, and has explanatory and predictive value in every biological discipline, and many non-biological disciplines.

Evolutionary principles permeate the discipline of systems biology and have led to the emerging discipline of “evolutionary system biology” A case in point: Determining whether natural selection operating at the molecular level has forged the structure of molecular networks may enhance understanding of their underlying design principles and thereby facilitate design of better predictive models.

Bipedal and Quadrupedal Walking and Running'

In the human organism, walking and running emerge as system behaviors (no subsystem itself walks or runs). The energy cost to the system of those locomotor behaviors defines a property of the system applicable to those behaviors. The energy cost owes to the appropriate forces the system must generate to support itself against gravity and to swing the locomoting limbs to achieve forward motion. Researchers have found that the rate at which the system produces those forces—shorthanded simply to ‘force production’—correlates with the system’s energy cost of locomotion. Thus, if one could develop a mathematical model that predicts force production from readily determined values of variables related to anatomy (e.g., limb length) and motion (e.g., forward speed), that model could then predict the system property of energy cost of locomotion.

Based on the findings of earlier studies, Harvard anthropologist Herman Pontzer developed a mathematical model—viz., an equation—that justified force production as a function of three variables: the rate of muscular force production in the vertical direction, the rate of muscular force production in the horizontal direction, and the rate of muscular force production required to swing the limbs. From empirical data, knowledge of trigonometry and physics (force mechanics) and of muscle physiology, he identified measureable anatomical and motor variables--length and proportion of limbs, speed, frequency of stride, and angle of excursion--that allowed estimation of those required three force variables. Following earlier studies that linked force production with cost of locomotion, he generated the model--the equation--that he hoped would predict the latter from the former. He found that the model well predicted the observed cost of locomotion, somewhat better for running than walking.

Subsequently, Professor Pontzer tested the model in quadrupeds as well as humans. The model proved superior to previous models, extending it to quadrupeds, and confirming the predictive ability of considering the proposed anatomical variables in estimating the rate of force production and energy cost of locomotion.

With the development of quadruped and biped robots for human service, Professor Pontzer's model might help make decisions on energy-cost-effective robot locomotor anatomy and dynamics.

Modeling Noise-Effects on Biochemical Processes and Cell Systems Behavior

Randomness can influence the rate that a gene 'expresses' production of its encoded protein, for example, through random effects on the rate of DNA’s replication as messenger RNA. Biologists refer to that as noise in the gene expression ‘molecular-machine’—fluctuations in expression rate (‘machine output’). A protein repressor of DNA for producing messenger RNA might have a low number of molecules available for the binding to the DNA that effects the repression. In that case, the total time of bound repressor-DNA will vary because of the random nature of molecules diffusing in a solution, which will also affect the time-pattern of messenger RNA production (how often and how long each time). With fewer repressor molecules, random diffusion effects can dictate how rapidly repressor rebinds after diffusing off the DNA, and thereby can influence the total time DNA remains unrepressed and the time-pattern absent repression. Because binding requires two molecules approaching, the spatial distribution of the low numbers of repressor molecules affected by the randomness of its diffusion patterns can produce fluctuating bursts of gene expression---noise.

van Zon and colleagues developed a mathematical model to explain repressor-number-related noise in gene expression based on physical principles and statistical analyses of randomness based on probability theory. They show that their model, with its simplifying assumptions, predicts burst-expression found experimentally, but they admit that the model does not allow for the more complicated effects of random diffusion in cell systems.

van Zon et al. point out that such noise in gene expression as in their model could have significant effects on cellular function, giving specific examples. On that issue, Samilov et al., in their review of the ‘physiology of noise’, point out that “fluctuations in random biomolecular interactions” [noise] can lead to differences in the behavior of otherwise identical cells (clones) that enable the cells' tissue/organ more choices of adaptive response to environmental changes than a purely noise-free system would have. Noise in biological machinery therefore can have positive effects. Paradigmatic of that, random mutation of gene composition enables evolution by means of natural selection.

Samilov et al. decribe other ways to model noise in biological systems. Rao et al. reference many different modeling approaches to explore the control, rejection, elimination and exploitation of noise, and extensively highlight reasons we need to explain the role of noise in biological systems.

Simulation modeling of an avian influenza pandemic in the United States

To consider the effects of an avian influenza outbreak in the U.S., workers at the Los Alamos National Laboratory, the Fred Hutchinson Cancer Research Center and the School of Public Health and Community Medicine at the University of Washington in Seattle,  using a supercomputer and specialized software, simulated the spread of a pandemic influenza viral strain through an artificial U.S. population (281 million people). To perform the simulation, they generated a model with realistic assumptions of transmissibility values, and considered the effect of variable antiviral and vaccine use, and of different modifications of social mobility (e.g., travel restrictions). They describe the basics of their model:

The three basic elements of our national-level simulation model are (i) a previously developed stochastic agent-based model for disease spread at the community level; (ii) detailed U.S. Census demographics and worker flow data for daily commuter traffic at short distances and Bureau of Transportation Statistics data for less frequent long-range travel behavior; and (iii) high-performance parallel computing expertise in modeling millions to billions of particles on hundreds to thousands of processors.

Modeling the mitochondrion

Vo and Palsson reviewed the advances systems biology research has made in explaining the integrated workings of the complex cellular subsystem, the mitochondrion—the cell’s transformer of the external matter and energy taken up by the cell into a usable cellular energy-currency:

”With the rapidly increasing number of discovered molecular components [of mitochondria], computational models are also being developed to facilitate the organization and analysis of such data. Computational models of mitochondria have been accomplished with top-down [starting with a theoretical model of the system then tested against the data] and bottom-up [starting with the data and building up to the model] approaches and have been steadily improved in size and scope. Results from top-down methods tend to be more qualitative but are unbiased by prior knowledge about the system. Bottom-up methods often require the incorporation of a large amount of existing data but provide more rigorous and quantitative information, which can be used as hypotheses for subsequent experimental studies.”

To cite one example: Using massive data sets on mitochondrial components and chemical reactions, combined with mathematical assumptions and computer-based mathematical analyse, Vo et al. ‘constructed’ (aka modeled) a network of biochemical pathways that preserved the known interactions among the components. The constructed networked described mitochondrial energy production and other mitochondrial functions closely in accord with experimental results.

The authors recognized the need for more experimental data of mitochondrial components and function to refine the model for predictability.

Modeling by Engineering Synthetic Systems

Systems biologists model systems also by using advanced and innovative experimental techniques to construct synthetic versions of a system with real system elements. They propose a design blueprint for the synthetic system based on empirical data about the system and the results of mathematical and computational tools used to analyze that data. With appropriate designs or tags, they can then observe and analyze the behavior of the synthetic system, in effect viewing it in isolation from the larger system embedding it. That potentially leads to insights into ways of manipulating the system for desired ends, including inducing novel behaviors of the system and the larger system embedding it.

[...specific examples of synthetic systems here...]

Multi-Level Modeling of the Heart

[...describe work of Denis Noble and colleagues..]

[...Work in progress…More examples to come...]

Emergent properties as ‘materialistic vitalism’

Some cell biologists might find it tempting to see a type of 'vitalism', or 'life force', in living systems, in view of the concept that some high-level features of organisms, including even the activity of living itself, exemplify emergent phenomena — phenomena not explainable after exhaustively studying the properties of each of the chemical processes that occur in the cell in isolation from the organization of the cell system embedding it. One could not explain, for example, the action of an organism fleeing from a predator from a study of the properties of an organism's component subsystems. The properties of the component parts depend on the organization of those parts in the whole system. . Because biologists and their co-scientists can explain emergent properties/phenomena, if only sometimes in principle, by mechanisms that do not transcend interactions of matter and energy, any such ‘vitalism’ properly qualifies only as a ‘materialistic vitalism’.

One example of emergence: When components of signaling pathways, which allow within-cell and between-cell communication, interact to form signaling networks, properties can emerge — such as self-sustaining feedback loops and generation of novel signals — that one cannot explain from the individuated properties of the separate pathways.

For another example, in studying a protein separated from the system it belongs to, one can observe many of its properties, but in so studying the protein one cannot observe any of the properties it has only in the context of the system that embeds it, such as the property of catalyzing a biochemical reaction, or of binding to other proteins to form a functional protein complex. Those properties of the protein emerge in the context of the protein’s environment — how it interacts in the system as a whole. Moreover, those emergent properties may result in effects within the system that, in a feedback way, further alters the properties of the protein in the system, as when a reaction product alters the catalytic properties of the protein.

Every biological system (e.g., a biochemical pathway) resides in a larger, more complex 'parent' system (e.g., an interconnected cycle with feedback) — essentially its environment — that has effects on the 'child' system. Those effects in turn can change the properties and behaviors of the 'child' system's subsystems that would not have existed without the system in its environment — a kind of 'downward causation'. Thus, in an environment of other birds of a feather, a system with flocking behavior may form that one can explain only by studying the behavior of the birds in the flocking-bird organization as a whole.

As Gilbert and Sarkar puts it: “Thus, when we try to explain how the whole system behaves, we have to talk about the context of the whole and cannot get away talking only about the parts.”

Emergent processes have been recognised as, for example, contributing to understanding:

• subcellular morphology ,
• developmental biology ,
• metabolic networks ,
• proteomics
• evolution of complexity in living things

Emergent phenomena appear even in non-biological physical systems.  Emergent phenomena attract the attention of cellular neuroscientists;  and cognitive scientists .  At still higher systems levels, emergent properties appear for example in the behaviour of ant colonies and the concept of swarm intelligence,  Artificial systems scientists have simulated emergent phenomena  Emergent phenomena in human societies has also received attention. .  Biologists even explain the biosphere itself as emergent.

We can elaborate on the principle that knowing the individuated properties of all the components of a system does not enable us to explain the properties of the system-as-a-whole — the opposite principle of the reductionist paradigm prevailing for centuries in physics and chemistry, and even in biology.   Firstly, the intrinsic properties of a system’s components do not of themselves allow description of the properties of the whole system, any more than a shoebox of Lego pieces disassembled from its erstwhile airplane reveal the finished product. Rather, the 'organizational dynamics' of the components explains the system, and those dynamics include not only the interrelations among the components themselves, but also interactions among the many different organizational units in the system. Secondly, the living system always operates in some context (its external environment, or surroundings), and that context, in turn, always affects the properties of the system-as-a-whole. For example, nutrient gradients influence the direction a bacterium’s locomotion. The impact of environmental context affects the organization of the components within the system — a 'downward causation'. For another example, environmental signals can activate or suppress a metabolic pathway, reorganizing cellular activity One cannot simply take a living system apart and predict how it will behave.

According to philosopher of science D.M. Walsh: "The constituent parts and processes of a living thing are related to the organism as a whole by a kind of 'reciprocal causation'." In other words, the organization of the components determine the behavior of the system, but that organization arises from more than the set of its internal components. How the whole system behaves as it interacts with its environment determines how those components organize themselves, and so novel properties of the system 'emerge' that characterize neither the environment nor that set of internal components.

For example, the behavior of a human kidney cell depends not only on its cellular physiology, but also on all the properties of the organ (kidney) which constitutes its environment. The kidney's overall structure and function influence the cell’s structure and behavior (e.g., by physical confinement and by cell-to-cell signaling), which in turn influence the organization of its intracellular components. The kidney in turn responds to its environment, namely the organism that it lives in, and that organism responds to its environment, which includes such factors as the availability of particular food items, fresh water, and ambient temperature and humidity.

Systems biologists thus regard emergent properties as arising from from a combination of bottom-up and top-down effects — Walsh's 'reciprocal causation'.

Other basic concepts that systems biologists consider crucial in explaining living systems as-a-whole include 'robustness', 'modularity', and 'networks' — all discussed in sections below. Quantitative modeling and simulation guided by experimental biological data provide the mainstay methodologies of systems biologists.

Emergent systems always display what we recognize as ‘complexity’, a feature we have a difficult time precisely defining. Complex systems appear to require more bits of information (words, sentences, lines of computer code, etc.) to describe than the bits of information in the system itself.  The operation of the system itself supplies its own most economical model.

According the paleontologist and origin of life researcher, Robert Hazen, four basic complexity elements underpin emergence in a system:

• a sufficiently large ‘density’ of components, with increasing complexity as the concentration increases, up to a point;

• sufficient interconnectivity of the components, with increasing complexity with greater and more varied types of interconnectivity, up to a point;

• a sufficient energy flow through the system to enable the system’s components to perform the work of interacting in the self-organized way characteristic of the energized system;

• flow of energy through the system in a cyclic manner, presumably facilitating the spatiotemporal patterning characteristic of organized systems.

References

NB: Some links to online full-text sources may require individual subscription to the online source, or access through an institutional subscription. Often the linked page contains at least a summary or abstract of the source if not the full-text.

Further reading, notes, and links

Books

• Alon U. (2007) An Introduction to Systems Biology: Design Principles of Biological Circuits. Boca Raton: Chapman and Hall/CRC ISBN 1-58488-642-0

301 pages; 12 chapters; 4 appendixes; 23 pages of references; glossary; Table of Contents

• Kaneko K. (2006) Life: An Introduction to Complex Systems Biology. Berlin: Springer ISBN 3-540-32666-9

370 pages; 12 chapters; 127 figures; 16 pages of references; Table of Contents

• Palsson B. (2006) Systems Biology - Properties of Reconstructed Networks. Cambridge University Press ISBN 9780521859035
• Szallasi Z, Stelling J, Periwal V (eds). (2006) System Modelling in Cellular Biology: From Concept to Nuts and Bolt. A Bradford Book, The MIT Press ISBN 0-262-19548-8

480 pages; 17 Chapters; 36 Contributors; Table of Contents and Full-Texts: Preface; Sample Chapter; Contributors; References

• Ellner SP, Guckenheimer J. (2006) Dynamic Models In Biology. Princeton: Princeton University Press. PMID 13-978-0-691-12589-3
• Schneider ED, Sagan D. (2005) Into the Cool: Energy Flow, Thermodynamics, and Life. Chicago: The University of Chicago Press ISBN 0-226-73937-6
• Klipp E, Herwig R, Kowald A, Wierling C, Lehrach H. (2005) Systems Biology in Practice. Wiley-VCH: ISBN 3-527-31078-9
• Bock G and Goode JA (eds). (2002) In Silico" Simulation of Biological Processes, Novartis Foundation Symposium 247. John Wiley & Sons ISBN 0-470-84480-9
• Kitano H (editor). (2001) Foundations of Systems Biology. MIT Press ISBN 0-262-11266-3

Articles

• Tyson JJ. 2007 Bringing cartoons to life. Nature 445:823

• Essay: Gives several examples illustrating goal stated in preface: “To understand cells as dynamic systems, mathematical tools are needed to fill the gap between molecular interactions and physiological consequences.”

• Pettinen A, Aho T, Smolander OP, Manninen T, Saarinen A, Taattola KL, Yli-Harja O, Linne ML. (2005) Simulation tools for biochemical networks: evaluation of performance and usability. Bioinformatics 21:357-363

• For examples of computational tools systems biologists use for simulation of living systems: "Simulation of dynamic biochemical systems is receiving considerable attention due to increasing availability of experimental data of complex cellular functions."

Selected external links

• Institute for Systems Biology

• Contains and introduction to, and in-depth discussion of systems biology.

Appendix A

Titles of articles reporting studies on homeostatic mechanisms by physiologists published in 2005 and 2006 in the American Journal of Physiology suite of journals, excluding cellular and molecular physiology:

• Spontaneous, homeostatic, and inflammation-induced sleep in NF-{kappa}B p50 knockout mice
• Attenuation of homeostatic responses to hypotension and glucoprivation after destruction of catecholaminergic rostral ventrolateral medulla neurons
• The Interplay Between Homeostatic Synaptic Plasticity and Functional Dendritic Compartments
• Pituitary adenylyate cyclase activating peptide (PACAP) affects homeostatic sleep regulation in healthy young men
• Temporal Regulation of the Expression Locus of Homeostatic Plasticity
• Gastrointestinal processing of Na+, Cl-, and K+ during digestion: implications for homeostatic balance in freshwater rainbow trout
• Homeostatic functions of vascular endothelial growth factor in adult microvasculature
• Homeostatic responses to caloric restriction: influence of background metabolic rate
• Cardiac endocrine function is an essential component of the homeostatic regulation network: physiological and clinical implications
• Role for the Subthreshold Currents ILeak and IH in the Homeostatic Control of Excitability in Neocortical Somatostatin-Positive Inhibitory Neurons
• Impaired glucose homeostasis and mitochondrial abnormalities in offspring of rats fed a fat-rich diet in pregnancy
• MECHANOTRANSDUCTION AND ENDOTHELIAL CELL HOMEOSTASIS: THE WISDOM OF THE CELL
• Estrogen modulates the mechanical homeostasis of mouse arterial vessels through nitric oxide
• Age-dependent alterations in Ca2+ homeostasis: role of TRPV5 and TRPV6
• Altered contractility and [Ca2+]i homeostasis in phospholemman-deficient murine myocytes: role of Na+/Ca2+ exchange
• Voltage-Gated Channels and Calcium Homeostasis in Mammalian Rod Photoreceptors
• Insulin resistance and whole body energy homeostasis in obese adolescents with fatty liver disease
• "Phosphatonins" and the regulation of phosphorus homeostasis
• Obstructive sleep apnea: wreaking havoc with homeostasis
• Impact of glutamine supplementation on glucose homeostasis during and after exercise
• Role of angiotensin in body fluid homeostasis of mice: effect of losartan on water and NaCl intakes
• Role of glucose in modulating Mg2+ homeostasis in liver cells from starved rats
• Caveolin-1 and regulation of cellular cholesterol homeostasis
• Kidney plays a major role in ammonia homeostasis after portasystemic shunting in patients with cirrhosis
• The kidney in vitamin B12 and folate homeostasis: characterization of receptors for tubular uptake of vitamins and carrier proteins
• Effects of sirolimus on mesangial cell cholesterol homeostasis: a novel mechanism for its action against lipid-mediated injury in renal allografts
• Role of Sgk1 in salt and potassium homeostasis
• Low-carbohydrate diets affect energy balance and fuel homeostasis differentially in lean and obese rats
• Changes in guinea pig gallbladder smooth muscle Ca2+ homeostasis by acute acalculous cholecystitis
• Metabolomic profiling of heat stress: hardening and recovery of homeostasis in Drosophila
• Protective effect of prenatal water restriction on offspring cardiovascular homeostasis in response to hemorrhage
• The vitamin D receptor is not required for fetal mineral homeostasis or for the regulation of placental calcium transfer in mice
• Renal oxidative vulnerability due to changes in mitochondrial-glutathione and energy homeostasis in a rat model of calcium oxalate urolithiasis
• Caffeine-induced arrhythmias in murine hearts parallel changes in cellular Ca2+ homeostasis
• Role of adenosine A1 and A3 receptors in regulation of cardiomyocyte homeostasis after mitochondrial respiratory chain injury
• Targeted inhibition of sarcoplasmic reticulum CaMKII activity results in alterations of Ca2+ homeostasis and cardiac contractility
• Fetal and neonatal exposure to AZT and low-protein diet affects glucose homeostasis: a model with implications for AIDS prevention
• Roles of Slc13a1 and Slc26a1 sulfate transporters of eel kidney in sulfate homeostasis and osmoregulation in freshwater
• Role of high-voltage-activated calcium channels in glucose-regulated {beta}-cell calcium homeostasis and insulin release
• Effects of high-fat diets with different carbohydrate-to-protein ratios on energy homeostasis in rats with impaired brain melanocortin receptor activity
• Reduced PDX-1 expression impairs islet response to insulin resistance and worsens glucose homeostasis
• Hepatic cytochrome P-450 reductase-null mice show reduced transcriptional response to quercetin and reveal physiological homeostasis between jejunum and liver
• Opposing Modifications in Intrinsic Currents and Synaptic Inputs in Post-Traumatic Mossy Cells: Evidence for Single-Cell Homeostasis in a Hyperexcitable Network
  

Template:Biology-footer