Archive:New Draft of the Week
The New Draft of the Week is a chance to highlight a recently created Citizendium article that has just started down the road of becoming a Citizendium masterpiece.
It is chosen each week by vote in a manner similar to that of its sister project, the Article of the Week.
Add New Nominees Here
To add a new nominee or vote for an existing nominee, click edit for this section and follow the instructions
| Nominated article | Vote Score |
Supporters | Specialist supporters | Date created |
|---|---|---|---|---|
| Tall tale | 3 | Daniel Mietchen; Howard C. Berkowitz; Paul Wormer; |
9 March 2010 | |
| Aeneid | 1 | Daniel Mietchen 23:38, 10 April 2010 (UTC) | 28 March 2010 | |
If you want to see how these nominees will look on the CZ home page (if selected as a winner), scroll down a little bit.
Transclusion of the above nominees (to be done by an Administrator)
- Transclude each of the nominees in the above "Table of Nominee" as per the instructions at Template:Featured Article Candidate.
- Then add the transcluded article to the list in the next section below, using the {{Featured Article Candidate}} template.
View Current Transcluded Nominees (after they have been transcluded by an Administrator)
The next New Draft of the Week will be the article with the most votes at 1 AM UTC on Thursday, 29 April, 2010.
| Nominated article | Supporters | Specialist supporters | Dates | Score | ||||
|---|---|---|---|---|---|---|---|---|
This article is about the geometrical concept. For other uses of the term Plane, please see Plane (disambiguation).
In Euclidean geometry, a plane is an abstract concept that models the common notion of a flat surface — without depressions, protrusions, holes and a boundary — that for any two of its points entirely contains the straight line joining them. Assuming a common (intuitive, physical) idea of the geometry of space, "plane" can be defined in terms of distances, orthogonality, lines, coordinates etc. In a more abstract approach (vector spaces) planes are defined as two-dimensional affine subspaces. In an axiomatic approach, basic concepts of elementary geometry, such as "point", "line" and "plane", are undefined primitives.  (CC) Image: Dina Tsirelson The surface of this metallic body consists of rectangles situated in various planes. Non-axiomatic approachDefinitionsA remarkTo define a plane is more complicated than it may seem. It is tempting to define a plane as a surface with zero curvature, where a surface is defined as a geometric object having length and breadth but no depth. However, this is not a good idea; such definitions are useless in mathematics, since they cannot be used when proving theorems. Planes are treated by elementary geometry, but the notions of surface and curvature are not elementary, they need more advanced mathematics and more sophisticated definitions. Fortunately, it is possible to define a line via more elementary notions, and this way is preferred in mathematics. Still, the definitions given below are tentative. They are criticized afterwards, see axiomatic approach. The definitions of "plane" given below may be compared with the definition of a circle as consisting of those points in a plane that are a given distance (the radius) away from a given point (the center). A circle is a set of points chosen according to their relation to some given parameters (center and radius). Similarly, a plane is a set of points chosen according to their relation to some given objects (points, lines etc). However, a circle determines its center and radius uniquely; for a plane, the situation is different. Four equivalent definitions of "plane" are given below. Any other definition is equally acceptable provided that it is equivalent to these. Note that a part of a plane is not a plane. Likewise, a line segment is not a line. Below, all points, lines and planes are situated in the space (assumed to be a three-dimensional Euclidean space), and by lines we mean straight lines. Definition via distancesLet two different points A and B be given. The set of all points C that are equally far from A and B — that is, — is a plane. This is the plane orthogonal to the line AB through the middle point of the line segment AB. Definition via right angles (orthogonality)Let two different points A and B be given. The set of all points C such that the lines AB and AC are orthogonal (that is, the angle BAC is right) is a plane. This is the plane orthogonal to the line AB through the point A. Definition via linesLet three points A, B and C be given, not lying on a line. Consider the lines DE for all points D (different from B) on the line AB and all points E (also different from B) on the line BC. The union of all these lines, together with the point B, is a plane. This is the plane through A, B and C. In other words, this plane is the set of all points F such that either F coincides with B or there exists a line through F that intersects the lines AB and BC (in distinct points). Definition via Cartesian coordinatesIn terms of Cartesian coordinates x, y, z ascribed to every point of the space, a plane is the set of points whose coordinates satisfy the linear equation
Here real numbers a, b, c and d are parameters such that at least one of a, b, c does not vanish. Some properties of planesMost basic propertiesFor any three points not situated in the same straight line there exists one and only one plane that contains these three points. If two points of a straight line lie in a plane, then every point of the line lies in that plane. If two planes have a common point then they have at least a second point in common. Every plane contains at least three points not lying in the same straight line, and the space contains at least four points not lying in a plane. Further propertiesTwo planes either do not intersect (are parallel), or intersect in a line, or coincide. A line either does not intersect a plane (is parallel to it), or intersects it in a single point, or is contained in the plane. Two lines perpendicular to the same plane are parallel to each other (or coincide). Two planes perpendicular to the same line are parallel to each other (or coincide). Axiomatic approachWhat is wrong with the definitions given above?The definitions given above assume implicitly that the 3-dimensional Euclidean space is already defined, together with (at least one of) such notions as distances, angles, straight lines, Cartesian coordinates, while planes are not defined yet. However, this situation never appears in mathematical theory. In the axiomatic approach points, lines and planes are undefined primitives. The modern approach (below) defines planes in a completely different way. How does it workAxiomatic approach is similar to chess in the following aspect. A chess piece, say a rook, cannot be defined before the whole chess game is defined, since such a phrase as "the rook moves horizontally or vertically, forward or back, through any number of unoccupied squares" makes no sense unless it is already known that "chess is played on a square board of eight rows and eight columns" etc. And conversely, the whole chess game cannot be defined before each piece is defined; the properties of the rook are an indispensable part of the rules of the game. No chess without rooks, no rooks outside chess! One must introduce the game, its pieces and their properties in a single combined definition. Likewise, Euclidean space, its points, lines, planes and their properties are introduced simultaneously in a set of 20 assumptions known as Hilbert's axioms of Euclidean geometry.[1] The "most basic properties of planes" listed above are roughly the plane-related assumptions (Hilbert's axioms), while "further properties" are the first plane-related consequences (theorems). Modern approachThe modern approach defines the three-dimensional Euclidean space more algebraically, via linear spaces and quadratic forms, namely, as a real affine space whose difference space is a three-dimensional inner product space. For further details see Affine space#Euclidean space and space (mathematics). In this approach a plane in an n-dimensional affine space (n ≥ 2) is defined as a (proper or improper) two-dimensional affine subspace. A less formal version of this approach uses points, vectors and scalar product (called also dot product or inner product) of vectors without mentioning linear and affine spaces. Optionally, Cartesian coordinates of points and vectors are used. See algebraic equations below. There, in particular, equivalence between the definition via right angles (orthogonality) and the definition via Cartesian coordinates is explained. Plane geometryPlane geometry (also called "planar geometry") is a part of solid geometry that restricts itself to a single plane ("the plane") treated as a geometric universe. In other words, plane geometry is the theory of the two-dimensional Euclidean space, while solid geometry is the theory of the three-dimensional Euclidean space. Plane geometry studies the properties of plane figures (and configurations). Plane figures in elementary geometry are sets of points, lines, line segments and sometimes curves that fall on the same plane. For example, triangles, polygons and circles. In plane geometry every figure is plane, in contrast to solid geometry. Algebraic equationsIn analytic geometry several closely related algebraic equations are known for a plane in three-dimensional Euclidean space. A few algebraic representations will be discussed. Point-normal representationOne such equation is illustrated in the figure. Point P is an arbitrary point in the plane and O (the origin) is drawn outside the plane. The point A in the plane is chosen such that vector is orthogonal to the plane. The collinear vector is a unit (length 1) vector normal (perpendicular) to the plane which is known as the normal of the plane in point A. Note that d is the distance of O to the plane. The following relation holds for an arbitrary point P in the plane (according to the definition via right angles): This equation for the plane can be rewritten in terms of coordinates with respect to a Cartesian frame with origin in O. Dropping arrows for component vectors (real triplets) that are written bold, we find with and The definition via Cartesian coordinates is thus derived from the definition via right angles. Moreover, the Hesse normal form for the plane (called after the 19th century mathematician Ludwig Otto Hesse) is obtained, it is characterized by the use of a unit-length vector rather than an arbitrary vector orthogonal to the plane. Conversely, the definition via right angles can be derived from the definition via Cartesian coordinates as follows. Given a linear equation for a plane we write It follows that Hence we find the same orthogonality relation, where f , d, and n0 are collinear. The equation may also be written in the following mnemonically convenient form which is the equation for a plane through a point A perpendicular to . Three-point representationThe figure shows a plane that by definition passes through three different points A, B, and C that are not on one line. The point P is an arbitrary point in the plane and the reference point O is again drawn outside the plane, but the case that the plane passes through O is not excluded. Referring to figure 2 we introduce the following definitions Clearly the following two non-collinear vectors belong to the plane Because a plane (an affine space), with a given fixed point as origin is a 2-dimensional linear space and two non-collinear vectors with "tails" in the origin are linearly independent, it follows that any vector in the plane can be written as a linear combination of these two non-collinear vectors. (This is also expressed as: Any vector in the plane can be decomposed into components along the two non-collinear vectors.) In particular, taking A as origin in the plane, The real numbers λ and μ specify the direction of . Hence the following equation for the position vector of the arbitrary point P in the plane: is known as the point-direction representation of the plane. This representation is equal to the three-point representation where , , and are the position vectors of the three points that define the plane. Writing for the position vector of the arbitrary point P in the plane we find that the real triplet (ξ1, ξ2, ξ3) with ξ1 + ξ1 + ξ1 = 1 forms a set of coordinates for P. The numbers {ξ1, ξ2, ξ3 | ξ1+ ξ2+ ξ3 = 1 } are known as the barycentric coordinates of P. It is trivial to go from barycentric coordinates to the "three-point representation", Beyond mathematicsIn industry, a surface plate[2] is a piece of cast iron or other appropriate material whose surface (or rather a part of it) is made as close as possible to a geometric plane (or rather a part of it, usually a square). An old method of their manufacturing is the three-plate method: three roughly flat surfaces become more and more flat when rubbing against each other: first and second; second and third; third and first; first and second again, and so on. It is possible to achieve a surface close to a plane up to 10–5 of its size. Reference
|
Daniel Mietchen ; Meg Ireland; Chunbum Park |
Peter Schmitt | 5
|
Current Winner (to be selected and implemented by an Administrator)
To change, click edit and follow the instructions, or see documentation at {{Featured Article}}.
| The metadata subpage is missing. You can start it via filling in this form or by following the instructions that come up after clicking on the [show] link to the right. | |||
|---|---|---|---|
|
In Euclidean geometry, a plane is an abstract concept that models the common notion of a flat surface — without depressions, protrusions, holes and a boundary — that for any two of its points entirely contains the straight line joining them.
Assuming a common (intuitive, physical) idea of the geometry of space, "plane" can be defined in terms of distances, orthogonality, lines, coordinates etc. In a more abstract approach (vector spaces) planes are defined as two-dimensional affine subspaces. In an axiomatic approach, basic concepts of elementary geometry, such as "point", "line" and "plane", are undefined primitives.

The surface of this metallic body consists of rectangles situated in various planes.
Non-axiomatic approach
Definitions
A remark
To define a plane is more complicated than it may seem.
It is tempting to define a plane as a surface with zero curvature, where a surface is defined as a geometric object having length and breadth but no depth. However, this is not a good idea; such definitions are useless in mathematics, since they cannot be used when proving theorems. Planes are treated by elementary geometry, but the notions of surface and curvature are not elementary, they need more advanced mathematics and more sophisticated definitions. Fortunately, it is possible to define a line via more elementary notions, and this way is preferred in mathematics. Still, the definitions given below are tentative. They are criticized afterwards, see axiomatic approach.
The definitions of "plane" given below may be compared with the definition of a circle as consisting of those points in a plane that are a given distance (the radius) away from a given point (the center). A circle is a set of points chosen according to their relation to some given parameters (center and radius). Similarly, a plane is a set of points chosen according to their relation to some given objects (points, lines etc). However, a circle determines its center and radius uniquely; for a plane, the situation is different.
Four equivalent definitions of "plane" are given below. Any other definition is equally acceptable provided that it is equivalent to these. Note that a part of a plane is not a plane. Likewise, a line segment is not a line.
Below, all points, lines and planes are situated in the space (assumed to be a three-dimensional Euclidean space), and by lines we mean straight lines.
Definition via distances
Let two different points A and B be given. The set of all points C that are equally far from A and B — that is,
— is a plane.
This is the plane orthogonal to the line AB through the middle point of the line segment AB.
Definition via right angles (orthogonality)
Let two different points A and B be given. The set of all points C such that the lines AB and AC are orthogonal (that is, the angle BAC is right) is a plane.
This is the plane orthogonal to the line AB through the point A.
Definition via lines
Let three points A, B and C be given, not lying on a line. Consider the lines DE for all points D (different from B) on the line AB and all points E (also different from B) on the line BC. The union of all these lines, together with the point B, is a plane.
This is the plane through A, B and C.
In other words, this plane is the set of all points F such that either F coincides with B or there exists a line through F that intersects the lines AB and BC (in distinct points).
Definition via Cartesian coordinates
In terms of Cartesian coordinates x, y, z ascribed to every point of the space, a plane is the set of points whose coordinates satisfy the linear equation
- .
Here real numbers a, b, c and d are parameters such that at least one of a, b, c does not vanish.
Some properties of planes
Most basic properties
For any three points not situated in the same straight line there exists one and only one plane that contains these three points.
If two points of a straight line lie in a plane, then every point of the line lies in that plane.
If two planes have a common point then they have at least a second point in common.
Every plane contains at least three points not lying in the same straight line, and the space contains at least four points not lying in a plane.
Further properties
Two planes either do not intersect (are parallel), or intersect in a line, or coincide.
A line either does not intersect a plane (is parallel to it), or intersects it in a single point, or is contained in the plane.
Two lines perpendicular to the same plane are parallel to each other (or coincide).
Two planes perpendicular to the same line are parallel to each other (or coincide).
Axiomatic approach
What is wrong with the definitions given above?
The definitions given above assume implicitly that the 3-dimensional Euclidean space is already defined, together with (at least one of) such notions as distances, angles, straight lines, Cartesian coordinates, while planes are not defined yet. However, this situation never appears in mathematical theory.
In the axiomatic approach points, lines and planes are undefined primitives.
The modern approach (below) defines planes in a completely different way.
How does it work
Axiomatic approach is similar to chess in the following aspect.
A chess piece, say a rook, cannot be defined before the whole chess game is defined, since such a phrase as "the rook moves horizontally or vertically, forward or back, through any number of unoccupied squares" makes no sense unless it is already known that "chess is played on a square board of eight rows and eight columns" etc. And conversely, the whole chess game cannot be defined before each piece is defined; the properties of the rook are an indispensable part of the rules of the game. No chess without rooks, no rooks outside chess! One must introduce the game, its pieces and their properties in a single combined definition.
Likewise, Euclidean space, its points, lines, planes and their properties are introduced simultaneously in a set of 20 assumptions known as Hilbert's axioms of Euclidean geometry.[1] The "most basic properties of planes" listed above are roughly the plane-related assumptions (Hilbert's axioms), while "further properties" are the first plane-related consequences (theorems).
Modern approach
The modern approach defines the three-dimensional Euclidean space more algebraically, via linear spaces and quadratic forms, namely, as a real affine space whose difference space is a three-dimensional inner product space. For further details see Affine space#Euclidean space and space (mathematics).
In this approach a plane in an n-dimensional affine space (n ≥ 2) is defined as a (proper or improper) two-dimensional affine subspace.
A less formal version of this approach uses points, vectors and scalar product (called also dot product or inner product) of vectors without mentioning linear and affine spaces. Optionally, Cartesian coordinates of points and vectors are used. See algebraic equations below. There, in particular, equivalence between the definition via right angles (orthogonality) and the definition via Cartesian coordinates is explained.
Plane geometry
Plane geometry (also called "planar geometry") is a part of solid geometry that restricts itself to a single plane ("the plane") treated as a geometric universe. In other words, plane geometry is the theory of the two-dimensional Euclidean space, while solid geometry is the theory of the three-dimensional Euclidean space.
Plane geometry studies the properties of plane figures (and configurations). Plane figures in elementary geometry are sets of points, lines, line segments and sometimes curves that fall on the same plane. For example, triangles, polygons and circles. In plane geometry every figure is plane, in contrast to solid geometry.
Algebraic equations
In analytic geometry several closely related algebraic equations are known for a plane in three-dimensional Euclidean space. A few algebraic representations will be discussed.
Point-normal representation
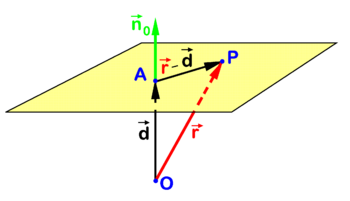
One such equation is illustrated in the figure. Point P is an arbitrary point in the plane and O (the origin) is drawn outside the plane. The point A in the plane is chosen such that vector
is orthogonal to the plane. The collinear vector
is a unit (length 1) vector normal (perpendicular) to the plane which is known as the normal of the plane in point A. Note that d is the distance of O to the plane. The following relation holds for an arbitrary point P in the plane (according to the definition via right angles):
This equation for the plane can be rewritten in terms of coordinates with respect to a Cartesian frame with origin in O. Dropping arrows for component vectors (real triplets) that are written bold, we find
with
and
The definition via Cartesian coordinates is thus derived from the definition via right angles.
Moreover, the Hesse normal form for the plane (called after the 19th century mathematician Ludwig Otto Hesse) is obtained,
it is characterized by the use of a unit-length vector rather than an arbitrary vector orthogonal to the plane.
Conversely, the definition via right angles can be derived from the definition via Cartesian coordinates as follows. Given a linear equation for a plane
we write
It follows that
Hence we find the same orthogonality relation,
where f , d, and n0 are collinear. The equation may also be written in the following mnemonically convenient form
which is the equation for a plane through a point A perpendicular to .
Three-point representation
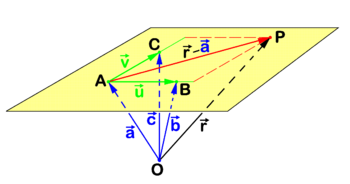
The figure shows a plane that by definition passes through three different points A, B, and C that are not on one line. The point P is an arbitrary point in the plane and the reference point O is again drawn outside the plane, but the case that the plane passes through O is not excluded. Referring to figure 2 we introduce the following definitions
Clearly the following two non-collinear vectors belong to the plane
Because a plane (an affine space), with a given fixed point as origin is a 2-dimensional linear space and two non-collinear vectors with "tails" in the origin are linearly independent, it follows that any vector in the plane can be written as a linear combination of these two non-collinear vectors. (This is also expressed as: Any vector in the plane can be decomposed into components along the two non-collinear vectors.) In particular, taking A as origin in the plane,
The real numbers λ and μ specify the direction of . Hence the following equation for the position vector of the arbitrary point P in the plane:
is known as the point-direction representation of the plane. This representation is equal to the three-point representation
where , , and are the position vectors of the three points that define the plane.
Writing for the position vector of the arbitrary point P in the plane
we find that the real triplet (ξ1, ξ2, ξ3) with ξ1 + ξ1 + ξ1 = 1 forms a set of coordinates for P. The numbers {ξ1, ξ2, ξ3 | ξ1+ ξ2+ ξ3 = 1 } are known as the barycentric coordinates of P. It is trivial to go from barycentric coordinates to the "three-point representation",
Beyond mathematics
In industry, a surface plate[2] is a piece of cast iron or other appropriate material whose surface (or rather a part of it) is made as close as possible to a geometric plane (or rather a part of it, usually a square). An old method of their manufacturing is the three-plate method: three roughly flat surfaces become more and more flat when rubbing against each other: first and second; second and third; third and first; first and second again, and so on. It is possible to achieve a surface close to a plane up to 10–5 of its size.
Reference
- ↑ D. Hilbert, Grundlagen der Geometrie, B. G. Teubner, Leipzig (1899) 2nd German edition
- ↑ Miller, Jimmie A. (5 October 2004). Surface Plate. University of North Carolina. Retrieved on 29 October 2013.
Previous Winners
 Steam [r]: The vapor (or gaseous) phase of water (H2O). [e]
Steam [r]: The vapor (or gaseous) phase of water (H2O). [e] Wasan [r]: Classical Japanese mathematics that flourished during the Edo Period from the 17th to mid-19th centuries. [e]
Wasan [r]: Classical Japanese mathematics that flourished during the Edo Period from the 17th to mid-19th centuries. [e] Racism in Australia [r]: The history of racism and restrictive immigration policies in the Commonwealth of Australia. [e]
Racism in Australia [r]: The history of racism and restrictive immigration policies in the Commonwealth of Australia. [e]- Think tank [r]: Add brief definition or description
 Les Paul [r]: (9 June 1915 – 13 August 2009) American innovator, inventor, musician and songwriter, who was notably a pioneer in the development of the solid-body electric guitar. [e]
Les Paul [r]: (9 June 1915 – 13 August 2009) American innovator, inventor, musician and songwriter, who was notably a pioneer in the development of the solid-body electric guitar. [e] Zionism [r]: The ideology that Jews should form a Jewish state in what is traced as the Biblical area of Palestine; there are many interpretations, including the boundaries of such a state and its criteria for citizenship [e] (September 3)
Zionism [r]: The ideology that Jews should form a Jewish state in what is traced as the Biblical area of Palestine; there are many interpretations, including the boundaries of such a state and its criteria for citizenship [e] (September 3) Earth's atmosphere [r]: An envelope of gas that surrounds the Earth and extends from the Earth's surface out thousands of kilometres, becoming increasingly thinner (less dense) with distance but always held in place by Earth's gravitational pull. [e] (August 27)
Earth's atmosphere [r]: An envelope of gas that surrounds the Earth and extends from the Earth's surface out thousands of kilometres, becoming increasingly thinner (less dense) with distance but always held in place by Earth's gravitational pull. [e] (August 27) Joshua Lawrence Chamberlain [r]: U.S. educator deeply bonded to Bowdoin College, from undergraduate to President; American Civil War general and recipient of the Medal of Honor; Governor of Maine [e] (August 20)
Joshua Lawrence Chamberlain [r]: U.S. educator deeply bonded to Bowdoin College, from undergraduate to President; American Civil War general and recipient of the Medal of Honor; Governor of Maine [e] (August 20) The Sporting Life (album) [r]: A 1994 studio album recorded by Diamanda Galás and John Paul Jones. [e] (August 13}
The Sporting Life (album) [r]: A 1994 studio album recorded by Diamanda Galás and John Paul Jones. [e] (August 13} The Rolling Stones [r]: Famous and influential English blues rock group formed in 1962, known for their albums Let It Bleed and Sticky Fingers, and songs '(I Can't Get No) Satisfaction' and 'Start Me Up'. [e] (August 5)
The Rolling Stones [r]: Famous and influential English blues rock group formed in 1962, known for their albums Let It Bleed and Sticky Fingers, and songs '(I Can't Get No) Satisfaction' and 'Start Me Up'. [e] (August 5) Euler angles [r]: three rotation angles that describe any rotation of a 3-dimensional object. [e] (July 30)
Euler angles [r]: three rotation angles that describe any rotation of a 3-dimensional object. [e] (July 30) Chester Nimitz [r]: United States Navy admiral (1885-1966) who was Commander in Chief, Pacific and Pacific Ocean Areas in World War II [e] (July 23)
Chester Nimitz [r]: United States Navy admiral (1885-1966) who was Commander in Chief, Pacific and Pacific Ocean Areas in World War II [e] (July 23) Heat [r]: A form of energy that flows spontaneously from hotter to colder bodies that are in thermal contact. [e] (July 16)
Heat [r]: A form of energy that flows spontaneously from hotter to colder bodies that are in thermal contact. [e] (July 16) Continuum hypothesis [r]: A statement about the size of the continuum, i.e., the number of elements in the set of real numbers. [e] (July 9)
Continuum hypothesis [r]: A statement about the size of the continuum, i.e., the number of elements in the set of real numbers. [e] (July 9) Hawaiian alphabet [r]: The form of writing used in the Hawaiian Language [e] (July 2)
Hawaiian alphabet [r]: The form of writing used in the Hawaiian Language [e] (July 2) Now and Zen [r]: A 1988 studio album recorded by Robert Plant, with guest contributions from Jimmy Page. [e] (June 25)
Now and Zen [r]: A 1988 studio album recorded by Robert Plant, with guest contributions from Jimmy Page. [e] (June 25) Wrench (tool) [r]: A fastening tool used to tighten or loosen threaded fasteners, with one end that makes firm contact with flat surfaces of the fastener, and the other end providing a means of applying force [e] (June 18)
Wrench (tool) [r]: A fastening tool used to tighten or loosen threaded fasteners, with one end that makes firm contact with flat surfaces of the fastener, and the other end providing a means of applying force [e] (June 18) Air preheater [r]: A general term to describe any device designed to preheat the combustion air used in a fuel-burning furnace for the purpose of increasing the thermal efficiency of the furnace. [e] (June 11)
Air preheater [r]: A general term to describe any device designed to preheat the combustion air used in a fuel-burning furnace for the purpose of increasing the thermal efficiency of the furnace. [e] (June 11) 2009 H1N1 influenza virus [r]: A contagious influenza A virus discovered in April 2009, commonly known as swine flu. [e] (June 4)
2009 H1N1 influenza virus [r]: A contagious influenza A virus discovered in April 2009, commonly known as swine flu. [e] (June 4) Gasoline [r]: A fuel for spark-ignited internal combustion engines derived from petroleum crude oil. [e] (21 May)
Gasoline [r]: A fuel for spark-ignited internal combustion engines derived from petroleum crude oil. [e] (21 May) John Brock [r]: Fictional British secret agent who starred in three 1960s thrillers by Desmond Skirrow. [e] (8 May)
John Brock [r]: Fictional British secret agent who starred in three 1960s thrillers by Desmond Skirrow. [e] (8 May) McGuffey Readers [r]: A set of highly influential school textbooks used in the 19th and early 20th centuries in the elementary grades in the United States. [e] (14 Apr)
McGuffey Readers [r]: A set of highly influential school textbooks used in the 19th and early 20th centuries in the elementary grades in the United States. [e] (14 Apr) Vector rotation [r]: Process of rotating one unit vector into a second unit vector. [e] (7 Apr)
Vector rotation [r]: Process of rotating one unit vector into a second unit vector. [e] (7 Apr) Leptin [r]: Hormone secreted by adipocytes that regulates appetite. [e] (31 Mar)
Leptin [r]: Hormone secreted by adipocytes that regulates appetite. [e] (31 Mar) Kansas v. Crane [r]: A 2002 decision of the Supreme Court of the United States, ruling that a person could not be adjudicated a sexual predator and put in indefinite medical confinement, purely on assessment of an emotional disorder, but such action required proof of a likelihood of uncontrollable impulse presenting a clear and present danger. [e] (24 Mar)
Kansas v. Crane [r]: A 2002 decision of the Supreme Court of the United States, ruling that a person could not be adjudicated a sexual predator and put in indefinite medical confinement, purely on assessment of an emotional disorder, but such action required proof of a likelihood of uncontrollable impulse presenting a clear and present danger. [e] (24 Mar) Punch card [r]: A term for cards used for storing information. Herman Hollerith is credited with the invention of the media for storing information from the United States Census of 1890. [e] (17 Mar)
Punch card [r]: A term for cards used for storing information. Herman Hollerith is credited with the invention of the media for storing information from the United States Census of 1890. [e] (17 Mar) Jass–Belote card games [r]: A group of trick-taking card games in which the Jack and Nine of trumps are the highest trumps. [e] (10 Mar)
Jass–Belote card games [r]: A group of trick-taking card games in which the Jack and Nine of trumps are the highest trumps. [e] (10 Mar) Leptotes (orchid) [r]: A genus of orchids formed by nine small species that exist primarily in the dry jungles of South and Southeast Brazil. [e] (3 Mar)
Leptotes (orchid) [r]: A genus of orchids formed by nine small species that exist primarily in the dry jungles of South and Southeast Brazil. [e] (3 Mar) Worm (computers) [r]: A form of malware that can spread, among networked computers, without human interaction. [e] (24 Feb)
Worm (computers) [r]: A form of malware that can spread, among networked computers, without human interaction. [e] (24 Feb) Joseph Black [r]: Add brief definition or description (11 Feb 2009)
Joseph Black [r]: Add brief definition or description (11 Feb 2009) Sympathetic magic [r]: Add brief definition or description (17 Jan 2009)
Sympathetic magic [r]: Add brief definition or description (17 Jan 2009) Dien Bien Phu [r]: Add brief definition or description (25 Dec)
Dien Bien Phu [r]: Add brief definition or description (25 Dec)- Blade Runner [r]: Add brief definition or description (25 Nov)
 Piquet [r]: Add brief definition or description (18 Nov)
Piquet [r]: Add brief definition or description (18 Nov) Crash of 2008 [r]: Add brief definition or description (23 Oct)
Crash of 2008 [r]: Add brief definition or description (23 Oct)- Information Management [r]: Add brief definition or description (31 Aug)
 Battle of Gettysburg [r]: Add brief definition or description (8 July)
Battle of Gettysburg [r]: Add brief definition or description (8 July) Drugs banned from the Olympics [r]: Add brief definition or description (1 July)
Drugs banned from the Olympics [r]: Add brief definition or description (1 July) Sea glass [r]: Add brief definition or description (24 June)
Sea glass [r]: Add brief definition or description (24 June) Dazed and Confused (Led Zeppelin song) [r]: Add brief definition or description (17 June)
Dazed and Confused (Led Zeppelin song) [r]: Add brief definition or description (17 June) Hirohito [r]: Add brief definition or description (10 June)
Hirohito [r]: Add brief definition or description (10 June) Henry Kissinger [r]: Add brief definition or description (3 June)
Henry Kissinger [r]: Add brief definition or description (3 June)- Palatalization [r]: Add brief definition or description (27 May)
 Intelligence on the Korean War [r]: Add brief definition or description (20 May)
Intelligence on the Korean War [r]: Add brief definition or description (20 May) Trinity United Church of Christ, Chicago [r]: Add brief definition or description (13 May)
Trinity United Church of Christ, Chicago [r]: Add brief definition or description (13 May) BIOS [r]: Add brief definition or description (6 May)
BIOS [r]: Add brief definition or description (6 May) Miniature Fox Terrier [r]: Add brief definition or description (23 April)
Miniature Fox Terrier [r]: Add brief definition or description (23 April) Joseph II [r]: Add brief definition or description (15 Apr)
Joseph II [r]: Add brief definition or description (15 Apr) British and American English [r]: Add brief definition or description (7 Apr)
British and American English [r]: Add brief definition or description (7 Apr) Count Rumford [r]: Add brief definition or description (1 April)
Count Rumford [r]: Add brief definition or description (1 April) Whale meat [r]: Add brief definition or description (25 March)
Whale meat [r]: Add brief definition or description (25 March) Naval guns [r]: Add brief definition or description (18 March)
Naval guns [r]: Add brief definition or description (18 March) Sri Lanka [r]: Add brief definition or description (11 March)
Sri Lanka [r]: Add brief definition or description (11 March) Led Zeppelin [r]: Add brief definition or description (4 March)
Led Zeppelin [r]: Add brief definition or description (4 March) Martin Luther [r]: Add brief definition or description (20 February)
Martin Luther [r]: Add brief definition or description (20 February) Cosmology [r]: Add brief definition or description (4 February)
Cosmology [r]: Add brief definition or description (4 February) Ernest Rutherford [r]: Add brief definition or description(28 January)
Ernest Rutherford [r]: Add brief definition or description(28 January) Edinburgh [r]: Add brief definition or description (21 January)
Edinburgh [r]: Add brief definition or description (21 January) Russian Revolution of 1905 [r]: Add brief definition or description (8 January 2008)
Russian Revolution of 1905 [r]: Add brief definition or description (8 January 2008) Phosphorus [r]: Add brief definition or description (31 December)
Phosphorus [r]: Add brief definition or description (31 December) John Tyler [r]: Add brief definition or description (6 December)
John Tyler [r]: Add brief definition or description (6 December) Banana [r]: Add brief definition or description (22 November)
Banana [r]: Add brief definition or description (22 November) Augustin-Louis Cauchy [r]: Add brief definition or description (15 November)
Augustin-Louis Cauchy [r]: Add brief definition or description (15 November)- B-17 Flying Fortress (bomber) [r]: Add brief definition or description - 8 November 2007
 Red Sea Urchin [r]: Add brief definition or description - 1 November 2007
Red Sea Urchin [r]: Add brief definition or description - 1 November 2007 Symphony [r]: Add brief definition or description - 25 October 2007
Symphony [r]: Add brief definition or description - 25 October 2007 Oxygen [r]: Add brief definition or description - 18 October 2007
Oxygen [r]: Add brief definition or description - 18 October 2007 Origins and architecture of the Taj Mahal [r]: Add brief definition or description - 11 October 2007
Origins and architecture of the Taj Mahal [r]: Add brief definition or description - 11 October 2007 Fossilization (palaeontology) [r]: Add brief definition or description - 4 October 2007
Fossilization (palaeontology) [r]: Add brief definition or description - 4 October 2007 Cradle of Humankind [r]: Add brief definition or description - 27 September 2007
Cradle of Humankind [r]: Add brief definition or description - 27 September 2007 John Adams [r]: Add brief definition or description - 20 September 2007
John Adams [r]: Add brief definition or description - 20 September 2007 Quakers [r]: Add brief definition or description - 13 September 2007
Quakers [r]: Add brief definition or description - 13 September 2007 Scarborough Castle [r]: Add brief definition or description - 6 September 2007
Scarborough Castle [r]: Add brief definition or description - 6 September 2007 Jane Addams [r]: Add brief definition or description - 30 August 2007
Jane Addams [r]: Add brief definition or description - 30 August 2007 Epidemiology [r]: Add brief definition or description - 23 August 2007
Epidemiology [r]: Add brief definition or description - 23 August 2007 Gay community [r]: Add brief definition or description - 16 August 2007
Gay community [r]: Add brief definition or description - 16 August 2007 Edward I [r]: Add brief definition or description - 9 August 2007
Edward I [r]: Add brief definition or description - 9 August 2007
Rules and Procedure
Rules
- The primary criterion of eligibility for a new draft is that it must have been ranked as a status 1 or 2 (developed or developing), as documented in the History of the article's Metadate template, no more than one month before the date of the next selection (currently every Thursday).
- Any Citizen may nominate a draft.
- No Citizen may have nominated more than one article listed under "current nominees" at a time.
- The article's nominator is indicated simply by the first name in the list of votes (see below).
- At least for now--while the project is still small--you may nominate and vote for drafts of which you are a main author.
- An article can be the New Draft of the Week only once. Nominated articles that have won this honor should be removed from the list and added to the list of previous winners.
- Comments on nominations should be made on the article's talk page.
- Any draft will be deleted when it is past its "last date eligible". Don't worry if this happens to your article; consider nominating it as the Article of the Week.
- If an editor believes that a nominee in his or her area of expertise is ineligible (perhaps due to obvious and embarrassing problems) he or she may remove the draft from consideration. The editor must indicate the reasons why he has done so on the nominated article's talk page.
Nomination
See above section "Add New Nominees Here".
Voting
- To vote, add your name and date in the Supporters column next to an article title, after other supporters for that article, by signing
<br />~~~~. (The date is necessary so that we can determine when the last vote was added.) Your vote is alloted a score of 1. - Add your name in the Specialist supporters column only if you are an editor who is an expert about the topic in question. Your vote is alloted a score of 1 for articles that you created and 2 for articles that you did not create.
- You may vote for as many articles as you wish, and each vote counts separately, but you can only nominate one at a time; see above. You could, theoretically, vote for every nominated article on the page, but this would be pointless.
Ranking
- The list of articles is sorted by number of votes first, then alphabetically.
- Admins should make sure that the votes are correctly tallied, but anyone may do this. Note that "Specialist Votes" are worth 3 points.
Updating
- Each Thursday, one of the admins listed below should move the winning article to the Current Winner section of this page, announce the winner on Citizendium-L and update the "previous winning drafts" section accordingly.
- The winning article will be the article at the top of the list (ie the one with the most votes).
- In the event of two or more having the same number of votes :
- The article with the most specialist supporters is used. Should this fail to produce a winner, the article appearing first by English alphabetical order is used.
- The remaining winning articles are guaranteed this position in the following weeks, again in alphabetical order. No further voting should take place on these, which remain at the top of the table with notices to that effect. Further nominations and voting take place to determine future winning articles for the following weeks.
- Winning articles may be named New Draft of the Week beyond their last eligible date if their circumstances are so described above.
- The article with the most specialist supporters is used. Should this fail to produce a winner, the article appearing first by English alphabetical order is used.
Administrators
The Administrators of this program are the same as the admins for CZ:Article of the Week.
References
See Also
- CZ:Article of the Week
- CZ:Markup tags for partial transclusion of selected text in an article
- CZ:Monthly Write-a-Thon
| Citizendium Initiatives | ||
|---|---|---|
| Eduzendium | Featured Article | Recruitment | Subpages | Core Articles | Uncategorized pages | Requested Articles | Feedback Requests | Wanted Articles |
|width=10% align=center style="background:#F5F5F5"| |}