Harmonic oscillator (classical)

Harmonic oscillator: mass m oscillates between −x and x. Equilibrium at x = 0.

In physics, a harmonic oscillator appears frequently as a simple model for many different types of phenomena. The simplest physical realization of a harmonic oscillator consists of a mass m on which a force acts that is linear in a displacement from equilibrium. By Hooke's law a spring gives to very good approximation a force that is linear for small displacements and so figure 1 shows a simple realization of a harmonic oscillator. The uppermost mass m feels a force acting to the right equal to k x, where k is Hooke's spring constant (a positive number). The mass in the middle is in equilibrium, and the mass at the bottom feels a force to the left equal to −k x. The force executed by the springs always acts so as to restore the mass back toward its equilibrium position. If the mass is pulled out of equilibrium to x = A and then let go, the mass will (in an ideal setup) oscillate forever between ±A. In practice, energy will be lost due to friction of the atoms in the spring, so that the oscillation will die out after some time.

Mathematical description

The motion of the mass as a function of time t may be obtained from Newton's second law (F = ma). Bringing the force F and the acceleration a (times mass m) to the same side of Newton's equation, the harmonic oscillator equation becomes the equation on the left,

$m{\ddot {x}}+kx=0\;\Longrightarrow \;{\ddot {x}}=-{\frac {k}{m}}x\quad {\hbox{with}}\quad {\ddot {x}}\equiv {\frac {d^{2}x}{dt^{2}}}.$

We see that the second derivative of x is proportional to −x. There are several functions known to have this property (sine, cosine, exponent with imaginary argument), we choose fairly arbitrarily the cosine as a trial function. The oscillator equation is a second order ordinary differential equation and its general solution contains two integration constants. Further the unit of time is undetermined and hence we scale time by a real number ω. In total the trial function is

$x(t)=A\cos(\omega t+\phi )\;,$

where the integration constants A and φ are to be determined from the initial conditions. Substitution into the Newton equation gives

$-Am\omega ^{2}\cos(\omega t+\phi )+kA\cos(\omega t+\phi )=0\;,$

which fixes $\omega ={\sqrt {k/m}}$. The quantity ω has dimension of frequency (1/time) and is often written as ω = 2π ν, where ν is the frequency (number of cycles per second) and ω is called angular frequency. The time T ≡ 1/ν is called the period of the cycle (duration of one cycle),

$T={\frac {1}{\nu }}={\frac {2\pi }{\omega }}=2\pi {\sqrt {\frac {m}{k}}}$

As stated, the amplitude and the phase angle φ are integration constants. Often it is possible to choose the zero of time such that ωt + φ = 0, implying that φ is zero:

$x(t)=A\cos({\sqrt {\frac {k}{m}}}t)=A\cos \omega t.$

The amplitude A is determined by how far we move initially (at t = 0) the mass (in figure 1) away from equilibrium

$x(0)=A\;$ .

From the form of the cosine function we know that x goes through zero (mass in equilibrium x = 0 in figure 1) at the following points in time:

$t_{0}={\frac {(2n+1)\,\pi }{2\omega }}\quad {\hbox{with}}\quad |n|=0,1,2,\ldots$

The displacement is minimum (mass in point x = −A in figure 1, i.e., furthest to the left) for the times

$t_{\mathrm {min} }={\frac {(2n+1)\,\pi }{\omega }}\quad {\hbox{with}}\quad |n|=0,1,2,\ldots$

The value of x is maximum (mass in point x = A in figure 1) for

$t_{\mathrm {max} }={\frac {2n\,\pi }{\omega }}\quad {\hbox{with}}\quad |n|=0,1,2,\ldots$

Note that for n = 0, t_min - t_max = π/ω = T/2 (the time of a half period). It takes time T for the mass to return to A.

The mass oscillates from x = A to x = −A and back again. The speed of the mass is

${\dot {x}}(t)=-A\omega \sin \omega t$,

which for the specific values of time is

${\begin{aligned}{\dot {x}}(t_{0})&=\pm A\omega &&({\hbox{maximum speed}})\\{\dot {x}}(t_{\mathrm {min} })&={\dot {x}}(t_{\mathrm {max} })=0&&{\hbox{(turning points)}}\\\end{aligned}}$

Physically, after the mass is displaced from equilibrium over a distance A to the right, the restoring force −kx pushes the mass back toward its equilibrium position, causing it to accelerate to the left. When it reaches equilibrium (x = 0), there is no force acting on it at that instant, but it is moving at maximum speed −Aω (to the left), and by Newton's first law it persists in its motion moving beyond equilibrium position. Before it is stopped it reaches position −A, and by this time there is a force acting on it again, pulling it back toward equilibrium (to the right in figure 1). The direction of the motion is turned around in the points x = ±A, which is why these are called turning points.

The whole process, known as simple harmonic motion, repeats itself endlessly with a period given by T = 2π √m/k. This relation means that the stiffer the springs (i.e., the larger k), the shorter the period (the faster the oscillations). Making the mass m greater has exactly the opposite effect, slowing the motion down.

One of the most important features of harmonic motion is the fact that the frequency of the motion (ω, T, or ν) depends only on the mass m and the stiffness k of the spring. It does not depend on the amplitude A of the motion. If the amplitude is increased, the mass moves faster, but the time required for a complete round trip (the argument of the cosine) remains the same. This fact is used in accurate timekeeping.

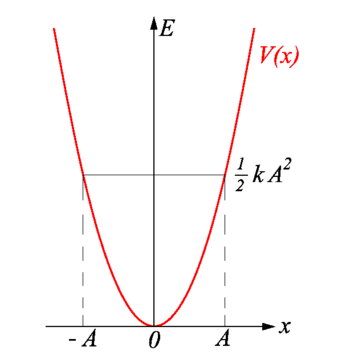
Harmonic potential

From classical mechanics it is known that the potential energy is minus the force integrated over distance:

$V(x)-V(x_{0})=\int _{x_{0}}^{x}\;ky\;\mathrm {d} y={\frac {1}{2}}kx^{2}-{\frac {1}{2}}kx_{0}^{2},$

where the zero of the potential is at the arbitrary point x₀ (the lower limit of the integral). When we choose x₀ = 0, we find V(x₀) = 0, so that V(x) = (k/2)x².

Introducing a minor generalization, we shift the origin on the x-axis from 0 to the arbitrary point x₀, i.e. we make the substitution x → x−x₀. Then the harmonic potential becomes the following quadratic function in the displacement x − x₀,

$V(x-x_{0})={\frac {1}{2}}k(x-x_{0})^{2}.$

It is of interest to show the connection with the Taylor expansion of an arbitrary potential around x₀

$V(x-x_{0})=V(x_{0})\;+\;(x-x_{0})\;\left[{\frac {dV(x)}{dx}}\right]_{x_{0}}\;+\;{\frac {1}{2}}\;(x-x_{0})^{2}\;\left[{\frac {d^{2}V(x)}{dx^{2}}}\right]_{x_{0}}\;+\cdots$

We truncate the expansion after these three terms. We take V(x₀) as zero of potential and assume that x₀ is a stationary point of the potential, i.e., that the potential at x₀ has a minimum, a maximum, or a point of inflection (saddle point). This means that we assume that

$\left[{\frac {dV(x)}{dx}}\right]_{x_{0}}=0.$

Then the truncated Taylor series shrinks to

$V(x-x_{0})={\frac {1}{2}}\;(x-x_{0})^{2}\;\left[{\frac {d^{2}V(x)}{dx^{2}}}\right]_{x_{0}}.$

If we identify Hooke's (spring) constant thus:

$k=\left[{\frac {d^{2}V(x)}{dx^{2}}}\right]_{x_{0}},$

we have found the harmonic potential from the truncated Taylor series. Note that since k > 0, the potential has a minimum at x₀ (the stationary point is a minimum).

We went from the force to the potential by integrating over distance. Conversely, given a potential V, it is known from classical mechanics that the corresponding force F is minus the derivative V',

$F=-V'=-(x-x_{0})\;\left[{\frac {dV(x)}{dx}}\right]_{x_{0}}=-(x-x_{0})\;k.$

So, one could say that we proved Hooke's law (force linear in displacement) by use of a truncated Taylor expansion.

Energy

E-x diagram. Vertical axis energy; horizontal axis displacement x. The potential energy V(x) = ½ kx² is shown in red.

The oscillating mass has kinetic plus potential energy:

$E={\frac {1}{2}}m{\dot {x}}(t)^{2}+{\frac {1}{2}}kx(t)^{2}$

Above we saw that

$x(t)=A\cos \omega t\quad {\hbox{and}}\quad {\dot {x}}(t)=-A\omega \sin \omega t$

so that

${\begin{aligned}E&={\frac {A^{2}}{2}}\left(m\omega ^{2}(\sin \omega t)^{2}+k(\cos \omega t)^{2}\right)\\&={\frac {A^{2}}{2}}\left(m{\Big (}{\frac {k}{m}}{\Big )}(\sin \omega t)^{2}+k(\cos \omega t)^{2}\right)\\&={\frac {kA^{2}}{2}}\end{aligned}}$

where we used ω² = k/m and cos² + sin² = 1. Hence, the total energy of the harmonic oscillator is constant (independent of time). It is quadratic in the amplitude A and proportional to the spring constant k. The stiffer the string the more energy.

During the oscillation the energy is converted from potential energy to kinetic energy and back. Consider the turning point x = A. We saw above that this point occurs for time t_max = 2πn / ω, and since sin(2πn) = 0, the velocity at this turning point is zero. Hence all energy ½k A² is potential energy at this point. The mass travels to the left and picks up speed and therewith kinetic energy. At the equilibrium point x = 0 we have V(x) = 0 and all energy ½k A² is turned into kinetic energy. The mass loses speed and comes to a momentary standstill at the left turning point x = −A, where again all energy is converted into potential energy.