CZ:Featured article/Current

In electronics, the Miller effect is the increase in the equivalent input capacitance of an inverting voltage amplifier due to a capacitance connected between two gain-related nodes, one on the input side of an amplifier and the other the output side. The amplified input capacitance due to the Miller effect, called the Miller capacitance C_M, is given by

$C_{M}=C(1-A)\ ,$

where A is the voltage gain between the two nodes at either end of the coupling capacitance, which is a negative number because the amplifier is inverting, and C is the coupling capacitance.

Although the term Miller effect normally refers to capacitance, the Miller effect applies to any impedance connected between two nodes exhibiting gain. These properties of the Miller effect are generalized in Miller's theorem.

The Miller effect is named after John Milton Miller.When Miller published his work in 1920, he was working on vacuum tube triodes, however the same theory applies to more modern devices such as bipolar transistors and MOSFETs.

Derivation

(PD) Image: John R. Brews
These two circuits are equivalent. Arrows indicate current flow. Notice the polarity of the dependent voltage source is flipped, to correspond with an inverting amplifier.

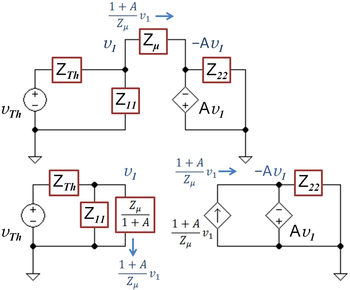
Consider a voltage amplifier of gain −A with an impedance Z_μ connected between its input and output stages. The input signal is provided by a Thévenin voltage source representing the driving stage. The voltage at the input end (node 1) of the coupling impedance is v₁, and at the output end −Av₁. The current through Z_μ according to Ohm's law is given by:

$i_{Z}={\frac {v_{1}-(-A)v_{1}}{Z_{\mu }}}={\frac {v_{1}}{Z_{\mu }/(1+A)}}$.

The input current is:

$i_{1}=i_{Z}+{\frac {v_{1}}{Z_{11}}}\ .$

The impedance of the circuit at node 1 is:

${\frac {1}{Z_{1}}}={\frac {i_{1}}{v_{1}}}={\frac {1+A}{Z_{\mu }}}+{\frac {1}{Z_{11}}}.$

This same input impedance is found if the input stage simply is decoupled from the output stage, and the reduced impedance Z_μ / (1+A) is substituted in parallel with Z₁₁. Of course, if the input stage is decoupled, no current reaches the output stage. To fix that problem, a dependent current source is attached to the second stage to provide the correct current to the output circuit, as shown in the lower figure. This decoupling scenario is the basis for Miller's theorem, which replaces the current source on the output side by addition of a shunt impedance in the output circuit that draws the same current. The striking prediction that a coupling impedance Z_μ reduces input impedance by an amount equivalent to shunting the input with the reduced impedance Z_μ / (1+A) is called the Miller effect.

...