Legendre-Gauss Quadrature formula
Legendre-Gauss Quadratude formiula is the approximation of the integral
- (1)
with special choice of nodes and weights , characterised in that, if the finction is polynomial of order smallet than , then the exact equality takes place in equation (1).
Legendre-Gauss quadratude formula is special case of Gaussian quadratures of more general kind, which allow efficient approximation of a function with known asumptiotic behavior at the edges of the interval of integration.
Nodes and weights
Nodes in equation (1) are zeros of the Polynomial of Legendre :
- (2)
- (3)
Weight in equaiton (1) can be expressed with
- (4)
There is no straightforward espression for the nodes ; they can be approximated with many decimal digits through only few iterations, solving numerically equation (2) with initial approach
- (5)
These formulas are described in the books [1] [2]
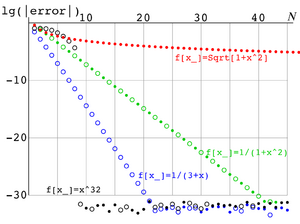
Precision of the approximation
Example
Extension to other interval
is straightforward. Should I copypast the obvious formulas here?
References
- ↑ Abramovitz, Milton; I. Stegun (1964). Handbook of mathematical functions. National Bureau of Standards. ISBN 0-486-61272-4.
- ↑ W.H.Press, S.A.Teukolsky, W.T.Vetterling, B.P.Flannery (1988). Numerical Resipes in C. Cambridge University Press.