Factorial

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n}	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n!}
0	1
1	1
2	2
3	6
4	24
5	120
6	720
7	5040
8	40320
9	362880
10	3628800

In mathematics, the factorial is the meromorphic function with fast growth along the real axis; for non-negative integer values of the argument, this function has integer values. Frequently, the postfix notation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n!} is used for the factorial of number Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} . For integer Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} , the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n!} gives the number of ways in which n labelled objects (for example the numbers from 1 to n) can be arranged in order. These are the permutations of the set of objects. In some programming languages, both n! and factorial(n) , or Factorial(n), are recognized as the factorial of the number Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} .

Integer values of the argument

For integer values of the argument, the factorial can be defined by a recurrence relation. If n labelled objects have to be assigned to n places, then the n-th object can be placed in one of n places: the remaining n-1 objects then have to be placed in the remaining n-1 places, and this is the same problem for the smaller set. So we have

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n! = n \cdot (n-1)! \,}

and it follows that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n! = n \cdot (n-1) \cdots 2 \cdot 1 , \,}

which we could derive directly by noting that the first element can be placed in n ways, the second in n-1 ways, and so on until the last element can be placed in only one remaining way.

Since zero objects can be arranged in just one way ("do nothing") it is conventional to put 0! = 1.

The factorial function is found in many combinatorial counting problems. For example, the binomial coefficients, which count the number of subsets size r drawn from a set of n objects, can be expressed as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \binom{n}{r} = \frac{n!}{r! (n-r)!} .}

The factorial function can be extended to arguments other than positive integers: this gives rise to the Gamma function.

Definitions

For complex values of the argument, the combinatoric definiton above should be extended. The factorial can be defined as unique meromorphic function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F} , satisfying relations

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(z+1)=(z+1) F(z) }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(0)=1 }

for all complex Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} except negative integer values. This definition is not constructive, and gives no straightforward way for the evaluation. Therefore, the integral representation is used as definition. For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Re(z)>-1} , define

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z! = \int_0^\infty t^z \exp(-t) \mathrm{d}t }

Such definition is similar to that of the Gamma function, and leads to the relation

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z!=\Gamma(z+1)}

for all complex Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} except the negative integer values.

The definition above agrees with the combinatoric definition for integer values of the argument; at integer Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} , the integral can be expressed in terms of the elementary functions.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f=z!} in the complex Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} -plane.

The definition through the integral can be extended to the whole complex plane, using relation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z!=(z+1)!/(z+1)} for the cases Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Re(z)<-1} , assuming that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} 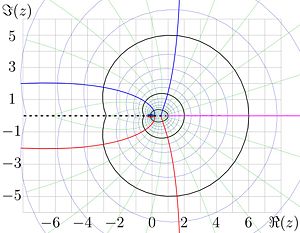in not negative integer. This allows to plot the map of factorial in the complex plane. In the figure, lines of constant Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u=\Re(z!)} and lines of constant Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v=\Im(z!)} are shown.
The levels u = − 24, − 20, − 16, − 12, − 8, − 7, − 6, − 5, − 4, − 3, − 2, − 1,0,1,2,3,4,5,6,7,8,12,16,20,24 are drown with thick black lines.
Some of intermediate levels u = const are shown with thin blue lines for positive values and with thin red lines for negative values.
The levels v = − 24, − 20, − 16, − 12, − 8, − 7, − 6, − 5, − 4, − 3, − 2, − 1 are shown with thick red lines.
The level v = 0 is shown with thick pink lines.
The levels v = 1,2,3,4,5,6,7,8,12,16,20,24 are drown with thick blue lines. some of intermediate levels v = const are shown with thin green lines.
The dashed blue line shows the level Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u=\mu_0} and corresponds to the value Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_0=(x_0)!\approx 0.85} of the principal local minimum Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0\approx 0.45} of the factorial of the real argument.
The dashed red line shows the level and corresponds to the similar value of the negative local extremum of the factorial of the real argument.
Due to the fast growth of the function, in the right hand side of the figure, the density of the levels exceeds the ability of the plotter to draw them; so, this part is left empty.

Factorial of the real argument

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{factorial}(x)=x!} ; the inverse function, id est, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{factorial}^{-1}(x)} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{factorial}(x)^{-1}} versus real Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} .

The definition above was elaborated for factorial of complex argument. In particular, it can be used to evlauate the factorial of the real argument. In the figure at right, the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{factorial}(x)=x!} is plotted versus real Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} with red line. The function has simple poluses at negative integer Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} .

At Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x\rightarrow -1+o} , the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x! \rightarrow +\infty} .

The local minimum

The factorial has local minimum at

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=\nu_0\approx 0.461632144968362341262659542325721328468196204}

marked in the picture with pink vertical line; at this point, the derivative of the factorial is zero:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{factorial}^{\prime}(\nu_0)=0}

The value of factorial in this point

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_0=\nu_0!=\mathrm{factorial(\nu_0)}\approx 0.88560319441088870027881590058258873320795153367}

The Tailor expansion of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z!} at the point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=\nu_0} can be writen ax follows:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z!=\mu_0+\sum_{n=2}^{N-1} c_n (z-\nu_0)^n + \mathcal{O}(z-\nu_0)^N}

The approximations for the coefficients of this expansion are in the table:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n}	approximation of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_n}
2	0.428486815855585429730209907810650582960483696962
3	-0.130704158939785761928008749242671025181542078103
4	0.160890753325112844190519489594363387594505844657
5	-0.092277030213334350126864106458600575084335085690

This expansion can be used for the precise evaluation of the inverse function of factorial (arcfactorial) in vicinity of the branchpoint.

Other local extremums are at negative values of the argument; one of them in shown in the figure above.

Specific values

For several specific values of the argument, the simple representations for the factorial are known. In addition fo the integer values, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(-\frac{1}{2}\right)!=\sqrt{\pi}} ; then, using the relationFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z!=z\cdot(z+1)!} , values at half-integer argument can be expressed; for example, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\frac{1}{2}\right)!=\frac{\sqrt{\pi}}{2}\approx 0.8862269255} is slightly greater than Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_0} , which is minimal value of this function for the positive values of the argument.

Values of factorial at integer plus quarter and at integer plut third are mentioned in in textbooks, but these valeus do not have special notations.

Related functions

In the figure above, the two other functions are plotted. The first of them is

$\mathrm {ArcFactorial} (x)=\mathrm {factorial} ^{-1}(x)$

is the inverse function;

$\mathrm {factorial} {\Big (}\mathrm {ArcFactorial} (x){\Big )}=x~\forall x>\mu _{0}$

In the range of biholomorphism, the inverse relation is also valid; in particular,

$\mathrm {ArcFactorial} {\Big (}\mathrm {factorial} (x){\Big )}=x~\forall x>\nu _{0}$

Specific values of the inverse function:

$\mathrm {ArcFactorial} (\mu _{0})=\nu _{0}$,

$\mathrm {ArcFactorial} \left({\frac {\sqrt {\pi }}{2}}\right)={\frac {1}{2}}$,

$\mathrm {ArcFactorial} \left(1\right)=1$,

$\mathrm {ArcFactorial} \left(2\right)=2$,

$\mathrm {ArcFactorial} \left(6\right)=3$.

For comparison, in the figure above, the function

$f(x)=\mathrm {factorial} (x)^{-1}=(x!)^{-1}={\frac {1}{x!}}$

is plotted with the blue curve. This function is entire, id est, it has no singularities, and can used for the approximation of factorial. The Tailor series for this function always converge (this function has has infinite radius of convergence).

Inverse function

ArcFactorial in the complex plane.

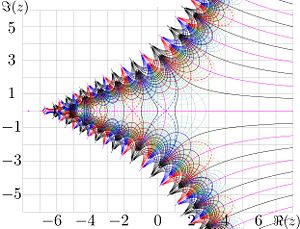
Inverse function of factorial can be defined with equation

$(\mathrm {ArcFactorial} (z))!=z$

and condition that ArcFactorial is holomorphic in the comlex plane with cut along the part of the real axis, that begins at the minimum of factorial of the real argument and extends to $-\infty$. This function is shown with lines of constant real part $u=\Re (\mathrm {ArcFactorial} (z))$ and lines of constant imaginary part $v=\Im (\mathrm {ArcFactorial} (z))$.

Levels $u=1,2,3$ are shown with thick black curves.
Levels $u=0.2,0.4,0.6,0.8,1.2,1.4,1.6,1.8,2.2,2.4,2.6,2.8,3.2,3.4,3.6$ are shown with thin blue curves.
Levels $v=1,2,3$ are shown with thick blue curves.
Level $v=0$ is shown with thick pink line.
Levels $v=-1,-2,-3$ are shown with thick red curves.
The intermediate levels of constant $v$ are shown with thin dark green curves.

The ArcFactorial has the branch point $\mu _{0}\approx 0.85$; the cut of the range of holomorphizm is shown with black dashed line.

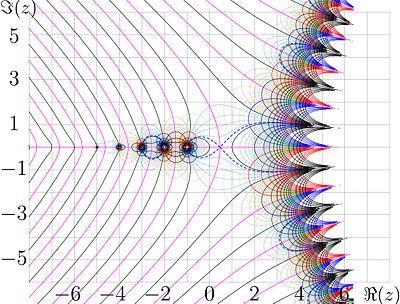
The figure shows the mapping ot the complex plane with the factorial function. In particular, factorial maps the unity to unity; two is mapped to two, and 3 is mapped to 6.

Function $f(z)=1/z!$

$f(z)={\frac {1}{z!}}$ in the complex $z$-plane.

The inverse function of factorial, id est, $\mathrm {ArcFactorial} (z)=\mathrm {Factorial} ^{-1}(z)$ from the previous section, sohuld not be confused with $f(z)={\frac {1}{z!}}=\mathrm {Factorial} (z)^{-1}={\frac {1}{\mathrm {Factorial} (z)}}$ shown in the figure at right. The lines of constant $u=\Re (f(z))$ and the lines of constant $v=\Im (f(z))$ are drawn.
The levels $u=-24,-20,-16,-12,-8,-7..7,8,12,16,20,24$ are shown with thick black lines.
The levels $v=-24,-20,-16,-12,-8,-7...7,-1$ are shown with thick red lines.
The level $v=0$ is shown with thick pink line.
The levels $v=1,2,...7,8,12,16,20,24$ are shown with thick blue lines.
Some of intermediate elvels $u=$const are shown with thin red lines for negative values and thin blue lines for the positive values.
Some of intermediate elvels $v=$const are shown with thin green lines.
The blue dashed curves represent the level $u=1/\mu _{0}$ and correspond to the positive local maximum of the inverse function of the real argument.
The red dashed curves represent the level $u=1/\mu _{1}$, which corresponds to the first negative local maximum of the factorial of the real argument; $\mathrm {factorial} ^{\prime }(\nu _{1})=0$; $\mathrm {factorial} (\nu _{1})=\mu _{1}$.

$f(z)={\frac {1}{z!}}$ is entire function, that grows in the left hand side of the compelx plane and quickly decays to zero along the real axis.

Evaluation of the factorial

In principle, the integral representation from the definition above can be used for the evlauation of the factorial. However, such an implementation is not efficient, and is not suitable, when the factorial is used as a component in construction of other functions with complicated representations that involve many evaluations of the factorial. Therefore, the approximations with elementary functions are used.

Historically, one of the first approximations of the factorial with elementary funcitons was the Stirling formula below.

Stirling's formula

For large n there is an approximation due to Scottish mathematician James Stirling

$n!\approx {\sqrt {2\pi }}n^{n+1/2}e^{-n}.\,$

References

• Ronald L. Graham; Donald E. Knuth, Oren Patashnik (1989). Concrete Mathematics. Addison Wesley, 111,332. ISBN 0-201-14236-8.