Pi (mathematical constant)

Area of the circle = π × area of the shaded square

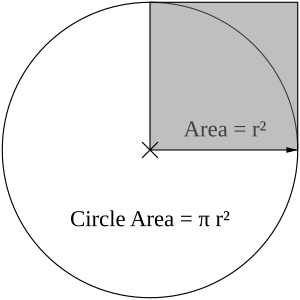
Pi, denoted by the Greek letter π, is a mathematical constant with the approximate value 3.14159. In Euclidean geometry, π represents the proportion between the circumference and the diameter of any circle, or equivalently, the proportion between a circle's area and the square of its radius. This proportion is also found in many other geometrical objects, such as spheres and cones. Pi has further uses in many other areas of mathematics.

Pi is an irrational number, which means that it cannot be expressed exactly as a ratio of integers, and transcendental, meaning that it does not satisfy any algebraic equation. Since it is irrational, π cannot be written as a finite or periodically repeating decimal. The first 50 digits after the decimal point are

3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 ...

Early geometrical study

The fact that the ratio of the circumference to the diameter of a circle is the same for all circles, and that it is slightly more than 3, was known to ancient Egyptian, Babylonian, Indian and Greek geometers. Preserved documents do not refer to the number explicitly, but contain approximations for π as part of methods for calculating circumference or area. A Babylonian stone tablet from 1900 BC uses the proportion 25/8 = 3.125, and an Egyptian document from the same time gives the ratio (16/9)² ≈ 3.16. The ancient Indian text Shatapatha Brahmana gives π as 339/108 ≈ 3.139. All of these values differ from the true value by less than one percent. The Books of Kings (600 BC) appears to suggest π = 3, which is notably worse than other estimates available at the time, although it is disputed whether the text suggests an exact value.

Archimedes (287–212 BC), in whose honor π is sometimes called Archimedes' constant, was the first to treat the number with mathematical rigor. He knew how to calculate the circumference of a regular polygon, and realized that a polygon inscribed in a circle has a smaller circumference than the circle whereas a circumscribed polygon has a greater circumference. By calculating the circumferences of two 96-sided polygons, one slightly smaller than a unit circle and the other slightly larger, he rigorously proved the bounds 223/71 < π < 22/7. Taking the average of the bounds yields the approximation π ≈ 3.1419. The method of Archimedes is the first known algorithm for calculating π with arbitrary accuracy.

In the following centuries, most significant mathematical development took place in India and China. Around 480, the Chinese mathematician Zu Chongzhi gave the approximation π = 355/113, and showed that 3.1415926 < π < 3.1415927, which would stand as the most accurate value for π over the next 900 years.

References

• Jonathan Borwein & David Bailey (2003). Mathematics by Experiment - Plausible Reasoning in the 21st Century. ISBN 1-56881-211-6