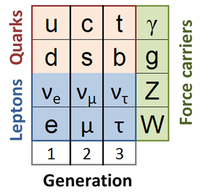
Standard Model

(PD) Image: John R. Brews
The fundamental particles and messenger quanta of the Standard Model.

The Standard Model of particle physics is the mathematical theory that describes the weak, electromagnetic and strong interactions between leptons and quarks, the basic particles of particle physics. This model is very strongly supported by experimental observations, and is considered to be a major achievement (perhaps the most outstanding achievement) of theoretical physics. It does not, however, treat the gravitational force, inclusion of which remains an elusive goal of the ultimate "theory of everything". The Standard Model is accordingly not consistent with general relativity. The theory is consistent with special relativity.

The model is described only qualitatively in this article, and neither mathematical details nor experimental phenomenology are provided. The objective here is only an introduction to the basic terminology for particles in the Standard Model and their interactions.

Particles and interactions

The interactions between the particles of the Standard Model are well known experimentally, and transcend the Standard Model. However, the particles of the Standard Model are introduced with the ways that they use these interactions to assemble a complete theory of the interactions between various manifestations of matter. The fundamental particles are spin 1/2 fermions of two types: leptons and quarks. Their interactions are viewed as exchange forces, which is to say the forces are introduced by the trading back and forth of force carriers, different kinds of particle that represent quanta of the underlying force fields. So, for example, the quanta of the electromagnetic field are photons. The strength of an electromagnetic field is dictated by the number of photons that make it up, and the exchange of photons between particles with electric charge is the mechanism underlying the field's ability to exert an electromagnetic force upon these bodies.

Leptons

Leptons are one type of fundamental particle. They have spin 1/2 and are not subject to the strong force. The known leptons are said to be of three families or generations (labeled in the table as 1, 2, 3) and of six flavors, a generic term for the particle names. They are listed in the table below. Their antiparticles also are leptons with opposite electric charge Q and opposite Lepton number L_e,μ,τ.

Lepton flavor properties

Particle name	Symbol	Family/Generation	Q (e)	Le	Lμ	Lτ	Mass (MeV)	Lifetime (s)
Electron	e−	1	−1	+1	0	0	0.510 998 928(11)	Stable
Muon	μ−	2	−1	0	+1	0	105.658 3715(35)	2.197019(21) × 10−6
Tau	τ−	3	−1	0	0	+1	1776.82(16)	2.906(10) × 10-13
Electron neutrino	νe	1	0	+1	0	0	< 225 × 10−6	Unknown
Muon neutrino	νμ	2	0	0	+1	0	< 0.19	Unknown
Tau neutrino	ντ	3	0	0	0	+1	< 18.2	Unknown

Quarks

Quarks are a type of particle with spin 1/2 that are subject to strong, weak and electromagnetic forces. The known quarks are listed in the table below. The kinds of quark (u, d, c, s, t, d) are referred to as the flavor index of the quark, and besides a flavor index, each quark has a color index, which may be any of three colors: red, green and blue (r, g, b). Their antiparticles also are quarks, but carry anti-colors: anti-red, anti-green, anti-blue. Unlike a particle's electric charge, which can be any multiple of the elementary charge e, a quark can carry only one unit of color. The elementary unit of color has not been measured, a result of failure to observe an isolated quark.

Quark flavor properties

Name	Symbol	Family/Generation	B	Q(e)	I3	C	S	T	B′	Mass (MeV)	Antiparticle	Antiparticle symbol
Up	u	1	+1/3	+2/3	+1/2	0	0	0	0	2.34 ± 0.19	Antiup	ū
Down	d	1	+1/3	−1/3	−1/2	0	0	0	0	4.78 ± 0.11	Antidown	${\overline {d}}$
Charm	c	2	+1/3	+2/3	0	+1	0	0	0	1.294 ± 0.004 × 103	Anticharm	${\overline {c}}$
Strange	s	2	+1/3	−1/3	0	0	−1	0	0	100.2 ± 2.4	Antistrange	${\overline {s}}$
Top	t	3	+1/3	+2/3	0	0	0	+1	0	172.9 ±0.6 ±0.9 × 103	Antitop	${\overline {t}}$
Bottom	b	3	+1/3	−1/3	0	0	0	0	−1	4.19 (+0.18) (−0.06) × 103	Antibottom	${\overline {b}}$

B = baryon number, Q = electric charge, I₃ = isospin, C = charm, S = strangeness, T = topness, B′ = bottomness.
* Notation such as ±xxx denotes measurement uncertainty. In the case of the top quark, the first uncertainty is statistical in nature, and the second is systematic.

The quarks carry fractional electric charge. However, no quark has been observed in isolation, so a "free" fractional electric charge has not been seen.

Quanta

Because gravitation is not included in the standard model, there are three type of interaction included. Each type of interaction is mediated by exchange of quanta that are bosons, sometimes called messenger particles.

Messenger particles

Interaction field	Particle name	Symbol	Spin	Range (m)	Mass(GeV)
Electromagnetic field	Photon	γ	1	∞	< 10−27
Weak field	Weak bosons	W+, W−, Z	1	≈ 10−17	MW=80.399±0.023; MZ=91.1876±0.0021
Strong field	Gluons (8)	g	1	≈ 10−15	0

Photons

The photon mediates the electromagnetic force and has a very long history. It has neither electric charge nor mass.

Weak gauge bosons

The massive W⁺, W⁻, Z, weak bosons are the messenger particles for the weak force. Their nonzero mass is expected from the Standard Model because of the introduction of the Higgs boson, a particle yet to be seen experimentally, and conjectured to have a mass as large as 1000 GeV. The W⁺, W⁻ are antiparticles of each other and the Z boson is its own antiparticle.

Gluons

Gluons mediate the strong force as an exchange force due to color, one property of quarks. A gluon carries both a color and an anti-color. When a quark emits a gluon, its color changes in a way dependent upon the color/anti-color of the emitted gluon. For example, a red quark can emit a red-antiblue gluon, becoming a blue quark. There are nine possible color-anticolor combinations of r, g, b, which leads to only eight possible gluons because emission by a quark of one color-anticolor combination $(r{\overline {r}}+g{\overline {g}}+b{\overline {b}})/{\sqrt {3}}$ doesn't change the state of a quark and cannot act as a messenger. The remaining eight gluon color combinations are shown below.

Gluon color combinations

$r{\overline {g}}$	$g{\overline {b}}$	$b{\overline {r}}$	${\frac {1}{\sqrt {6}}}\left(r{\overline {r}}+g{\overline {g}}-2b{\overline {b}}\right)$
$g{\overline {r}}$	$b{\overline {g}}$	$r{\overline {b}}$	${\frac {1}{\sqrt {2}}}\left(r{\overline {r}}-g{\overline {g}}\right)$

The peculiar combinations: $(r{\overline {r}}+g{\overline {g}}+b{\overline {b}})/{\sqrt {3}}\ ,$, $\left(r{\overline {r}}-g{\overline {g}}\right)/{\sqrt {2}}\ ,$,  $\left(r{\overline {r}}+g{\overline {g}}-2b{\overline {b}}\right)/{\sqrt {6}}\ ,$  result from arranging all the possible combinations of colors and anti-colors as symmetrized unit vectors in a space of color/anti-color products.

Nuclear forces and mesons

(PD) Image: John R. Brews
A neutron and proton trade identities by exchange of a π⁻ in the Yukawa model.

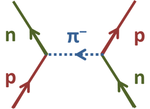
In 1935 Yukawa invented the meson theory for explaining the forces holding atomic nucleii together, an assemblage of neutrons and protons. The mesons were postulated to exist in three forms: π⁺,π⁰, and π^– , all of spin zero, today called pions. Incidental experimental observation of the muon or μ-meson in 1936 appeared to provide the π^– meson needed by the theory, but soon it was found that the muon did not interact with the nucleus and had spin 1/2 (it is a lepton). Later, in 1947, the actual π-meson or pion was discovered, and the pion did interact with the nucleus. Today all three pions have been observed, π⁺,π⁰, and π^–, the last observed being the neutral pion found in 1950. The behavior of nuclear forces was explained as an exchange of pions. An example is shown in the figure, where the neutron (lower right) emits a pion of negative electric charge to become a positive proton (upper right), while the proton (lower left) absorbs the pion to become a neutron (upper left). Today, pions are considered to be quark-antiquark pairs, and a more refined theory of nuclear interactions is based upon the Standard Model. Nuclear forces are not considered fundamental today, but are a consequence of the underlying strong forces between quarks, also called chromodynamic forces or color forces. On that basis, nuclear forces are an exchange force fundamentally based upon color, and only approximated by the Yukawa theory.