Clausius-Mossotti relation: Difference between revisions
imported>Paul Wormer No edit summary |
imported>Paul Wormer No edit summary |
||
| Line 1: | Line 1: | ||
{{subpages}} | |||
The '''Clausius-Mossotti relation''' <ref> | The '''Clausius-Mossotti relation''' <ref> | ||
O.F. Mossotti, Memorie Mat. Fis. Modena vol. '''24''', p. 49 (1850). | O.F. Mossotti, Memorie Mat. Fis. Modena vol. '''24''', p. 49 (1850).</ref><ref> | ||
R. Clausius, Die mechanische Wärmetheorie II 62 Braunschweig (1897). </ref> connects the [[relative permittivity]] ε<sub>r</sub> of a [[dielectric]] to the [[polarizability]] α of the molecules constituting | R. Clausius, Die mechanische Wärmetheorie II 62 Braunschweig (1897). </ref> connects the [[relative permittivity]] ε<sub>r</sub> of a [[dielectric]] to the [[polarizability]] α of the atoms or molecules constituting the dielectric. The relative permittivity is a bulk (macroscopic) property and polarizability is a microscopic property of matter. | ||
The relation for dielectric matter consisting of atoms or ''non-polar'' molecules is | |||
:<math> | |||
\frac{\epsilon_r -1}{\epsilon_r+2} = \frac{1}{3\epsilon_0} N \alpha, | |||
</math> | |||
where ε<sub>0</sub> is the [[electric constant]] (permittivity of the vacuum) and ''N'' is the number density (number of atoms or molecules per volume). | |||
''' | The [[index of refraction]] ''n'' of a dielectric is given by | ||
:<math> | |||
n = \sqrt{\epsilon_r \mu_r} \approx \sqrt{\epsilon_r}, | |||
</math> | |||
where we used that for most dielectric matter the relative [[magnetic permeability]] μ<sub>r</sub> is very close to unity. Substitution of this value of ''n'' gives the [[Lorentz-Lorenz relation]] | |||
:<math> | |||
\frac{n^2 -1}{n^2+2} = \frac{1}{3\epsilon_0} N \alpha. | |||
</math> | |||
==Derivation== | |||
Consider ''N'' atoms or molecules, constituting the dielectric, in an external [[electric field]] '''E'''. The sum of this field and an internal field '''E'''<sub>int</sub> induces a dipole '''p'''<sub>ind</sub> on each molecule. The polarization vector '''P''' is the sum of the induced dipoles, | |||
:<math> | |||
\mathbf{P} = N \mathbf{p}_\mathrm{ind}. | |||
</math> | |||
From the relation between '''P''', the [[electric displacement]], and the electric field | |||
follows | |||
:<math> | |||
\mathbf{P} = \epsilon_0(\epsilon_r-1) \mathbf{E}. | |||
</math> | |||
To get an expression for '''p'''<sub>ind</sub>, we consider a single molecule in a little spherical cavity inside the dielectric. It is shown below that the total field inside this cavity is | |||
:<math> | |||
E_\mathrm{tot} = E + E_\mathrm{int} = E + \frac{1}{3\epsilon_0} P, | |||
</math> | |||
where we introduced absolute magnitudes, which is allowed because all vectors lie along the ''z''-axis, the direction of '''E'''. Now, | |||
:<math> | |||
p_\mathbf{ind} =\alpha E_\mathrm{tot} = \alpha (E + \frac{1}{3\epsilon_0} P). | |||
</math> | |||
Further, | |||
:<math> | |||
P = \epsilon_0(\epsilon_r-1) E = N\alpha (E + \frac{1}{3}(\epsilon_r-1)E) | |||
\quad\Longrightarrow \quad | |||
\epsilon_0(\epsilon_r-1) = \frac{N\alpha}{3} (3 +\epsilon_r-1), | |||
</math> | |||
from which the Clausius-Mossotti relation follows directly. | |||
We neglected here the contributions to the total field in the cavity from the other molecules in the cavity. It can be shown that these contributions average out in most dielectrics. | |||
==Internal electric field in dielectric== | ==Internal electric field in dielectric== | ||
Revision as of 06:01, 10 December 2008
The Clausius-Mossotti relation [1][2] connects the relative permittivity εr of a dielectric to the polarizability α of the atoms or molecules constituting the dielectric. The relative permittivity is a bulk (macroscopic) property and polarizability is a microscopic property of matter. The relation for dielectric matter consisting of atoms or non-polar molecules is
where ε0 is the electric constant (permittivity of the vacuum) and N is the number density (number of atoms or molecules per volume).
The index of refraction n of a dielectric is given by
where we used that for most dielectric matter the relative magnetic permeability μr is very close to unity. Substitution of this value of n gives the Lorentz-Lorenz relation
Derivation
Consider N atoms or molecules, constituting the dielectric, in an external electric field E. The sum of this field and an internal field Eint induces a dipole pind on each molecule. The polarization vector P is the sum of the induced dipoles,
From the relation between P, the electric displacement, and the electric field follows
To get an expression for pind, we consider a single molecule in a little spherical cavity inside the dielectric. It is shown below that the total field inside this cavity is
where we introduced absolute magnitudes, which is allowed because all vectors lie along the z-axis, the direction of E. Now,
Further,
from which the Clausius-Mossotti relation follows directly.
We neglected here the contributions to the total field in the cavity from the other molecules in the cavity. It can be shown that these contributions average out in most dielectrics.
Internal electric field in dielectric
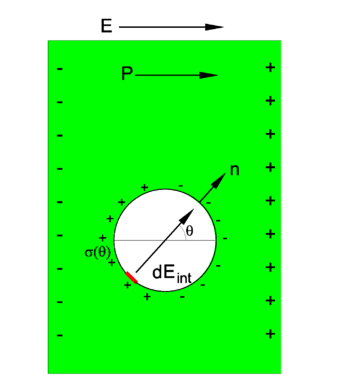
A macroscopic slab of dielectric is placed in an outer electric field E (the z-direction) that polarizes the dielectric, so that a surface charge density σp is created. Since E "pushes" positive charge and "pulls" negative charge, the sign of the charge density on the outer surface is as is indicated in the figure. The polarization vector P points by definition from negative to positive charge. The surface charge density σp is in absolute value equal to |P|.
An infinitesimally small spherical cavity of radius r is made in the dielectric and inside this cavity there is vacuum with permittivity (electric constant) ε0. Because of electric neutrality the surface of the cavity has the charge density (in absolute value),
where n is a unit length vector perpendicular to the surface of the cavity at the point θ. By definition, the positive direction of the normal n is outward.
An infinitesimal element on the surface of the cavity gives a contribution to the internal electric field Eint parallel to n,
The z-component of this contribution to the field is
Integration over the whole surface gives
The total electric field in the cavity is in the z direction and has magnitude