Reflection (geometry)

In Euclidean geometry, a reflection is a linear operation σ on $\mathbb {R} ^{3}$ with σ² = E, the identity map. This property of σ is called involution. An involutory operator is non-singular and σ⁻¹ = σ. Reflecting twice an arbitrary vector brings back the original vector :

$\sigma ({\vec {\mathbf {r} }}\,)={\vec {\mathbf {r} }}\,'\quad {\hbox{and}}\quad \sigma ({\vec {\mathbf {r} }}\,'\,)={\vec {\mathbf {r} }}.$

The operation σ is an isometry of $\mathbb {R} ^{3}$ onto itself, which means that it preserves inner products and that its inverse is equal to its adjoint,

$\sigma ^{\mathrm {T} }=\sigma ^{-1}\;(=\sigma ).\,$

Hence reflection is also symmetric: σ^T = σ. From (det(σ))² = det(E) = 1 follows that isometries have determinant ±1. Those with positive determinant are rotations, while reflections have determinant −1. Because σ is symmetric it has real eigenvalues; since the extension of an isometry to a complex space is unitary, its (complex) eigenvalues have modulus 1. It follows that the eigenvalues of σ are ±1. The product of the eigenvalues being its determinant, −1, the sets of eigenvalues of σ are either {1, 1, −1}, or {−1, −1, −1}. An operator with the latter set of eigenvalues is equal to −E, minus the identity operator. This operator is known alternatively as inversion, reflection in a point, or parity operator. An operator with the former set of eigenvalues is reflection in a plane. Reflections in a plane are the subject of this article. Sometimes one finds the concept of "reflections in a line", these are rotations over 180°, see rotation matrix.

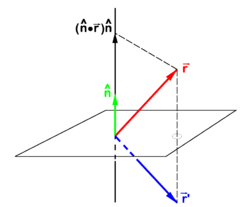
PD Image
Fig. 1. The vector $\scriptstyle {\vec {\mathbf {r} }}$ goes to $\scriptstyle {\vec {\mathbf {r} }}'$ under reflection in a plane. The unit vector $\scriptstyle {\hat {\mathbf {n} }}$ is normal to mirror plane.

Reflection in a plane

If ${\hat {\mathbf {n} }}$ is a unit vector normal (perpendicular) to a plane—the mirror plane—then $({\hat {\mathbf {n} }}\cdot {\vec {\mathbf {r} }}){\hat {\mathbf {n} }}$ is the projection of ${\vec {\mathbf {r} }}$ on this unit vector. From the figure it is evident that

${\vec {\mathbf {r} }}-{\vec {\mathbf {r} }}\,'=2({\hat {\mathbf {n} }}\cdot {\vec {\mathbf {r} }})\,{\hat {\mathbf {n} }}\;\Longrightarrow \;{\vec {\mathbf {r} }}\,'={\vec {\mathbf {r} }}-2({\hat {\mathbf {n} }}\cdot {\vec {\mathbf {r} }}){\hat {\mathbf {n} }}$

If a non-unit normal ${\vec {\mathbf {n} }}$ is used then substitution of

${\hat {\mathbf {n} }}={\frac {\vec {\mathbf {n} }}{|{\vec {\mathbf {n} }}|}}\equiv {\frac {\vec {\mathbf {n} }}{n}}$

gives the mirror image,

${\vec {\mathbf {r} }}\,'={\vec {\mathbf {r} }}-2{\frac {({\vec {\mathbf {n} }}\cdot {\vec {\mathbf {r} }}){\vec {\mathbf {n} }}}{n^{2}}}$

Sometimes it is convenient to write this as a matrix equation. Introducing the dyadic product, we obtain

${\vec {\mathbf {r} }}\,'=\left[\mathbf {E} -{\frac {2}{n^{2}}}{\vec {\mathbf {n} }}\otimes {\vec {\mathbf {n} }}\right]\;{\vec {\mathbf {r} }},$

where E is the 3×3 identity matrix.

Dyadic products satisfy the matrix multiplication rule

$[{\vec {\mathbf {a} }}\otimes {\vec {\mathbf {b} }}]\,[{\vec {\mathbf {c} }}\otimes {\vec {\mathbf {d} }}]=({\vec {\mathbf {b} }}\cdot {\vec {\mathbf {c} }}){\big (}{\vec {\mathbf {a} }}\otimes {\vec {\mathbf {d} }}{\big )}.$

By the use of this rule it is easily shown that

$\left[\mathbf {E} -{\frac {2}{n^{2}}}{\vec {\mathbf {n} }}\otimes {\vec {\mathbf {n} }}\right]^{2}=\mathbf {E} ,$

which confirms that reflection is involutory.

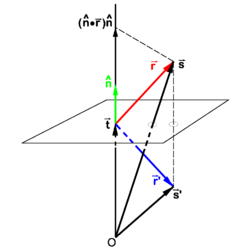
PD Image
Fig. 2. The vector ${\vec {\mathbf {s} }}$ goes to ${\vec {\mathbf {s} }}\,'$ under reflection

Reflection in a plane not through the origin

In Figure 2 a plane, not containing the origin O, is considered that is orthogonal to the vector ${\vec {\mathbf {t} }}$. The length of this vector is the distance from O to the plane. From Figure 2, we find

${\vec {\mathbf {r} }}={\vec {\mathbf {s} }}-{\vec {\mathbf {t} }},\quad {\vec {\mathbf {r} }}\,'={\vec {\mathbf {s} }}\,'-{\vec {\mathbf {t} }}$

Use of the equation derived earlier gives

${\vec {\mathbf {s} }}\,'-{\vec {\mathbf {t} }}={\vec {\mathbf {s} }}-{\vec {\mathbf {t} }}-2{\big (}{\hat {\mathbf {n} }}\cdot ({\vec {\mathbf {s} }}-{\vec {\mathbf {t} }}){\big )}{\hat {\mathbf {n} }}.$

And hence the equation for the reflected pair of vectors is,

${\vec {\mathbf {s} }}\,'={\vec {\mathbf {s} }}-2{\big (}{\hat {\mathbf {n} }}\cdot ({\vec {\mathbf {s} }}-{\vec {\mathbf {t} }}){\big )}{\hat {\mathbf {n} }},$

where ${\hat {\mathbf {n} }}$ is a unit vector normal to the plane. Obviously ${\vec {\mathbf {t} }}$ and ${\hat {\mathbf {n} }}$ are proportional, they differ only by scaling. Therefore, the equation can be written solely in terms of ${\vec {\mathbf {t} }}$,

${\vec {\mathbf {s} }}\,'={\vec {\mathbf {s} }}-2{\frac {{\vec {\mathbf {t} }}\cdot ({\vec {\mathbf {s} }}-{\vec {\mathbf {t} }})}{t^{2}}}{\vec {\mathbf {t} }},\quad t^{2}\equiv {\vec {\mathbf {t} }}\cdot {\vec {\mathbf {t} }}.$

Two consecutive reflections

PD Image
Fig. 3. Two reflections. Left drawing: 3-dimensional drawing. Right drawing: view along the PQ axis, drawing projected on the plane through ABC. This plane intersect the line PQ in the point P′

Two consecutive reflections in two intersecting planes give a rotation around the line of intersection. This is shown in Figure 3, where PQ is the line of intersection. The drawing on the left shows that reflection of point A in the plane through PMQ brings the point A to B. A consecutive reflection in the plane through PNQ brings B to the final position C. In the right-hand drawing it is shown that the rotation angle φ is equal to twice the angle between the mirror planes. Indeed, the angle ∠ AP'M = ∠ MP'B = α and ∠ BP'N = ∠ NP'C = β. The rotation angle ∠ AP'C ≡ φ = 2α + 2β and the angle between the planes is α+β = φ/2.

It is obvious that the product of two reflections is a rotation. Indeed, a reflection is an isometry and has determinant −1. The product of two isometric operators is again an isometry and the rule for determinants is det(AB) = det(A)det(B), so that the product of two reflections is an isometry with unit determinant, i.e., a rotation.

Let the normal of the first plane be ${\vec {\mathbf {s} }}$ and of the second ${\vec {\mathbf {t} }}$, then the rotation is represented by the matrix

$\left[\mathbf {E} -{\frac {2}{t^{2}}}{\vec {\mathbf {t} }}\otimes {\vec {\mathbf {t} }}\right]\,\left[\mathbf {E} -{\frac {2}{s^{2}}}{\vec {\mathbf {s} }}\otimes {\vec {\mathbf {s} }}\right]=\mathbf {E} -{\frac {2}{t^{2}}}{\vec {\mathbf {t} }}\otimes {\vec {\mathbf {t} }}-{\frac {2}{s^{2}}}{\vec {\mathbf {s} }}\otimes {\vec {\mathbf {s} }}+{\frac {4}{t^{2}s^{2}}}({\vec {\mathbf {t} }}\cdot {\vec {\mathbf {s} }})\;{\big (}{\vec {\mathbf {t} }}\otimes {\vec {\mathbf {s} }}{\big )}$

The (i,j) element if this matrix is equal to

$\delta _{ij}-{\frac {2t_{i}t_{j}}{t^{2}}}-{\frac {2s_{i}s_{j}}{s^{2}}}+{\frac {4t_{i}s_{j}(\sum _{k}t_{k}s_{k})}{t^{2}s^{2}}}.$

This formula is used in vector rotation.