Rotation matrix: Difference between revisions
imported>Paul Wormer |
imported>Paul Wormer |
||
| Line 5: | Line 5: | ||
where T stands for the [[transposed matrix]] and '''R'''<sup>−1</sup> is the [[inverse matrix| inverse]] of '''R'''. | where T stands for the [[transposed matrix]] and '''R'''<sup>−1</sup> is the [[inverse matrix| inverse]] of '''R'''. | ||
==Connection of orthogonal matrix to rotation== | ==Connection of orthogonal matrix to rotation== | ||
In general a motion of a rigid body (which is equivalent to an angle and distance preserving transformation of [[affine space]]) can be described as a translation of the body followed by a rotation. By a translation ''all'' points of the rigid body are displaced, while under a rotation at least one point stays in place. Let the the fixed point be ''O''. By [[Euler's theorem (rotation)|Euler's theorem]] follows that then not only the point is fixed but also an axis—the ''rotation axis''— through the fixed point. Write <math>\hat{n}</math> for the unit vector along the rotation axis and φ for the angle over which the body is rotated, then the rotation is written as <math> \mathcal{R}(\varphi, \hat{n}). </math> | In general a motion of a rigid body (which is equivalent to an angle and distance preserving transformation of [[affine space]]) can be described as a translation of the body followed by a rotation. By a translation ''all'' points of the rigid body are displaced, while under a rotation at least one point stays in place. Let the the fixed point be ''O''. By [[Euler's theorem (rotation)|Euler's theorem]] follows that then not only the point is fixed but also an axis—the ''rotation axis''— through the fixed point. Write <math>\hat{n}</math> for the unit vector along the rotation axis and φ for the angle over which the body is rotated, then the rotation operator on <math>\mathbb{R}^3</math> is written as <math> \mathcal{R}(\varphi, \hat{n}). </math> | ||
Erect three [[Cartesian coordinates|Cartesian coordinate]] axes with the origin in the fixed point ''O'' and take unit vectors <math>\hat{e}_x,\;\hat{e}_y,\;\hat{e}_z</math> along the axes, then the ''rotation matrix'' <math>\mathbf{R}(\varphi, \hat{n})</math> is defined by its elements | Erect three [[Cartesian coordinates|Cartesian coordinate]] axes with the origin in the fixed point ''O'' and take unit vectors <math>\hat{e}_x,\;\hat{e}_y,\;\hat{e}_z</math> along the axes, then the 3×3 ''rotation matrix'' <math>\mathbf{R}(\varphi, \hat{n})</math> is defined by its elements | ||
<math>R_{ji}(\varphi, \hat{n})</math> : | <math>R_{ji}(\varphi, \hat{n})</math> : | ||
| Line 22: | Line 22: | ||
Given a basis of a linear space, the association between a linear map and its matrix is one-to-one. | Given a basis of a linear space, the association between a linear map and its matrix is one-to-one. | ||
Since a rotation leaves angles and distances invariant, for any pair of vectors | Since a rotation <math>\mathcal{R}</math> (for convenience sake the rotation axis and angle are suppressed in the notation) leaves all angles and distances invariant, for any pair of vectors | ||
<math>\vec{a}</math> and <math>\vec{b}</math> in <math>\mathbb{R}^3</math> the [[inner product]] is invariant, | <math>\vec{a}</math> and <math>\vec{b}</math> in <math>\mathbb{R}^3</math> the [[inner product]] is invariant, that is, | ||
:<math> | :<math> | ||
\left(\mathcal{R}(\vec{a}),\;\mathcal{R}(\vec{b}) \right) = \left(\vec{a},\;\vec{b}\right). | \left(\mathcal{R}(\vec{a}),\;\mathcal{R}(\vec{b}) \right) = \left(\vec{a},\;\vec{b}\right). | ||
</math> | </math> | ||
A linear map with this property is called ''orthogonal''. It is easily shown that a similar vector-matrix relation holds. First we define | A linear map with this property is called ''orthogonal''. It is easily shown that a similar vector-matrix relation holds. First we define column vectors (stacked triplets of real numbers given in bold face): | ||
:<math> | :<math> | ||
\vec{a} =\left(\hat{e}_x,\;\hat{e}_y,\;\hat{e}_z\right)\begin{pmatrix}a_x\\a_y\\a_z\end{pmatrix} | \vec{a} =\left(\hat{e}_x,\;\hat{e}_y,\;\hat{e}_z\right)\begin{pmatrix}a_x\\a_y\\a_z\end{pmatrix} | ||
\ | \;\stackrel{\mathrm{def}}{=}\; \left(\hat{e}_x,\;\hat{e}_y,\;\hat{e}_z\right) \mathbf{a} | ||
\quad\hbox{and}\quad | \quad\hbox{and}\quad | ||
\vec{b} | \vec{b} | ||
=\left(\hat{e}_x,\;\hat{e}_y,\;\hat{e}_z\right)\begin{pmatrix}b_x\\b_y\\b_z\end{pmatrix} | =\left(\hat{e}_x,\;\hat{e}_y,\;\hat{e}_z\right)\begin{pmatrix}b_x\\b_y\\b_z\end{pmatrix} | ||
\ | \;\stackrel{\mathrm{def}}{=}\; \left(\hat{e}_x,\;\hat{e}_y,\;\hat{e}_z\right) \mathbf{b} | ||
</math> | </math> | ||
and observe that the inner product becomes by virtue of the orthonormality of the basis vectors | and observe that the inner product becomes by virtue of the orthonormality of the basis vectors | ||
| Line 41: | Line 41: | ||
\left(a_x,\;a_y,\;a_z\right) \begin{pmatrix}b_x\\b_y\\b_z\end{pmatrix} \equiv a_xb_x+a_yb_y+a_zb_z. | \left(a_x,\;a_y,\;a_z\right) \begin{pmatrix}b_x\\b_y\\b_z\end{pmatrix} \equiv a_xb_x+a_yb_y+a_zb_z. | ||
</math> | </math> | ||
The invariance of the inner product under <math>\mathcal{R}</math> leads to | The invariance of the inner product under the rotation operator <math>\mathcal{R}</math> leads to | ||
:<math> | :<math> | ||
\big(\mathbf{R}\mathbf{a}\big)^\mathrm{T}\; \mathbf{R}\mathbf{b} = | \big(\mathbf{R}\mathbf{a}\big)^\mathrm{T}\; \mathbf{R}\mathbf{b} = | ||
| Line 57: | Line 57: | ||
A matrix with this property is called ''orthogonal''. So, a rotation gives rise to a unique orthogonal matrix. | A matrix with this property is called ''orthogonal''. So, a rotation gives rise to a unique orthogonal matrix. | ||
Conversely, consider | Conversely, consider an arbitrary point ''P'' in the body and let the vector <font style="vertical-align: text-bottom"> <math>\overrightarrow{OP}</math></font> connect the fixed point ''O'' with ''P''. Expressing this vector with respect to a Cartesian frame in ''O'' gives the column vector '''p''' (three stacked real numbers). Multiply '''p''' by the orthogonal matrix '''R''', then '''p'''′ = '''R'''<b>p</b> represents the rotated point ''P''′ (or, more precisely, the vector <font style="vertical-align: text-bottom"> <math>\overrightarrow{OP'}</math></font> is represented by column vector '''p'''′ with respect to the ''same'' Cartesian frame). If we map all points ''P'' of the body by the same matrix '''R''' in this manner, we have rotated the body. Thus, an orthogonal matrix leads to a unique rotation. Note that the Cartesian frame is fixed here and that points of the body are rotated, this is known as an ''active'' rotation. Instead, the rigid body could have been left invariant and the Cartesian frame could have been rotated, this also leads to new column vectors of the form '''p'''′ ≡ '''R'''<b>p</b>, such rotations are called ''passive''. | ||
==Properties of orthogonal matrix== | ==Properties of orthogonal matrix== | ||
Writing out matrix products it follows that both the rows and the columns of the matrix are orthonormal (normalized and orthogonal). Indeed, | Writing out matrix products it follows that both the rows and the columns of the matrix are orthonormal (normalized and orthogonal). Indeed, | ||
Revision as of 02:28, 21 May 2009
In mathematics and physics a rotation matrix is synonymous with a 3×3 orthogonal matrix, which is a matrix R satisfying
where T stands for the transposed matrix and R−1 is the inverse of R.
Connection of orthogonal matrix to rotation
In general a motion of a rigid body (which is equivalent to an angle and distance preserving transformation of affine space) can be described as a translation of the body followed by a rotation. By a translation all points of the rigid body are displaced, while under a rotation at least one point stays in place. Let the the fixed point be O. By Euler's theorem follows that then not only the point is fixed but also an axis—the rotation axis— through the fixed point. Write for the unit vector along the rotation axis and φ for the angle over which the body is rotated, then the rotation operator on is written as
Erect three Cartesian coordinate axes with the origin in the fixed point O and take unit vectors along the axes, then the 3×3 rotation matrix is defined by its elements :
In a more condensed notation this equation can be written as
Given a basis of a linear space, the association between a linear map and its matrix is one-to-one.
Since a rotation (for convenience sake the rotation axis and angle are suppressed in the notation) leaves all angles and distances invariant, for any pair of vectors and in the inner product is invariant, that is,
A linear map with this property is called orthogonal. It is easily shown that a similar vector-matrix relation holds. First we define column vectors (stacked triplets of real numbers given in bold face):
and observe that the inner product becomes by virtue of the orthonormality of the basis vectors
The invariance of the inner product under the rotation operator leads to
since this holds for any pair a and b it follows that a rotation matrix satisfies
where E is the 3×3 identity matrix. For finite-dimensional matrices one shows easily
A matrix with this property is called orthogonal. So, a rotation gives rise to a unique orthogonal matrix.
Conversely, consider an arbitrary point P in the body and let the vector connect the fixed point O with P. Expressing this vector with respect to a Cartesian frame in O gives the column vector p (three stacked real numbers). Multiply p by the orthogonal matrix R, then p′ = Rp represents the rotated point P′ (or, more precisely, the vector is represented by column vector p′ with respect to the same Cartesian frame). If we map all points P of the body by the same matrix R in this manner, we have rotated the body. Thus, an orthogonal matrix leads to a unique rotation. Note that the Cartesian frame is fixed here and that points of the body are rotated, this is known as an active rotation. Instead, the rigid body could have been left invariant and the Cartesian frame could have been rotated, this also leads to new column vectors of the form p′ ≡ Rp, such rotations are called passive.
Properties of orthogonal matrix
Writing out matrix products it follows that both the rows and the columns of the matrix are orthonormal (normalized and orthogonal). Indeed,
where δij is the Kronecker delta.
Orthogonal matrices come in two flavors: proper (det = 1) and improper (det = −1) rotations. Indeed, invoking some properties of determinants, one can prove
Compact notation
A compact way of presenting the same results is the following. Designate the columns of R by r1, r2, r3, i.e.,
- .
The matrix R is orthogonal if
The matrix R is a proper rotation matrix, if it is orthogonal and if r1, r2, r3 form a right-handed set, i.e.,
Here the symbol × indicates a cross product and is the antisymmetric Levi-Civita symbol,
and if two or more indices are equal.
The matrix R is an improper rotation matrix if its column vectors form a left-handed set, i.e.,
The last two equations can be condensed into one equation
by virtue of the the fact that the determinant of a proper rotation matrix is 1 and of an improper rotation −1. This was proved above, an alternative proof is the following: The determinant of a 3×3 matrix with column vectors a, b, and c can be written as scalar triple product
- .
It was just shown that for a proper rotation the columns of R are orthonormal and satisfy,
Likewise the determinant is −1 for an improper rotation.
Explicit expression
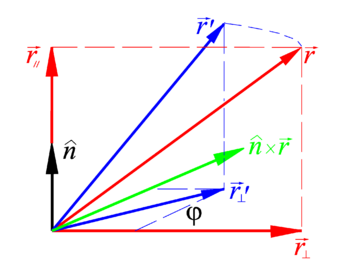
Let be a vector pointing from the fixed point O of a rotating rigid body to an arbitrary point P of the body. A rotation of this arbitrary vector around the unit vector over an angle φ can be written as
where • indicates an inner product and the symbol × a cross product.

































![{\displaystyle {\mathcal {R}}(\varphi ,{\hat {n}})({\vec {r}}\,)={\vec {r}}\,'=\left[{\vec {r}}-({\hat {n}}\cdot {\vec {r}}\,)\;{\hat {n}}\right]\cos \varphi +({\hat {n}}\times {\vec {r}}\,)\sin \varphi .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a88af8807050b97725474050c21f7a28a8d096ce)