Rotation matrix

In mathematics and physics a rotation matrix is synonymous with a 3×3 orthogonal matrix, which is a matrix R satisfying

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{R}^\mathrm{T} = \mathbf{R}^{-1}, }

where T stands for the transposed matrix and R⁻¹ is the inverse of R.

Connection of orthogonal matrix to rotation

In general a motion of a rigid body (which is equivalent to an angle and distance preserving transformation of affine space) can be described as a translation of the body followed by a rotation. By a translation all points of the rigid body are displaced, while under a rotation at least one point stays in place. Let the the fixed point be O. By Euler's theorem follows that then not only the point is fixed but also an axis—the rotation axis— through the fixed point. Write Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{n}} for the unit vector along the rotation axis and φ for the angle over which the body is rotated, then the rotation operator on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^3} is written as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{R}(\varphi, \hat{n}). }

Erect three Cartesian coordinate axes with the origin in the fixed point O and take unit vectors Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{e}_x,\;\hat{e}_y,\;\hat{e}_z} along the axes, then the 3×3 rotation matrix Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{R}(\varphi, \hat{n})} is defined by its elements Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{ji}(\varphi, \hat{n})}  :

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{R}(\varphi, \hat{n})(\hat{e}_i) = \sum_{j=x,y,x} \hat{e}_j R_{ji}(\varphi, \hat{n}) \quad\hbox{for}\quad i=x,y,z. }

In a more condensed notation this equation can be written as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{R}(\varphi, \hat{n})\left(\hat{e}_x,\;\hat{e}_y,\;\hat{e}_z\right) = \left(\hat{e}_x,\;\hat{e}_y,\;\hat{e}_z\right) \; \mathbf{R}(\varphi, \hat{n}). }

Given a basis of a linear space, the association between a linear map and its matrix is one-to-one.

Since a rotation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{R}} (for convenience sake the rotation axis and angle are suppressed in the notation) leaves all angles and distances invariant, for any pair of vectors Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{a}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{b}} in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^3} the inner product is invariant, that is,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\mathcal{R}(\vec{a}),\;\mathcal{R}(\vec{b}) \right) = \left(\vec{a},\;\vec{b}\right). }

A linear map with this property is called orthogonal. It is easily shown that a similar vector-matrix relation holds. First we define column vectors (stacked triplets of real numbers given in bold face):

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{a} =\left(\hat{e}_x,\;\hat{e}_y,\;\hat{e}_z\right)\begin{pmatrix}a_x\\a_y\\a_z\end{pmatrix} \;\stackrel{\mathrm{def}}{=}\; \left(\hat{e}_x,\;\hat{e}_y,\;\hat{e}_z\right) \mathbf{a} \quad\hbox{and}\quad \vec{b} =\left(\hat{e}_x,\;\hat{e}_y,\;\hat{e}_z\right)\begin{pmatrix}b_x\\b_y\\b_z\end{pmatrix} \;\stackrel{\mathrm{def}}{=}\; \left(\hat{e}_x,\;\hat{e}_y,\;\hat{e}_z\right) \mathbf{b} }

and observe that the inner product becomes by virtue of the orthonormality of the basis vectors

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left( \vec{a},\; \vec{b} \right) = \mathbf{a}^\mathrm{T} \mathbf{b}\equiv \left(a_x,\;a_y,\;a_z\right) \begin{pmatrix}b_x\\b_y\\b_z\end{pmatrix} \equiv a_xb_x+a_yb_y+a_zb_z. }

The invariance of the inner product under the rotation operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{R}} leads to

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \big(\mathbf{R}\mathbf{a}\big)^\mathrm{T}\; \mathbf{R}\mathbf{b} = \mathbf{a}^\mathrm{T} \mathbf{R}^\mathrm{T}\; \mathbf{R}\mathbf{b} }

since this holds for any pair a and b it follows that a rotation matrix satisfies

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{R}^\mathrm{T} \mathbf{R} = \mathbf{E} }

where E is the 3×3 identity matrix. For finite-dimensional matrices one shows easily

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{R}^\mathrm{T} \mathbf{R} = \mathbf{E} \quad \Longleftrightarrow\quad\mathbf{R}\mathbf{R}^\mathrm{T} = \mathbf{E}. }

A matrix with this property is called orthogonal. So, a rotation gives rise to a unique orthogonal matrix.

Conversely, consider an arbitrary point P in the body and let the vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{OP}} connect the fixed point O with P. Expressing this vector with respect to a Cartesian frame in O gives the column vector p (three stacked real numbers). Multiply p by the orthogonal matrix R, then p′ = Rp represents the rotated point P′ (or, more precisely, the vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{OP'}} is represented by column vector p′ with respect to the same Cartesian frame). If we map all points P of the body by the same matrix R in this manner, we have rotated the body. Thus, an orthogonal matrix leads to a unique rotation. Note that the Cartesian frame is fixed here and that points of the body are rotated, this is known as an active rotation. Instead, the rigid body could have been left invariant and the Cartesian frame could have been rotated, this also leads to new column vectors of the form p′ ≡ Rp, such rotations are called passive.

Properties of orthogonal matrix

Writing out matrix products it follows that both the rows and the columns of the matrix are orthonormal (normalized and orthogonal). Indeed,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \mathbf{R}^\mathrm{T} \mathbf{R} &= \mathbf{E} \quad\Longrightarrow\quad \sum_{k=1}^{3} R_{ki}\, R_{kj} =\delta_{ij} \quad\hbox{(columns)} \\ \mathbf{R} \mathbf{R}^\mathrm{T} &= \mathbf{E} \quad\Longrightarrow\quad \sum_{k=1}^{3} R_{ik}\, R_{jk} =\delta_{ij} \quad\hbox{(rows)} \\ \end{align} }

where δ_ij is the Kronecker delta.

Orthogonal matrices come in two flavors: proper (det = 1) and improper (det = −1) rotations. Indeed, invoking some properties of determinants, one can prove

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1=\det(\mathbf{E})=\det(\mathbf{R}^\mathrm{T}\mathbf{R}) = \det(\mathbf{R}^\mathrm{T})\det(\mathbf{R}) = \det(\mathbf{R})^2 \quad\Longrightarrow \quad \det(\mathbf{R}) = \pm 1. }

Compact notation

A compact way of presenting the same results is the following. Designate the columns of R by r₁, r₂, r₃, i.e.,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{R} = \left(\mathbf{r}_1,\, \mathbf{r}_2,\, \mathbf{r}_3 \right) } .

The matrix R is orthogonal if

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}_i^\mathrm{T} \mathbf{r}_j \equiv \mathbf{r}_i \cdot \mathbf{r}_j = \delta_{ij}, \quad i,j = 1,2,3 . }

The matrix R is a proper rotation matrix, if it is orthogonal and if r₁, r₂, r₃ form a right-handed set, i.e.,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}_i \times \mathbf{r}_j = \sum_{k=1}^3 \, \varepsilon_{ijk} \mathbf{r}_k . }

Here the symbol × indicates a cross product and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon_{ijk}} is the antisymmetric Levi-Civita symbol,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \varepsilon_{123} =&\; \varepsilon_{312} = \varepsilon_{231} = 1 \\ \varepsilon_{213} =&\; \varepsilon_{321} = \varepsilon_{132} = -1 \end{align} }

and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon_{ijk} = 0} if two or more indices are equal.

The matrix R is an improper rotation matrix if its column vectors form a left-handed set, i.e.,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}_i \times \mathbf{r}_j = - \sum_{k=1}^3 \, \varepsilon_{ijk} \mathbf{r}_k \; . }

The last two equations can be condensed into one equation

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}_i \times \mathbf{r}_j = \det(\mathbf{R}) \sum_{k=1}^3 \; \varepsilon_{ijk} \mathbf{r}_k }

by virtue of the the fact that the determinant of a proper rotation matrix is 1 and of an improper rotation −1. This was proved above, an alternative proof is the following: The determinant of a 3×3 matrix with column vectors a, b, and c can be written as scalar triple product

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \det\left(\mathbf{a},\,\mathbf{b},\, \mathbf{c}\right) = \mathbf{a} \cdot (\mathbf{b}\times\mathbf{c}) } .

It was just shown that for a proper rotation the columns of R are orthonormal and satisfy,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}_1 \cdot (\mathbf{r}_2 \times \mathbf{r}_3 ) = \mathbf{r}_1 \cdot\left(\sum_{k=1}^3 \, \varepsilon_{23k} \, \mathbf{r}_k \right) = \varepsilon_{231} = 1 . }

Likewise the determinant is −1 for an improper rotation.

Explicit expression

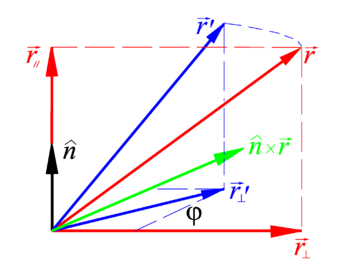
Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{OP} \equiv \vec{r}} be a vector pointing from the fixed point O of a rotating rigid body to an arbitrary point P of the body. A rotation of this arbitrary vector around the unit vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{n}} over an angle φ can be written as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{R}(\varphi, \hat{n})(\vec{r}\,) = \vec{r}\,' =\left[ \vec{r} -(\hat{n}\cdot\vec{r}\,)\; \hat{n}\right] \cos\varphi + (\hat{n} \times \vec{r}\,) \sin\varphi. }

where • indicates an inner product and the symbol × a cross product.

Rotation of vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \vec{r}} around axis Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \hat{n}} over an angle φ. The red vectors are in the plane of drawing spanned by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \vec{r}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \hat{n}} . The blue vectors are rotated, the green cross product points away from the reader and is perpendicular to the plane of drawing.